
Using Dominated Solutions to the Uniformity of Non-dominated
Solution Distributions in NSGA-II
Kina Yokoyama and Yuji Sato
Faculty of Computer and Information Sciences, Hosei University, 3-7-2 Kajino-cho Koganei-shi, Tokyo, Japan
Keywords: Multi-objective Optimization, NSGA-II, Non-dominated Sorting, Pareto Optimal Front, Dominated Solution.
Abstract: This paper proposes a method for improving the diversity of the Pareto front in a fast elitist non-dominated
sorting genetic algorithm (NSGA-II), which is an evolutionary multi-objective optimization algorithm.
Conventional NSGA-II has excellent convergence to the Pareto front, but it has been reported that for some
test cases, it does not produce a more diverse solution distribution than the strength Pareto evolutionary
algorithm 2 (SPEA2). To avoid this problem, we propose a method that stores an archive of dominated
solutions that may be effective in improving diversity in the conventional search process when used for
genetic operations. We experimentally compare this approach with the conventional method on the typical
multi-objective test problems ZDT1, ZDT2, and ZDT3. By evaluating the performance based on Pareto front
diagrams and hypervolume values, we show that the proposed method is effective at improving the diversity
at both ends of Pareto optimal front and the uniformity of the solution distribution.
1 INTRODUCTION
Many real-world optimization problems have
multiple objectives. These objectives often have
trade-off relationships, and there is no single solution
that is optimal for all objective functions. It is
therefore important to have some way of accurately
locating the curved surface (Pareto optimal front)
formed by the set of Pareto optimal solutions.
Evolutionary multi-objective optimization
algorithms, which are based on evolutionary
computation, are being researched as a way of
tackling this problem (Carlos, 2006), due to their
ability to find a set of solutions that approximate the
Pareto optimal front by running a single algorithm,
and due to the breadth of optimal solutions they are
able to find. In this paper, we focus on a fast elitist
non-dominated sorting genetic algorithm (NSGA-II)
(Deb, 2002), which is the most practical of these
algorithms. The main characteristics of the NSGA-II
algorithm are its fast non-dominated sort, which
improves convergence to the Pareto optimal front,
and the crowding sort for uniform solution
distribution.
On the other hand, compared with the strength
Pareto evolutionary algorithm 2 (SPEA2) (Zitzler,
2001), which focuses on the dominance of solutions
and the preservation of non-dominated solutions as in
NSGA-II, it has been reported that although it
achieves better convergence on the Pareto front, there
are test cases where it did not achieve superiority in
terms of the diversity of the solution distribution. If
the solution distribution does not have sufficient
diversity, this could be due to a bias in the decision
maker’s choice of final solutions. In this paper, we
address this problem by proposing a method that
improves the uniformity of the solution distribution
by using an archive population to preserve some of
the inferior solutions that are usually culled at the start
of a new generation but which may be effective at
improving the diversity of the population, and by
actively using these inferior solutions in genetic
operations.
2 CONVENTIONAL METHODS
2.1 Overview of NSGA-II
As shown in Equations (1), a constrained multi-
objective optimization problem involves minimizing
(or maximizing) k different objective functions f
based on m different inequality constraints g.
212
Yokoyama, K. and Sato, Y.
Using Dominated Solutions to the Uniformity of Non-dominated Solution Distributions in NSGA-II.
DOI: 10.5220/0010143502120219
In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 212-219
ISBN: 978-989-758-475-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
,
,
…,
1,2,…,
,
,
…,
0
1,2,…,
(1)
Since there are trade-off relationships between the
objectives functions, studies are being made to find
the Pareto optimal front by means of evolutionary
computation. A typical evolutionary multi-objective
optimization algorithm is NSGA-II, which was
proposed by Deb et al. in 2000 as an improved version
of the non-dominated sorting genetic algorithm
(NSGA) (Srinivas, 1994). It searches for solutions by
using a combination of fast non-dominated sort,
crowding sort, and crowded tournament selection.
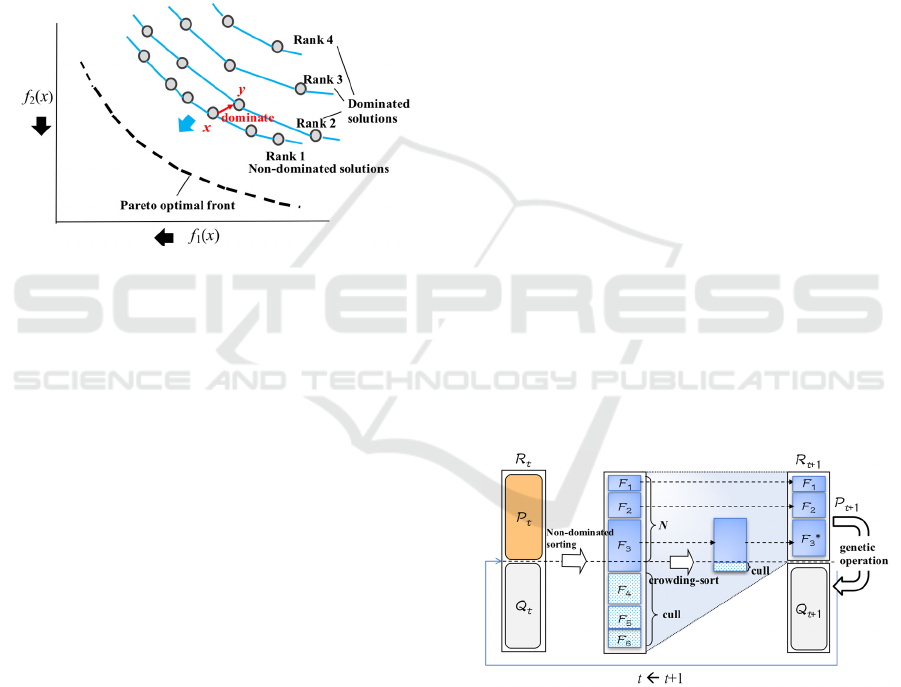
Figure 1: Conceptual illustration of a fast dominated sort.
Figure 1 shows a conceptual illustration of a fast
dominated sort. A fast non-dominated sort is an
operation that classifies all individuals by rank,
focusing on the dominated/non-dominated
relationships between individuals. For example, in a
minimization problem, a solution candidate
(individual) x is defined as dominating y when the
following Equation (2) is satisfied:
∀
∧∃
(2)
Using this definition, we can rank each individual
by ascertaining the dominated/non-dominated
relationships between each individual. First, we
determine the individuals that belong to the best Rank
1 group. For each individual, count the number of
other individuals that it dominates, and the number of
other individuals by which it is dominated. If it is not
dominated by any other individual, then it is deemed
to be a non-dominated solution and is placed in Rank
1. The other individuals are dominated solutions.
Next, the Rank 1 individuals are ignored and the
dominated/non-dominated definitions are used to
determine Rank 2 individuals under the same
conditions as when determining the Rank 1
individuals. A fast non-dominated sort is achieved by
repeating this operation until all the individuals have
been ranked.
Crowding sort is a method that determines
superiority/inferiority relationships between entities
at the same rank based on their crowding distance. An
individual’s crowding distance is the sum of the
distances to its two neighbouring individuals on the
Pareto front in the objective function space. A larger
crowding distance (i.e., a solution that is less
crowded) is ranked with higher precedence. In a
crowded tournament selection, the solution
candidates are first ranked by a fast non-dominated
sort, and then the candidates of equal rank are sorted
by crowding distance.
Figure 2 shows a conceptual illustration of how
the population is updated in a crowded tournament
selection. NSGA-II advances the solution search by
using an archive population P
t
that stores non-
dominated solutions as the parent population, and the
initial search population Q
t
for performing the search
as the child population. First, generate a group R
t
= P
t
∪ Q
t
that combines the parent population P
t
and the
child population Q
t
. This group R
t
is first subjected to
a non-dominated sort to rank each solution candidate.
In the figure, F
n
represents a solution candidate group
of rank n. Next, perform a crowding sort and select
the top N individuals with the highest number from
the 2N individuals R
t
as P
t+1
. The parent individuals
selected from P
t+1
are then crossed over and
genetically manipulated by mutation to generate a
new child population Q
t+1
. These operations
constitute one generation step, and these generation
steps are repeated the specified number of times.
Figure 2: Creating a new population generation by crowded
tournament selection.
2.2 Problems with Conventional
Methods
Figure 3 shows an example of the state diagram of a
population R
t
that is considered to lead to a decrease
in the diversity of the solution distribution. The non-
dominant sort used in NSGA-II is an operation that
Using Dominated Solutions to the Uniformity of Non-dominated Solution Distributions in NSGA-II
213
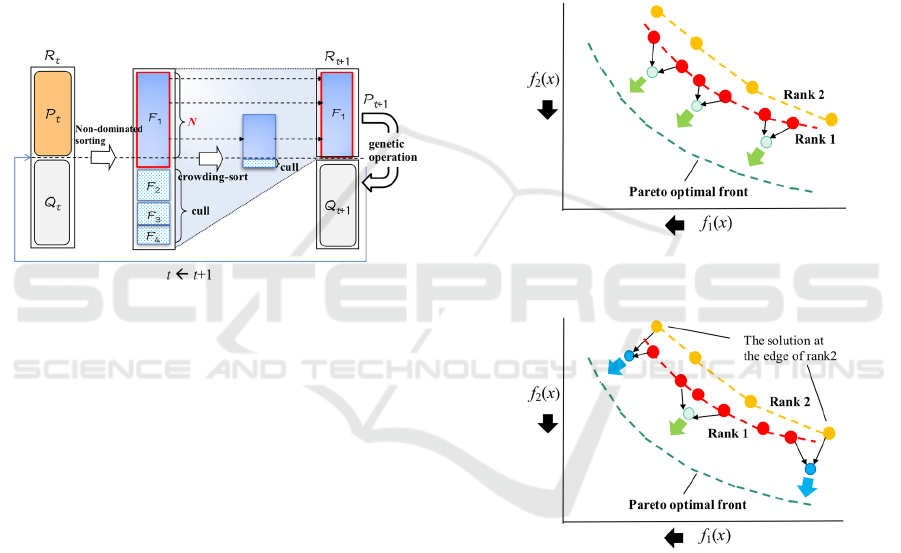
classifies all individuals into several ranks by
focusing on the dominated/non-dominated
relationships between individuals. Here, the best
solution group is defined as Rank 1, followed in turn
by Rank 2 and Rank 3. For some problems, these
dominated/non-dominated solution relationships may
cease to hold as the number of generations increases.
In such cases, all N individuals selected for the
archive population Pt+1 would become Rank 1
solutions, while the other solutions of Rank 2, Rank
3, etc. obtained in the previous solution search would
be completely eliminated. In this study, we consider
that one of the reasons why NSGA-II sometimes has
inferior solution diversity compared with SPEA2 is
the lack of solutions of other ranks besides Rank 1 at
the initial stages of the search.
Figure 3: Example of the state diagram of population R
t
where all the archive groups are of Rank 1.
3 PROPOSAL OF GENETIC
OPERATION USING
DOMINATED SOLUTIONS
3.1 Genetic Manipulation using
Dominated Solutions
In this paper, we propose a method applied to genetic
operations that involves preserving some of the
inferior solutions that are culled in conventional
search processes but may be capable of leading to
improved diversity. For example, the solutions at both
ends of the Rank 2 solution distribution could be
preserved. By preserving the solutions at both ends of
the Rank 2 solution distribution in the archive
population and using them for genetic manipulation,
it may be possible to improve the diversity of the next
generation of solutions. Figure 4 shows an example
of a solution distribution diagram generated by
performing genetic operations only on Rank 1
solutions using the two-objective maximization
problem as an example. On the other hand, Fig. 5
shows an example of a solution distribution diagram
generated by performing genetic operations
according to the proposed method. In the
conventional genetic operations shown in Fig. 4, the
individuals represented by green circles are generated
from Rank 1 parent individuals. Although this
improves the convergence to the true Pareto front, it
also reduces the breadth (i.e., diversity) of the
solution distribution. In the proposed method shown
in Fig. 5, the genetic operations also include inferior
solutions at both ends of the Rank 2 solution
distribution. As indicated by the blue circles in the
figure, these individuals should help to improve the
breadth of the solution distribution.
Figure 4: Searching for a solution using only Rank 1
solutions.
Figure 5: Including Rank 2 solutions for greater solution
diversity.
3.2 Replacement with Archived
Dominated Solutions
Figure 6 summarizes the method used to replace
solutions in P
t
, when preserving the solutions at both
ends of the Rank 2 solution distribution in the archive
population. In the conventional method, the
population number N is determined as an initial
parameter, and genetic operations such as crossovers
and mutations are performed among the archive
population of N individuals. However, if the proposed
method is implemented by simply adding inferior
ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications
214
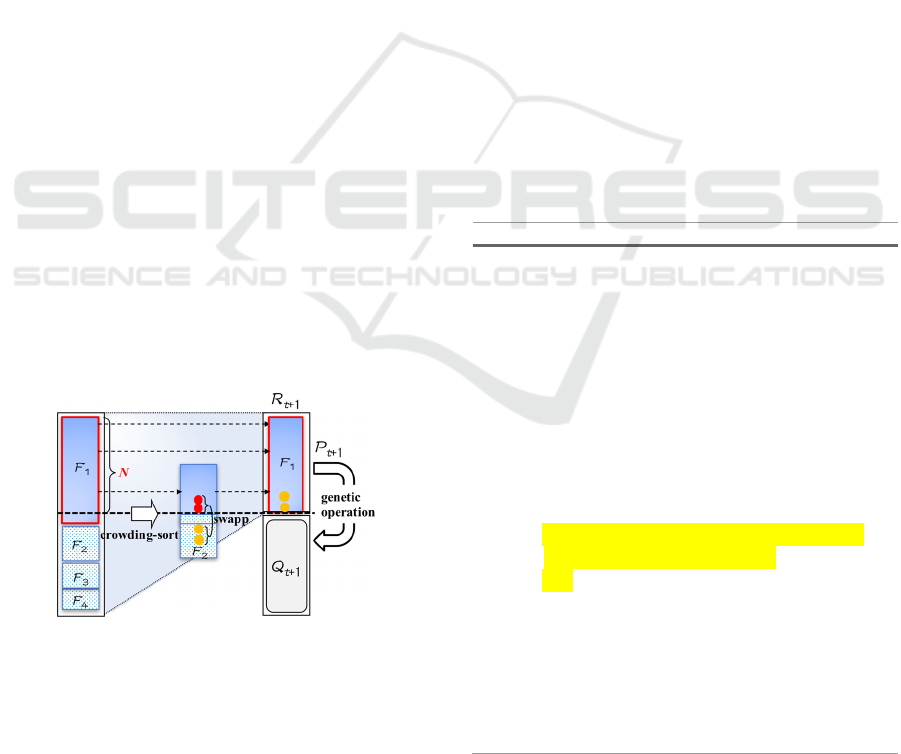
solutions to this archive population before performing
genetic operations, this would result in operations
being performed on N+2 individuals instead of N
individuals. The use of a larger number of parent
individuals are used in the generation of a solution
would confer advantages in terms of the speed of
convergence and the diversity of the solution, making
it difficult to make a fair comparison with the
conventional method. Therefore, in this study, the top
two solutions in the Rank 2 solution set preserved in
the archive population replace the lowest-ranked
Rank 1 solutions that would originally have been
selected for the N archive populations. Since the
solutions belonging to Rank 1 are sorted based on
their crowding distance, the two solutions with the
smallest crowding distance (i.e., the most densely
distributed solutions) in Rank 1 are replaced. This
replacement maintains a constant number of
individuals N, and allows genetic operations to be
performed without changing the conditions that apply
between individuals of the archive population defined
by N.
Here, the two lowest-ranked solutions in Rank 1
are often clustered around the central part that is
distant from both ends of the current Pareto front. By
deleting these solutions and replacing them with the
solutions at both ends of Rank 2, it is therefore less
likely that genetic manipulation will be performed in
places where there is a high density of solution
candidates, and it will be more likely that solution
candidates will be generated at both ends of the Pareto
front in the next generation. In other words, this
approach is effective at improving the uniformity of
the solution distribution when the Pareto front of the
next generation is viewed as a whole.
Figure 6: Replacement of inferior solutions.
(Sato, 2007) has proposed the method that
introduces variables for controlling the dominance
area of the solutions to correct the individuals stored
in the archive population. Although the same effect as
the proposal of this method can be expected by setting
an appropriate parameter value, the appropriate value
of the control parameter cannot be known until after
the solution search. Since it constantly changes
during the search process, there is a problem that it is
difficult to determine an appropriate control
parameter value in advance. On the other hand, the
method proposed here can be realized with a slight
modification to the original NSGA-II program.
3.3 Event-driven Replacement of
Solution Candidates
The pseudo code of the proposed method is
summarized in Figure 7. The colored parts
correspond to the modifications made in the proposed
method. In this paper, although our aim is to improve
the diversity and uniformity of the solution
distribution, it is also important to consider the search
efficiency and convergence. If the proposed method
is executed in all evaluation generations, it could lead
to worse convergence on the Pareto optimal front than
the conventional method. Therefore, instead of
applying the proposed method at every generation,
we use a branching condition to switch to the
conventional method when all N individuals selected
for archive population P
t+1
are Rank 1 solutions, i.e.,
when dominated/non-dominated relationships are not
established in archive population P
t+1
.
Algorithm 1. Pseudo code of the proposed method.
// t: number of generations
// P(t): archive population of size N
// Q(t): search population of size N
// F
i
: solution set of rank i
1 t = 0;
2 Generate P(t); // generate initial population
3 Generate Q(t); // by applying genetic
operations to P(t);
4 R(t) P(t) ∪ Q(t);
5 Until S
TOPPING
C
ONDITION
do
6 Apply non-dominated sort to R(t);
7 Apply crowding sort to R(t);
8 if | F
i
| ≥ N then replacing to archive the
edge of dominated solutions;
9 end
10 selection; // archive the top N
individuals to P(t) and cull the
remaining individuals
11 Generate Q(t); // by applying genetic
operations to P(t);
12 t t + 1;
13 end
Figure 7: The pseudo code of the proposed method.
Using Dominated Solutions to the Uniformity of Non-dominated Solution Distributions in NSGA-II
215

4 EVALUATION
4.1 Experimental Method
We performed an experimental comparison of the
proposed algorithm with the conventional NSGA-II
algorithm using ZDT1, ZDT2, and ZDT3 (Deb,
2002), which are typical test functions for multi-
objective optimization problems. ZDT1 has a convex
Pareto optimal front and is suitable for evaluating
convergence. It is defined by the following equations:
・
19
・
1
1
/
(4)
where
∈0,1, 2,…,, 30.
ZDT2 has a concave Pareto-optimal front and is
suitable for evaluating diversity. It is defined by the
following equations:
・
19
・
1
1
/
(5)
where
∈0,1, 2,…,, 30.
ZDT3 is a complicated problem characterized by
a discontinuous Pareto optimal front, and is defined
by the following equations:
・
19
・
1
1
/
/
・
10
(6)
where
∈0,1, 2,…,, 30.
We evaluated the proposed method using these
three test problems, focusing on the comparison of the
solution distribution diagram with that of the
conventional method. In addition, since ZDT1 is
characterized by a tendency to converge on the Pareto
optimal front within a small number of generations,
we focused on the transition of hypervolume (HV)
values (Beume, 2009) and to check whether or not the
proposed method adversely affects the convergence.
On the other hand, ZDT2 is characterized by the ease
with which it is possible to confirm the breadth of
solutions as the number of generations increases, so
we regarded this as a useful way of confirming the
effects of the proposed method on the breadth of the
solution distribution. Here, HV is an index
representing the overall effectiveness of the solution
distribution, and is defined as the volume (or, in the
case of two objectives, the surface area) of the
hyperplane formed by the origin and the finally
obtained Pareto front. The definition of HV can be
expressed as shown in Equation (7) In Eq. (4), n
PF
represents the number of solutions in the Pareto set,
and v
i
represents the hypercube for each solution i
from the origin.
volume∪
(7)
In the experiment, we compared and studied the
following three items:
Uniformity of the solution distribution in Pareto
front diagrams;
The number of non-inferior solutions generated at
both ends of the Pareto front;
The relationship between the number of
generations and the HV value;
Table 1 shows the GA parameters used in all the
test questions and the origin point used for the
calculation of HV values.
Table 1: GA parameters and origin point.
Population size 20, 100
Max. number of generations 1000
Crossover method 2-point crossover
Crossover rate 0.9
Mutation method Polynomial mutation
Mutation rate 0.033
Reference point (1.2, 1.5)
4.2 Experimental Results and
Discussion
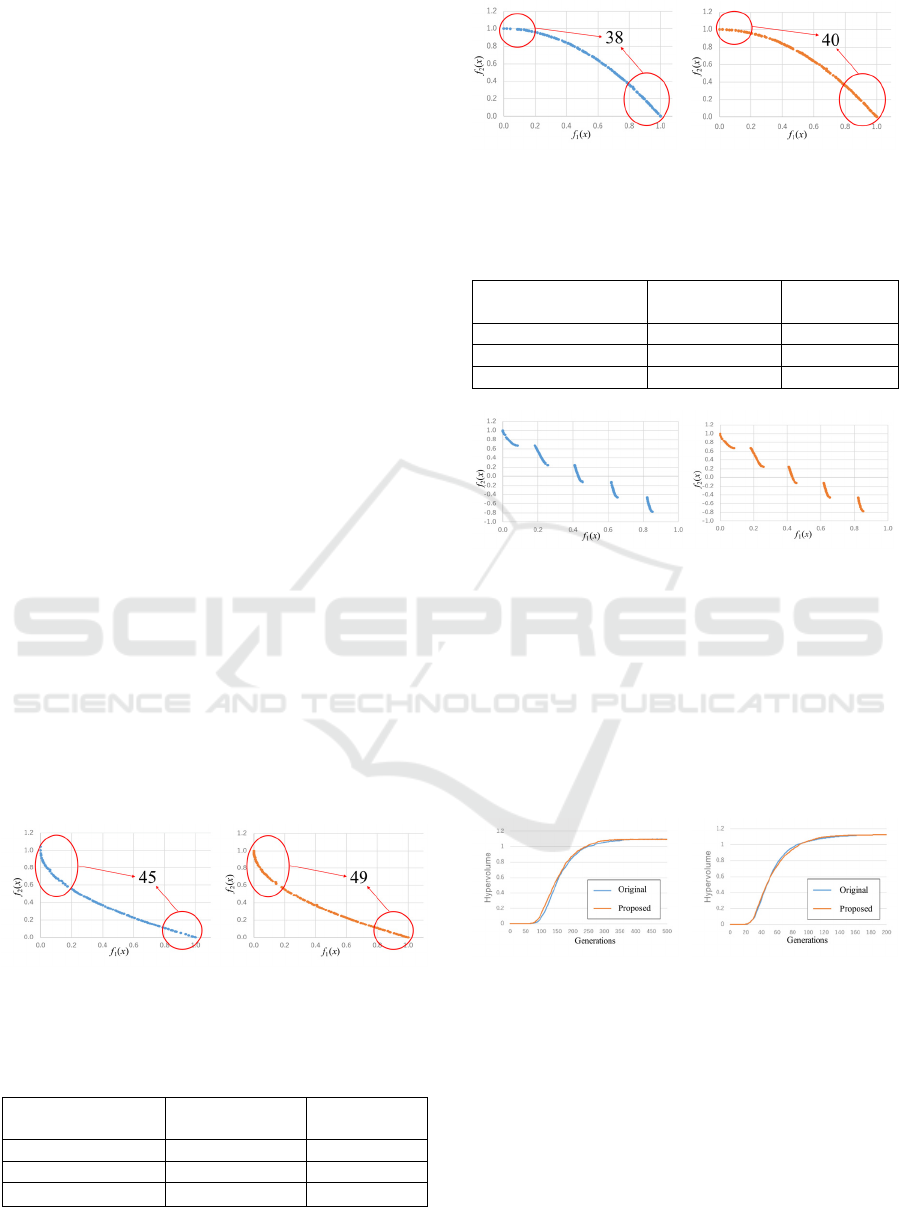
Figures 8 through 10 compare the Pareto front
diagrams obtained for a population size of 20 when
the test problems are applied to the conventional
method and the proposed method. Similarly, Figs. 11
through 13 compare the Pareto front diagrams for
population size of 100. In Figs. 8, 9, 11 and 12, the
red circles and arrows indicate the numbers of non-
inferior solutions in order to confirm the extent to
ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications
216
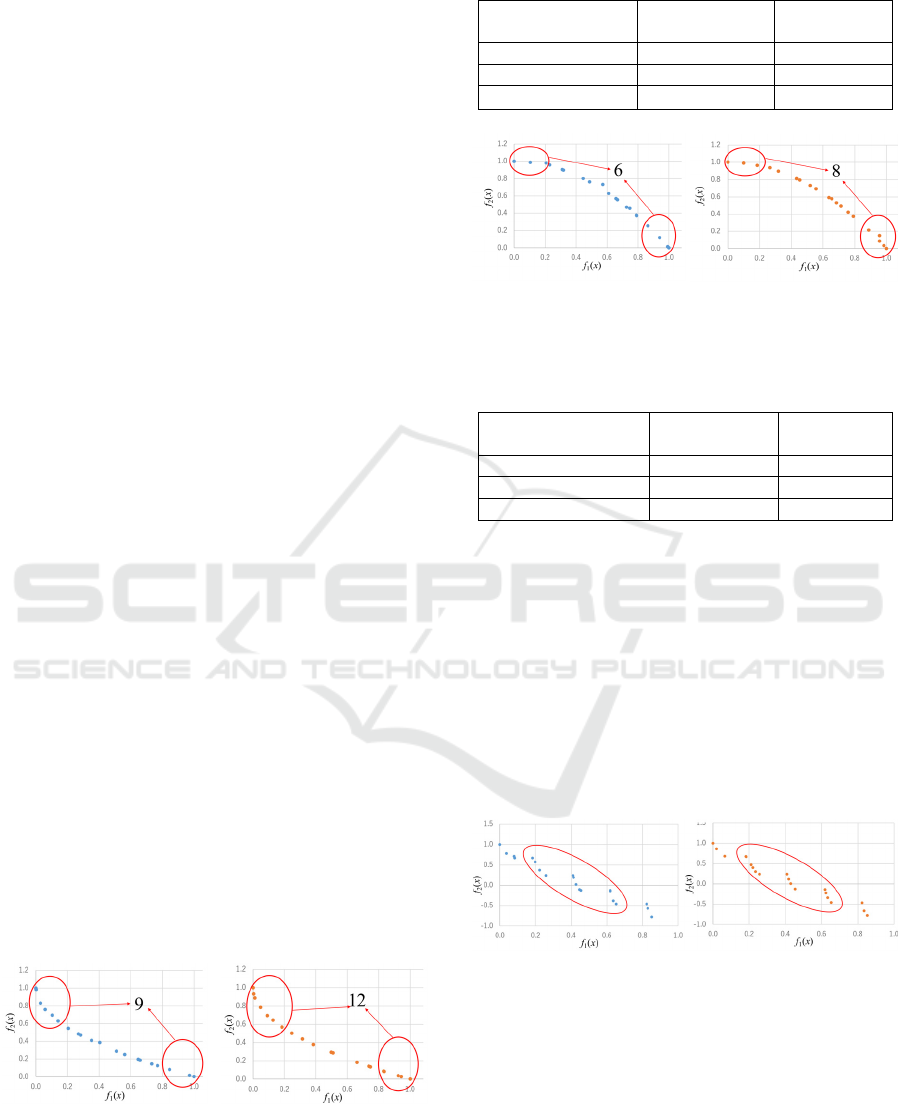
which the number of solutions generated at the ends
of the Pareto curve is increased.
Tables 2 through 5 summarize the number of
individuals corresponding to non-inferior solutions
generated at both ends of the Pareto fronts for ZDT1
and ZDT2. Since the Pareto front is discontinuous in
ZDT3, the table is omitted, and we instead consider
the diversity and uniformity of the overall solution
distribution.
In all the experiments, in order to confirm the
effectiveness of the method aimed at improving the
diversity and homogeneity of the solution
distribution, we confirmed that the solution searches
had adequately converged by comparing the Pareto
front diagrams of solutions from the 1,000th
generation with those of the conventional method.
4.2.1 Comparison of Solution Distributions
for Population Size 20
For the case of ZDT1 in Fig. 8, the proposed method
causes the total number of non-inferior solutions at
both ends of the Pareto front (where objective
function 1 lies in the ranges 0–0.2 and 0.8–1.0) to
increase from 9 to 12 as shown in Table 3. Similarly,
for the case of ZDT2 in Fig. 9, the proposed method
increases the number of non-inferior solutions at the
ends of the Pareto front (0–0.2 and 0.8–1.0) from 6 to
8, while in other regions it produced solutions that
were distributed more uniformly along the Pareto
front than the conventional method. This improved
diversity is thought to have occurred because the
ability to generate solutions at both ends of the Pareto
front was improved by the proposed method whereby
the solutions at both ends of Rank 2 were used for
genetic manipulation, resulting in greater diversity.
Also, by swapping solutions at both ends of Rank 2
with the solutions in Rank 1 that have the smallest
crowding distance in the archive population, it
appears that we were able to generate solutions in the
range from 0.2–0.8 with a large crowding distance,
resulting in a solution distribution with greater
dispersion.
(a) Conventional method
(b) Proposed method
Figure 8: Comparison of solution distribution diagrams for
ZDT1.
Table 2: Number of non-dominated solutions for ZDT1.
Value of objective
function 1
Conventional
method
Proposed
method
0–0.2 6 7
0.8–1.0 3 5
Total 9 12
(a) Conventional method (b) Proposed method
Figure 9: Comparison of solution distribution diagrams for
ZDT2.
Table 3: Number of non-dominated solutions for ZDT2.
Value of objective
function 1
Conventional
method
Proposed
method
0–0.2 2 3
0.8–1.0 4 5
Total 6 8
In the case of ZDT3 shown in Fig. 10, it was not
possible to clearly confirm the breadth of the solution
with 20 individuals because the Pareto front was
discontinuous. On the other hand, looking at each
group of solution groups, it can be seen that the
solutions are more uniformly dispersed than in the
conventional method. In the same way as in the case
of XDT2, this effect is thought to be caused by
performing genetic operations with Rank 2 solutions
that have a large crowding distance instead of Rank 1
solutions that have a small crowding distance.
(a) Conventional method (b) Proposed method
Figure 10: Comparison of solution distribution diagrams for
ZDT3.
On the other hand, the result is just one example
in which the diversity is obviously improved, and
there was some variation in accuracy among the 10
runs. A common trend observed with ZDT1 and
ZDT2 was that the number of solutions created at
both ends of the distribution did not necessarily
increase significantly, but an improvement in the
Using Dominated Solutions to the Uniformity of Non-dominated Solution Distributions in NSGA-II
217
uniformity of the solution distribution was observed
in many cases. From the above, it was confirmed that
with a population of 20 individuals, the ability to
generate solutions at both ends of the distribution was
improved, leading to an improvement in the overall
diversity of the solution distribution. This is thought
to be because the elimination of Rank 1 solutions
having a small crowding distance instead of Rank 2
solutions at both ends of the Pareto front reduces the
generation of solutions in the range between 0.2 and
0.8, which was densely occupied in the conventional
method, making it more likely that candidates in the
next generation are created at the ends of the solution
distribution.
4.2.2 Comparison of Solution Distributions
for Population Size 100
Next, Figs. 11 through 13 show the results obtained
with a population size of 100. These diagrams show
examples where it was confirmed that the number of
individuals generated at both ends of the distribution
was larger than in the conventional method. From
Tables 4 and 5, it can be seen that the number of
individuals increased slightly at both ends of the
solution distribution. On the other hand, when
observing the 10 experiments one by one, the results
showed that the diversity of solutions did not
necessarily improve significantly. This may have
been caused by the number of individuals. With a
hundred individuals, the population size may have
been so large relative to the size of the search space
that exchanging only two solutions at both ends of
Rank 2 was unable to significantly affect the ability
to search for solutions.
(a) Conventional method (b) Proposed method
Figure 11: Comparison of solution distribution diagrams for
ZDT1.
Table 4: Number of non-dominated solutions for ZDT1.
Value of objective
function 1
Conventional
method
Proposed
method
0–0.2 30 32
0.8–1.0 15 17
Total 45 49
(a) Conventional method (b) Proposed method
Figure 12: Comparison of solution distribution diagrams for
ZDT2.
Table 5: Number of non-dominated solutions for ZDT2.
Value of objective
function 1
Conventional
method
Proposed
method
0–0.2 11 11
0.8–1.0 27 29
Total 38 40
(a) Conventional method (b) Proposed method
Figure 13: Comparison of solution distribution diagrams for
ZDT3.
4.2.3 Comparison of Changes in
Hypervolume
Since the same tendency arose for all the test
functions, Fig. 14 shows the relationship between the
number of generations and the HV value for the case
of ZDT2, which was suitable for evaluating diversity.
(a)
20 individuals (b) 100 individuals
Figure 14: The relationship between the number of
generations and the HV value.
As a result, with 20 individuals, the proposed
method produced a slightly higher HV value for
ZDT2, but with 100 individuals, no significant
difference was observed. Since the ZDT2 test
optimization problem is suited to the evaluation of
diversity, it is thought that the proposed method was
able to work effectively on this problem because it
focuses on improving diversity. However, since it
ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications
218

depends on randomly generated initial individuals,
and since the HV values varied widely over 10
experiments, a more detailed investigation is needed
in the future. Therefore, although the proposed
method is not particularly effective at improving the
HV value, it could be highly effective at improving
the diversity on the Pareto front and improving the
uniformity of the non-inferior distribution, depending
on the characteristics of the problem and the number
of individuals.
4.3 Future Works
As a future work, we evaluated the proposed method
using the ZDT suite this time, but it is also necessary
to evaluate using the knapsack problem and TSP that
challenge the algorithm to find the boundary
solutions. In addition, since initial value dependence
was observed in this experiment, significance testing
such as t-test should be performed. Furthermore, this
time, the experiment was conducted without changing
the reference point values of the previous experiment,
but there is a paper (Li, 2019) that the solution
accuracy greatly depends on the reference point
value. Therefore, an evaluation experiment with
different reference points is also necessary.
There is a paper (Ohki, 2018) using Pareto partial
dominance for the problem when NSGA-II does not
work effectively in the many-objective optimization
problem. Similar to the proposed method, this is a
countermeasure when the search using the dominant
/non-dominated relationship does not work
effectively. This method is considered to be effective
when the number of objectives is 4 or more, but when
applied to a multi-objective problem with 3 or less
objectives, a single-objective search occurs. On the
other hand, our proposed method is also an effective
method for multi-objective optimization problems
with 3 or less objectives. Both can be applied in
combination, and further comparative studies
including the applying method are required in the
future.
5 CONCLUSIONS
In this paper, we proposed a method whereby, in the
NSGA-II evolutionary multi-objective optimization
algorithm, some of the inferior solutions outside Rank
1 that would normally be culled during the search
process are instead preserved and actively used for
genetic operations, which may be an effective way of
actively improving diversity. When preserving these
inferior solutions, we used them to replace solution
candidates in Rank 1 that had a small crowding
distance and were densely located on the Pareto front.
Using the typical ZDT1, ZDT2 and ZDT3 test
functions, we experimentally compared this method
with the original NSGA-II algorithm, but found no
improvement in the final hypervolume value.
However, our method was possible to improve the
diversity of solutions and the uniformity of the non-
inferior solutions at both ends of the Pareto front,
especially when the population size was small.
ACKNOWLEDGEMENTS
This work was supported by JSPS KAKENHI Grant
Numbers JP19K12162.
REFERENCES
Beume, N., Fonseca, C. M., Lopez-Ibanez, M., Paquete, L.,
Vahrenhold, J., 2009. On the complexith of computing
the Hypervolume indicator. In IEEE Transaction on
Evolutionary Computations, Vol. 13, No. 5, pp. 1075-
1082, IEEE.
Carlos, A. Coello C., 2006. Evolutionary multi-objective
optimization: A historical view of the field. In
Computational Intelligence Magazine, Vo. 1, No. 1, pp.
28 – 36, IEEE.
Deb, K., Agrawal, S., Pratap, A., Meyarivan, T., 2002. A
fast and elitist multiobjective genetic algorithm:
NSGA-II. In IEEE Transactions on Evolutionary
Computation, Vol. 6, No. 2, pp182-197, IEEE.
Sato, H., Aguirre, H.E., Tanaka, K., 2007. Local
Dominance Including Control of Dominance Area of
Solutions in MOEAs. In MCDM 2007. Proceedings the
2007 IEEE Symp. on Computational Intelligence in
Multi-Criteria Decision-Making. pp. 310-317, IEEE.
Srinivas, N., Deb, K., 1994. Multiobjective Optimization
Using Non-dominated Sorting in Genetic Algorithms.
In Evolutionary Computation, Vol. 2, No. 3, pp. 221-
248, MIT Press.
Zitzler, E., Laumanns, M., Thiele, L., 2001. SPEA2:
Improving the Performance of the Strength Pareto
Evolutionary Algorithm. In Technical Report 103,
Computer Engineering and Communication Networks
Lab (TIK), Swiss Federal Institute of Technology.
Li, M., Yao, X., 2019. Quality Evaluation of Solution Sets
in Multiobjective Optimisation: A Survey. In ACM
Computing Surveys, Vol. 52, No. 2, pp. 1-43, ACM.
Ohki, M., 2018. Linear Subset Size Scheduling for Many-
objective Optimization using NSGA-II based on Pareto
Partial Dominance. In Proceedings of the 15th
International Conference on Informatics in Control,
Automation and Robotics (ICINCO 2018). Vol.1, pp.
277-283.
Using Dominated Solutions to the Uniformity of Non-dominated Solution Distributions in NSGA-II
219
