
BLOCK AND QUADTREE BASED SIMPLIFICATION IN TILED
BLOCKS TERRAIN ALGORITHMS
Ivo Leitão and Beatriz Carmo
Faculdade de Ciências, Universidade de Lisboa, Campo Grande, Lisboa, Portugal
Keywords: Terrain Rendering Algorithms, Level-of-Detail, Spatial and Temporal Coherence.
Abstract: With the advent of modern graphic processors, rendering a complex terrain in real time was suddenly
possible. However the constant struggle between rendering quality and real time performance is still
demanding more that we can actually get. Terrains are a prime example of that, the sheer amount of
geometry and the constant need to achieve higher standards in image quality are always taking the graphical
processors to their limits. Level of detail techniques, are therefore very important in this area and were used
in multiple algorithms through the years. Tiled blocks are a category of terrain algorithms where the terrain
is partitioned into square patches that are tessellated at different resolutions. This paper describes and
compares two of the most common approaches used in the simplification process: block based
simplification, where the simplification is local to the block, and quadtree based simplification, which uses
the spatial partitioning principle of the quadtree to perform the simplification.
1 INTRODUCTION
Rendering terrain areas is an integral part of many
applications, ranging from the entertainment
industry to architectural visualizations, cartography
applications and military simulations. Unfortunately
it is still a difficult challenge, despite the ever
growing power of the graphical processors available
today. To cope with that, level of detail techniques
appeared as an essential tool in this area especially
for large terrains. Most of them were used in the
course of years in a number of algorithms that were
specially designed for the rendering of large terrains
at interactive frame rates. Two of the most
commonly used, especially by the game industry, are
the Geomipmapping (Boer, 2000) and the Chunked
LOD (Ulrich, 2002) algorithms. They belong to a
class of terrain algorithms commonly described as
Tiled Blocks, following the classification proposed
in (Lossaso, 2004). In these algorithms, the terrain is
partitioned into square patches that are tessellated at
different resolutions. In the Geomipmapping
algorithm the level of detail decreases by the
individual simplification of each block. In the
Chunked LOD algorithm the level of detail
decreases by the substitution of four blocks by one
that represents the same area. Our objective was to
analyze these two approaches, not by the specific
features of each individual algorithm but in more
general terms as two different simplification
techniques shared by other algorithms in the same
category. We called this two approaches block based
and quadtree based simplification and they will be
the focus of this paper.
This paper is organized as follows. In Section 2
we talk briefly about the evolution of terrain
rendering algorithms giving special emphasis to tiled
block approaches. In Section 3 the main concepts
beyond the two types of simplification are
explained. In Section 4 the common points in the
two simplification methods are highlighted and how
we unified them under a unique framework. In
Section 5 the role of the error metric in the
simplification process is described. In Section 6 are
discussed methods to correct cracks between
adjacent blocks with different levels of detail. In
Section 7 geomorphing is described as the method
used to correct the “popping” effect resulting from a
change of detail. In Section 8 the testing
environment and the particular features implemented
for each simplification algorithm are described. In
Section 9 results of the performed tests are presented
and in Section 10 we summarize the conclusions and
point out future work.
205
LeitÃ
ˇ
co I. and Carmo B.
BLOCK AND QUADTREE BASED SIMPLIFICATION IN TILED BLOCKS TERRAIN ALGORITHMS.
DOI: 10.5220/0001797502050210
In Proceedings of the Fourth International Conference on Computer Graphics Theory and Applications (VISIGRAPP 2009), page
ISBN: 978-989-8111-67-8
Copyright
c
2009 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
2 RELATED WORK
Terrain rendering algorithms have a long history,
and a comprehensive overview of this subject is
beyond the scope of this paper. For a more detailed
presentation, we refer the reader to (Pajarola, 2007).
In the following we will briefly trace a temporal line
covering the most important algorithms and trends
with special emphasis on the tiled block techniques.
From a historical perspective the first algorithms
specially designed for the rendering of terrains
appeared in the late seventies, for example (Fowler,
1979). However it was only in the middle nineties,
when consumer hardware was already capable of
representing terrains in real time, that some of the
most important algorithms appeared. Approaches
like (Lindstrom, 96), (Duchaineau, 97) and (Rottger,
98) became very popular. For most of them the main
objective was to reach the perfect triangulation
reducing the number of triangles processed by the
graphic card but increasing the work on the CPU
side. However, with the appearance of powerful
graphical processors, reaching the perfect
triangulation stopped being the main objective. On
the contrary, sending big blocks of geometric data to
the GPU is now the dominating trend. This means
that the focus switched from the triangle to blocks of
geometry which became in this process the new
target of level of detail techniques. To deal with this
new reality new types of algorithms started to appear
mainly tiled block approaches that applied level of
detail techniques to blocks of geometry. Algorithms
like (Boer, 2000), (Ulrich, 2002), (Laurisen, 2005)
and (Vistnes, 2006) are only examples of approaches
that followed this new trend. The most recent
algorithms are taking this trend even further
offloading most of the work to the graphical
processor. They use concentric rings of detail that
work on a focal area using a windowed view of the
terrain. One of the main characteristics of this new
approach is the usage of vertex textures, a new
functionality of shader model 3.0. This functionality
enables the sampling of a texture in the vertex
shader. This is particularly useful for terrain
rendering, since it enables the storage of the
elevation values in a texture which can be used in
the vertex shader to displace the vertices.
Algorithms like (Asirvatham, 2005) (Clasen, 2006)
and (Pangerl, 2008) are good examples of this.
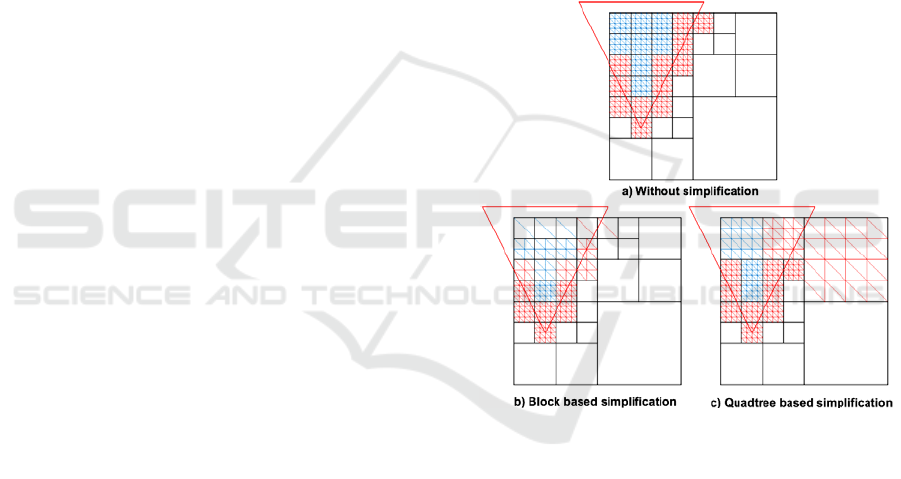
3 SIMPLIFICATION METHODS
To comprehend the differences between block based
simplification and quadtree based simplification we
have to understand precisely what happens in each
one of the methods. For that, we will use a top view
representation of a recursive walk on a quadtree in a
33x33 terrain with a 5x5 block, like the ones
depicted in Figure 1. In this figure the triangle
represents the frustum and the tessellated squares
correspond to the blocks that are contained or
intersected by the frustum. In Figure 1 a) all the
blocks are at maximum resolution (5x5), so it
represents the typical brute force approach to terrain
rendering. Decreasing the resolution, i.e., level of
detail of the blocks, is the purpose of block and
quadtree based simplification. Block size is critical
in these methods because the number of levels
needed to represent the terrain in the quadtree is
based on it.
Figure 1: Simplification methods.
Let us start with block based simplification. This
kind of simplification is depicted in Figure 1 b). In
this method an error metric is used to determine the
most appropriate level of detail for each block, so
the simplification is completely independent from
the one applied to the other blocks. Therefore it is
common to have neighbouring blocks with different
levels of detail. Moreover, the number of vertices
changes according to the detail level but the size of
the block is constant, so the number of draw calls
issued in this method only depends on the number of
blocks that intersect or are contained in the frustum.
With quadtree based simplification like the one
depicted in Figure 1 c), the size of the block can
change but the number of vertices in each block is
constant. This kind of simplification uses the spatial
partitioning principle of the quadtree to determine
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
206

the most appropriate block size. More precisely an
error metric is used on the recursive walk made on
the quadtree to decide the most appropriate block
size for each region of the terrain. Higher levels of
the quadtree represent larger areas of the terrain with
lower detail. Lower levels of the quadtree represent
smaller areas of the terrain with greater detail. This
works recursively from the root node of the quadtree
to the leaf nodes where the underlying resolution of
the terrain is matched. In this method the number of
draw calls depends not only on the point of view but
also on the error metric. Also, a block can have
neighbours with different sizes, making any possible
correlation between blocks difficult to achieve.
4 UNIFYING THE APPROACHES
Making a comparison between these two approaches
will be surely flawed if they are seen as completely
different. The common point here is the underlying
spatial partitioning structure, the quadtree. With that
in mind we can differentiate the two methods by
assuming that each one represents a different way of
making the recursive walk on the quadtree. With a
block based simplification scheme the quadtree is
used only to identify the visible blocks, i.e. blocks
that are intersected or are contained in the frustum.
No level of detail is calculated at this stage and all
these blocks are at the same level in the quadtree as
they have the same block size. Therefore one
possible optimization is to stop the recursion sooner,
when we reach a node that is completely contained
in the frustum even if the resolution of that node
does not match the desired block size. For example,
if the first quadrant of the first level of the quadtree
is completely contained in the frustum, we can stop
the recursion for that branch adding all the blocks of
the desired block size that are contained in this
larger block. Finally for each one of these blocks we
have to choose the most appropriate level of detail
basing our decision on the error metric. With
quadtree based simplification the main difference
lies on the recursion which can stop sooner because
the level of detail evaluation is done for each node
of the quadtree so it is possible to choose larger
blocks and render them. These larger blocks have
the same number of vertices but the space between
those vertices is greater.
To unify this approaches even further we take
advantage of a very useful property in a regular grid
triangulation: every block can be described by a
scale and a translation factor. To make this property
useful we have to separate the elevation values from
the geometric description of the block. This is
achieved with two vertex streams. A vertex stream is
essentially an array of vertex component data. For
instance it is possible to assemble vertices from
several vertex streams, where each stream consists
of a component of the vertex (e.g., one stream
contains position info, another contains colour info,
another texture coordinate info, etc.). In our
approach the first stream contains the position of the
vertices and the second stream contains the elevation
values. Since we use canonical values for the
position of the vertices this vertex data is valid for
all the blocks of the terrain. Later when rendering,
we transform the canonical values in the vertex
shader to obtain the correct position of the block.
For that we only need a couple of uniform shader
parameters, in this case, the scale and the translation
associated with each block.
The main advantage of a multi-stream approach
is that it enables us to use vertex textures in
machines that support shader model 3.0. In this case,
the memory requirements are reduced since we only
need one stream with the geometric description of
the block because the elevation data is stored on a
texture. Without vertex textures we need to send the
elevation values in a second stream.
To connect the vertices in a block we need a list
of indices, however this list is different in each
method. With quadtree based simplification we only
need to describe a block since in this method the
geometrical structure of the block does not change,
only the area that it occupies. With block based
simplification we need to represent all the possible
levels of detail of a block. For example if we have a
5x5 block, like the one used in the previous figures,
we need to represent a 5x5, a 3x3 and 2x2 block.
This is done with different sequences of indices each
one representing one of the aforementioned levels of
detail.
5 ERROR METRIC
The error metric has a very important role to fulfil in
tiled block algorithms as it is used to decide when
the transition to lower/higher detail levels happens.
With block based simplification it is used to control
the level of detail of the block, i.e., when a
higher/lower detailed version of the block should be
used to represent the associated region on the terrain.
With quadtree based simplification it is used to
decide the number of blocks that should represent a
region of the terrain, more precisely when a block
can be substituted by its four more detailed children
BLOCK AND QUADTREE BASED SIMPLIFICATION IN TILED BLOCKS TERRAIN ALGORITHMS
207
or the other way around, to decide when four blocks
can be substituted by its less detailed parent.
The error metric used in the two algorithms is the
one presented in the Geomipmapping algorithm
(Boer, 2000), which uses block based simplification.
This error metric can be easily adapted, as described
in (Laurisen, 2005), to a quadtree based
simplification. It involves the calculation of a
constant C in a pre-processing stage and of a
minimum distance D, for each level of detail n.
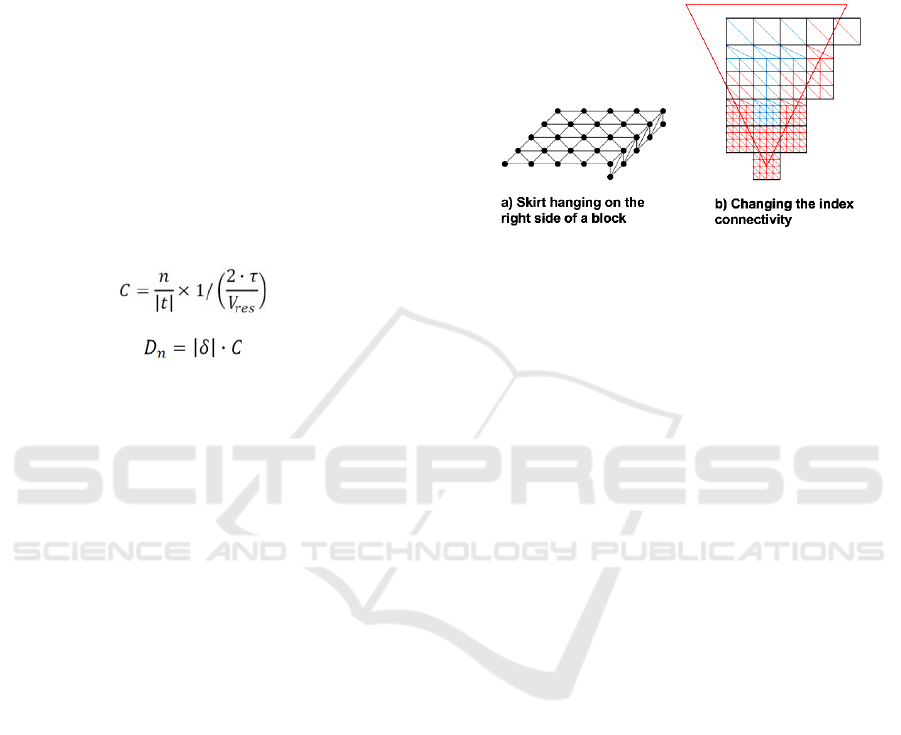
The constant C is calculated with Equation 1,
where n is the near clipping plane, t the top
coordinate of the near clipping plane, τ the error
threshold in pixels and Vres the vertical resolution in
pixels
The D for each level of detail n is calculated
with Equation 2, where δ is the geometric error and
C the constant calculated with Equation 1.
(1)
(2)
6 SPATIAL COHERENCE
The appearance of cracks between neighbouring
blocks with different levels of detail is a common
problem in tiled block approaches like the ones
described in this paper. There are several ways to
correct this problem but most of them are far from
ideal as they have a very noticeable impact in
performance. The fastest methods are the ones that
do not imply changes to the list of vertices or to the
list of indices committed to the graphical processor.
Adding vertical skirts around each block is a
solution that meets this objective. This method was
first introduced in (Ulrich, 2002) and is represented
in Figure 2 a). However, we should select carefully
the skirt size since it can have big impact in the fill
rate. It should be big enough to cover any possible
cracks that can appear between the tile and the
neighbouring tiles but not greater than that.
Note that, for optimal performance the skirts
have to be drawn in the same call as the block so the
vertices and the indices should be arranged to make
that possible. This technique can be used with block
or quadtree based simplification. However this
method does not correct the geometry, in fact the
difference of height between adjacent tiles is only
hidden by the skirts. Another technique that can be
used to correct the cracks is to change the
connectivity (or indexing) of the vertices at the edge
of the block. This was originally suggested in (Boer,
2000) and is exemplified in Figure 2 b) for block
based simplification where the tile with the higher
level of detail adapts its borders to the level of detail
of its neighbour(s). This technique implies changes
to the list of indices at runtime and therefore it is not
completely static, quite the contrary of skirts.
Figure 2: Crack correction methods.
Unfortunately it cannot be used with quadtree
based simplification, since adjacent blocks can
change in size. This means that a block can have
triangles bigger than its neighbours. For example, it
can happen that a triangle spans two or more
neighbouring blocks. In these cases any change in
the index connectivity of the neighbours will not
correct the problem.
7 TEMPORAL COHERENCE
Another important problem with tiled blocks and
with level of detail algorithms in general is the so
called “popping” effect. This is the result of a
sudden change of detail (to more or less detail)
which can originate a very noticeable effect. This is
caused by the appearing or disappearing of vertices
which cause a sudden “pop” in the geometry that is
very unnatural and contributes negatively to the
level of realism that we are trying to achieve. The
most common way of handling this problem is with
geomorphing (Luebke, 2003). The objective is to
slowly morph the vertices from one level of detail to
another. This can either be done over time or based
on the error. The latter is the best approach since in
this way the morphing only occurs when the
viewpoint is moving which helps hide the swirling
artefacts that it can cause. Concerning the
simplification methods discussed in this paper there
is no noticeable differences between the two
approaches since what we really need to know when
moving between levels of detail is which vertices
disappear and the error that results from that. This is
what is normally needed to perform the
geomorphing. Therefore all we need to do is to store
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
208

that information in the list of elevation values since
it changes with each elevation value. This raises a
problem when we use vertex textures to displace the
vertices in the vertex shader since in that situation
we do not have a list elevation values, but only one
texture. The solution is to use another texture to
store for each vertex the level where it disappears
and the resulting error.
The morphing itself is executed on the vertex
shader. Since we receive all the necessary data this
is normally very fast and therefore it should be used
whenever possible as it can help increase the realism
significantly.
8 TESTING FRAMEWORK
We have developed a framework in XNA which
unifies under the same architecture the most relevant
characteristics of tiled blocks algorithms. With this
framework we have implemented the two
simplification methods and a brute force approach
where we did not make any simplification. The
results of brute force algorithm are used as baseline
performance values. We have also implemented
frustum culling which uses the quadtree to test each
block against the frustum as was already mentioned
in Section 4. To reach meaningful results it was
equally important to use the same error metric in the
simplification methods. Geomipmapping (Boer,
2000) error metric was adopted as explained in
section 5. To correct the cracks we have used the
skirt and the index update methods described in
Section 6 and to correct the “popping” effect we
have implemented geomorphing using the
approaches described in (Boer, 2000) and (Laurisen,
2005) for each one of the simplification methods.
Concerning the lightning we used per-pixel
lightning also known as normal mapping (Kilgard,
2000). Finally for the texturing of the terrain we
have used one colour texture.
9 RESULTS
The tests were performed on three computers: a
laptop with a Mobile Intel 945 GM graphical card,
which we called N1, a laptop with a ATI Mobility
Radeon 9700, which we called N2, and a desktop
with a NVIDIA GeForce 7950 GX2 graphical card,
which we called D1. These setups represent two low
end systems with a graphical card that support
shader model 2.0 and a high-end system with a
graphical card that supports shader model 3.0. Two
procedurally generated terrains were used in the
tests: a 1025x1025 terrain, called Terrace, and a
2049x2049 terrain, called Highland.
To gather the performance results we have pre-
recorded a 60 seconds walk on each terrain at
relatively low altitude.
The results obtained using two streams, vertices
and elevation values, are summarized in Table 1
where it is possible to compare the average frames
per second obtained in each terrain. For each
machine we have measured the performance of the
brute force approach and of the two simplification
methods discussed in this paper. We have
considered three different block sizes, 17x17, 33x33
and 65x65 and two types of crack correction
methods: index update and skirts. We have used a
maximum error of 8 pixels.
The quadtree simplification method in
conjunction with skirts was the fastest approach in
two of the three machines considered. This was
expected as the number of draw calls is much lower
in this method. The only exception was the N2
machine where block based simplification was
faster. On the N1 machine, the slowest, it makes in
fact the difference between a working real time
representation of the terrain with a frame rate above
the 60 frames per second and a slow representation
almost unusable and is therefore an obvious choice.
The fastest block size was 17x17 with the exception
of machine N2 where the fastest block size was
33x33. However, on that machine the fastest
simplification method was also different and the two
simplification methods analyzed use different ways
of reducing the detail.
Concerning the crack correction methods used in
block based simplification, in almost every situation
the index update method was slower. In fact it had a
tremendous impact in the performance mainly in
machines N2 e D1. As we have already mentioned
in Section 7, index update implies changes in the list
of indices at runtime and this results confirm that it
can cause a significant frame rate drop.
We have also tested the performance with vertex
textures this time only on the D1 machine since it is
the only that supports shader model 3.0. The results
are summarized in Table 2.
If we compare the results in Table 2 with the
results obtained for the same machine in Table 1 we
can see that using vertex textures is slower. This was
expected since this behaviour was already observed
by other authors, for example it is mentioned in
(Asirvatham, 2005), (Clasen, 2006) and on (Pangerl,
2008). However with vertex textures the fastest
method was block based simplification which shows
that sampling a vertex texture with quadtree based
simplification is somewhat slower than with block
based simplification.
BLOCK AND QUADTREE BASED SIMPLIFICATION IN TILED BLOCKS TERRAIN ALGORITHMS
209

Table 1: Average frames per second.
Brute
Force
Block
(Index Update)
Block
(Skirts)
Quadtree
(Skirts)
Terrace
17x17
52 52 49 126
N1 33x33
43 55 55 99
65x65
26 59 65 45
17x17
107 86 223 211
N2 33x33
102 146
229 180
65x65
92 143 176 139
17x17
606 190 532 1336
D1 33x33
567 328 1302 1051
65x65
514 357 1070 791
Highland
17x17
14 14 13 75
N1 33x33
13 17 17 51
65x65
7 22 25 24
17x17
38 23 74 159
N2 33x33
37 51
174 129
65x65
33 72 131 95
17x17
149 44 121 919
D1 33x33
188 101 498 690
65x65
177 127 785 511
Table 2: Average frames per second with vertex textures.
Brute
Force
Block
(Index Update)
Block
(Skirts)
Quadtree
(Skirts)
Terrace
17x17
384 217 602 742
D1 33x33
256 347
834 329
65x65
216 348 436 252
Highland
17x17
105 52 131 464
D1 33x33
75 112
480 217
65x65
66 125 356 136
10 CONCLUSIONS
We analyzed two of the most common simplification
methods used in tiled block approaches to terrain
rendering. We have discussed algorithms and
techniques to keep temporal and spatial coherence,
respectively, geomorphing and skirts or index
update. We have come to the conclusion that
quadtree based approaches are the best option in
most of the situations, mainly when the terrain is
very large and/or the machine is slow. In these cases
the reduction of the draw calls has a very noticeable
impact in terms of performance.
We have also concluded that skirts are the best
approach to handle the cracks. The other method
implies changes to the list of indices at runtime and
affected performance significantly.
In the future we plan to analyze the impact of
occlusion culling techniques on the performance of
each simplification method and also to pursue new
approaches to the correction of cracks mainly the
generation of all the possible combinations between
a level of detail of a tile and its neighbour’s level of
detail in block based simplification. We are also
planning support out-of-core data to cope with
terrains with sizes beyond the available memory.
ACKNOWLEDGEMENTS
This work was partially supported by LabMAg
through FCT Multiannual Funding Programme.
REFERENCES
Asirvatham A., Hoppe H., 2005. GPU Gems 2. Terrain
Rendering using GPU-Based Geometry Clipmaps.
Addison-Wesley pp 27-45.
Boer, W., 2000. Fast Terrain Rendering Using
Geometrical MipMapping. Available online at
www.flipcode.com/archives/article_geomipmaps.pdf.
Clasen, M., Hege, H.C., 2006. Terrain Rendering using
Spherical Clipmaps. In EuroVis 2006, pp. 91-98.
Duchaineau, M., Wolinsky, M., Sigeti, D. E., Miller, M.
C., Aldrich, C., Mineev-Weinstein, M. B., 1997.
ROAMing terrain: Real-time optimally adapting
meshes. In IEEE Visualization ’97, pp 81-88.
Fowler, Robert J., Little, James J., 1979. Automatic
Extraction of Irregular Network Digital Terrain
Models. In Proceedings SIGGRAPH’79, pp 199-207.
Lossaso, F., Hoppe H., 2004. Geometry clipmaps: Terrain
Rendering Using Nested Regular Grids. In ACM
Transactions on Graphics (TOG), v.23, n.3.
Lindstrom, P., Koller, D., Ribarsky, W., Hodges, L. F.,
Faust, N., Turner, A., 1996. Real-Time, Continuous
Level of Detail Rendering of Height Fields. In
SIGGRAPH ’96, pp 109-118. ACM, New York, NY.
Laurisen, T., Nielsen, S. L., 2005. Rendering Very Large,
Very Detailed Terrains. Available online at http://
www.terrain.dk/terrain.pdf.
Luebke, D., Reddy M., Cohen D., Varshney, A.,
Watson,B., Huebner R., 2003. Level of Detail for 3D
Graphics. Morgan Kaufmann Publishers.
Kilgard, M., 2000. A Practical and Robust Bump-mapping
Technique for Today’s GPUs. NVIDIA Corporation.
Pangerl D., 2008. ShaderX6 - Advanced Rendering
Techniques. Quantized Ring Clipping, pp 133-140.
Charles River Media.
Pajarola, R., Gobbetti, E., 2007. Survey on Semi-Regular
Multiresolution Models for Interactive Terrain
Rendering. In Vis. Comput. 23, 8, pp 583-605.
Rottger, S, Heidrich, W., Slussalek, P., Siedel, H., 1998.
Real-Time Generation of Continuous Levels of Detail
for Height Fields. Proc. WSCG’98, pp 315-322.
Ulrich, T., 2002. Rendering Massive Terrains Using
Chunked Level of Detail Control. In SIGGRAPH ’02
Course Notes.
Vistnes, H., 2006. Game Programming Gems 6. GPU Ter-
rain Rendering, pp. 461–471.Charles River Media Inc.
GRAPP 2009 - International Conference on Computer Graphics Theory and Applications
210
