CHOSEN-IV STATISTICAL ATTACKS ON eSTREAM CIPHERS

Markku-Juhani O Saarinen

Royal Holloway, University of London

Egham, Surrey TW20 0EX, UK

Keywords:

Stream Ciphers, eSTREAM, Algebraic Normal Form, M

obius test, d-monomial test.

Abstract:

d-Monomial tests are statistical randomness tests based on Algebraic Normal Form representation of a Boolean

function, and were ﬁrst introduced by Filiol in 2002. We show that there are strong indications that the Gate

Complexity of a Boolean function is related to a bias detectable in a d-Monomial test. We then discuss how

to effectively apply d-Monomial tests in chosen-IV attacks against stream ciphers. Finally we present results

of tests performed on eSTREAM proposals, and show that six of these new ciphers can be broken using the

d-Monomial test in a chosen-IV attack. Many ciphers even fail a trivial (ANF) bit-ﬂipping test.

1 INTRODUCTION

Statistical testing has traditionally been a part of eval-

uation of stream ciphers. However, most cryptogra-

phers agree that generic tests such as the NIST 800-22

suite are appropriate mainly for catching implementa-

tion errors rather than determining the cryptographic

strength of an algorithm (Murphy, 2000; Rukhin et al,

2001).

Usually these tests have been performed in a pas-

sive setting; a sequence of bits is generated under a

(random) key, and these bits are then subjected to a

generic statistical test. What is ignored in this ap-

proach is that stream ciphers equipped with an Initial-

ization Vector (IV) should also be able to withstand

chosen-IV attacks, where a sequence of data is gener-

ated by varying the IV value rather than the “counter”

value (see Figure 1).

Stream ciphers are optimized for security, but also

for speed and cost. Cost in many applications equates

to the number of logical gates in a hardware imple-

mentation of the cipher, and hence designers usually

attempt to minimize their gate complexity.

Most stream ciphers can be speciﬁed as a relatively

simple iterated function. As a result of this, it has

been observed that some keystream bits can be ex-

pressed as simple Boolean functions of the key and IV

bits. In a chosen-IV attack, the key bits remain con-

stant and the stream cipher can be viewed as a “black

box” Boolean function of the IV alone.

In a chosen-IV distinguishing attack, an attacker

would wish to be able to determine whether or not

a keystream bit (say, the ﬁrst one after IV setup) is a

simple Boolean function of some IV bits simply by

making queries to this black box.

How would one automatically distinguish such a

Boolean function of n bits from a random one? One

solution is to examine its Algebraic Normal Form

(ANF) representation for anomalies such as redun-

dancy or bias. A test that utilizes this approach was

ﬁrst proposed by Eric Filiol in 2002 (Filiol, 2002). In

this paper we will give further theoretical and exper-

imental evidence of the applicability of ANF-based

tests on stream ciphers.

The structure of this paper is as follows. In Section

2 we recall the Algebraic Normal Form and its basic

properties. Section 3 contains an exposition of a vari-

ant of Filiol’s d-monomial statistical test. Section 4

gives new, clear evidence of the relationship between

Boolean gate complexity and the d-monomial test.

Section 5 discusses a simple statistical attack based

on ﬂipping input bits that was found to be surpris-

ingly effective against eSTREAM ciphers (Estream,

2006). Section 6 contains new results on statistical

tests on the 34 eSTREAM cipher proposals, followed

by conclusions in Section 7.

260

O Saarinen M. (2006).

CHOSEN-IV STATISTICAL ATTACKS ON eSTREAM CIPHERS.

In Proceedings of the International Conference on Security and Cryptography, pages 260-266

DOI: 10.5220/0002098302600266

 SciTePress

black

box

"Counter"

Public IV

Secret Key

Keystream

Figure 1: A stream cipher can be seen as a black box

Boolean function that takes in a secret key, a public IV, and

a public “counter” to produce a single bit of keystream.

2 PRELIMINARIES

Let F

be the vector space deﬁned by n-vectors x =

, x

, . . . , x

), where x

∈ F

, i.e. each of the n

elements has either value 0 or 1 and computations are

deﬁned modulo 2. A Boolean function f of n vari-

ables is simply a mapping f : F

7→ F

. There are

exactly 2

distinct Boolean functions of n variables,

each uniquely deﬁned by its truth table.

There are many alternative representations for

Boolean functions, such as Conjunctive and Disjunc-

tive Normal Forms (CNF and DNF), which are widely

used in automated theorem proving and other ﬁelds of

theoretical computer science. We will focus on Alge-

braic Normal Form (ANF, also known as Ring Sum

Expansion, or RSE (Wegener, 1987)).

Deﬁnition. A function

f : F

7→ F

satisfying

f(x) =

a∈F

f(a)

i=1

is an Algebraic Normal Form representation of a

Boolean function f : F

7→ F

Using transformed function

f, a multivariate poly-

nomial representation of f can be obtained as can be

seen from the following example (or directly from the

deﬁnition).

Example. Consider the Boolean function f :

7→ F

deﬁned by the following table:

f(0, 0, 0) = 1, f(1, 0, 0) = 0,

f(0, 1, 0) = 1, f(1, 1, 0) = 0,

f(0, 0, 1) = 1, f(1, 0, 1) = 1,

f(0, 1, 1) = 0, f(1, 1, 1) = 1.

As indicated by Deﬁnition 2, we wish to ﬁnd a

f that

This transform is sometimes confusingly called the

obius transform (Filiol, 2002), hence the name, “M

obius

test” in Filiol’s original paper.

for all x satisﬁes

f(x

, x

) =

f(0, 0, 0) +

f(1, 0, 0)x

f(0, 1, 0)x

f(1, 1, 0)x

f(0, 0, 1)x

f(1, 0, 1)x

f(0, 1, 1)x

f(1, 1, 1)x

this corresponds to solving the following system of

linear equations

in F

1 0 0 0 0 0 0 0

1 1 0 0 0 0 0 0

1 0 1 0 0 0 0 0

1 1 1 1 0 0 0 0

1 0 0 0 1 0 0 0

1 1 0 0 1 1 0 0

1 0 1 0 1 0 1 0

1 1 1 1 1 1 1 1

f(0, 0, 0)

f(1, 0, 0)

f(0, 1, 0)

f(1, 1, 0)

f(0, 0, 1)

f(1, 0, 1)

f(0, 1, 1)

f(1, 1, 1)

f(0, 0, 0) = 1

f(1, 0, 0) = 0

f(0, 1, 0) = 1

f(1, 1, 0) = 0

f(0, 0, 1) = 1

f(1, 0, 1) = 1

f(0, 1, 1) = 0

f(1, 1, 1) = 1

The solution to this matrix equation is obtained eas-

ily with Gaussian elimination:

f(0, 0, 0) = 1,

f(1, 0, 0) = 1,

f(0, 1, 0) = 0,

f(1, 1, 0) = 0,

f(0, 0, 1) = 0,

f(1, 0, 1) = 1,

f(0, 1, 1) = 1,

f(1, 1, 1) = 1.

The ones in

f directly give the ﬁve monomials in

the polynomial expression for f:

f(x

, x

) = 1 + x

+ x

2.1 Properties of the Algebraic

Normal Form

We brieﬂy summarize some of the most important

properties and concepts (facts) of ANF that are rel-

evant to the present discussion:

F.1 A unique

f exists for all Boolean functions f.

F.2 The ANF transform is its own inverse, an involu-

tion; iff g =

f, then ˆg = f.

F.3 We deﬁne a partial order for vectors x as follows:

x ≤ y iff x

≤ y

for all i. Using the partial order,

Deﬁnition 2 can be written as

f(x) =

a≤x

f(a).

CHOSEN-IV STATISTICAL ATTACKS ON eSTREAM CIPHERS

261

F.4 The Hamming distance d(x, y) between x and y is

the number of positions where x

6= y

F.5 A norm, called the Hamming weight, wt(x) =

d(0, x), is equivalent to number of positions in x

where x

= 1.

F.6 The algebraic degree deg(f) is the maximum

Hamming weight x that satisﬁes

f(x) = 1; this

is equivalent to the length of the longest monomial

(most variables) in the polynomial representation

of f .

F.7 Functions of degree one are afﬁne functions. If the

constant term

f(0, 0, . . . , 0) = 0, an afﬁne function

is simply a sum of some of its input bits and called

a linear function.

F.8 A d-Truncated Algebraic Normal Form of Boolean

function f, denoted

(x), is equal to

f(x) when

wt(x) ≤ d, and zero otherwise. In essence, mono-

mials of degree greater than d have been removed

from the corresponding polynomial of the trun-

cated ANF.

F.9 Since

f(x) is the sum of f at all positions with

smaller or equal partial order (and hence degree)

than x (F.3), it can be seen that if we have tabu-

lated f(y ) at all positions y with wt(y) ≤ d, the

d-truncated ANF can be completely determined.

2.2 Computing the ANF

Networks and algorithms for computing the complete

ANF do not require more than n2

n−1

additions in F

Let z : F

7→ Z be the standard mapping from bi-

nary vectors to integers; z(x) =

i=1

i−1

. Let v

be a binary-valued vector of length 2

that contains

the truth table of f; v

z(x)+1

= f(x) for all x. Algo-

rithm 1 gives a fast method for computing

Algorithm 1 Compute the Algebraic Normal Form in

vector v of length 2

using two auxiliary vectors t and

u of length 2

n−1

for j = 1, 2, 3, . . . , n do

for i = 1, 2, . . . , 2

n−1

← v

2i−1

← v

2i−1

⊕ v

end for

v ← t || u

end for

The complexity of Algorithm 1 is clearly

O(n lg n). Variants of this algorithm can be

implemented very efﬁciently using shifts and

bit-manipulation operations.

3 THE D-MONOMIAL TESTS

In (Filiol, 2002) Filiol introduced “M

obius tests”,

which examine whether or not an ANF expression

of a Boolean function has the expected number of d-

degree monomials. With d = 0 the test is called the

Afﬁne test and for d > 0 a d-Monomial test.

Please note that the following exposition of the test

/ distinguisher is signiﬁcantly simpler and less formal

than that originally proposed by Filiol. Details have

been modiﬁed for the purposes of this paper. The

reader is encouraged to use (Filiol, 2002) as a refer-

ence for Filiol’s version of the test.

In practical terms the d-Monomial test involves

counting the number of ones

f(x) = 1 of an ANF

transformed function f at positions x with Hamming

weight d. A d-truncated ANF is is sufﬁcient for this

purpose. A χ

statistical test is then applied to this

count to see if the count is exceptionally high or low.

Theorem. For a randomly chosen n-bit Boolean

function f , Pr[

f(x) = 1] = 1/2 for all x.

Proof. Trivial. Since the ANF transformation is

bijective on the truth table of f,

f will be random if f

is.

Consider an n - bit Boolean function f . Our

null hypothesis is that the expected bitcount

wt(x)=d

f(x) is





and the bitcount is binomially

distributed. The alternative hypothesis is that there is

a bias in this sum, up or down.

We can use Pearson’s classic χ

test in this case.

Suppose that we sample

f at N distinct points (in this

case with wt(x) = d) and in M of those

f(x) = 1.

Then we set

(2M − N)

Since ”0” and ”1” cases in bitcount are mutually

exclusive, there is one degree of freedom in the test.

Using the cumulative degree-one distribution function

of χ

, we can determine a conﬁdence level for f be-

ing distinguishable from random in our test. We call

this the P value and its intuitive interpretation is the

“probability that the null hypothesis is true”. For ex-

ample, if P is 0.01, there’s still a 1% probability that

the null hypothesis is true (and the function is, in this

sense, “random”).

Some “upper critical” values for χ

and the corre-

sponding P values are given in the following table:

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

262

6.635 0.01

10.83 0.001

18.70 2

−16

40.17 2

−32

24.02 2

−40

83.82 2

−64

105.8 2

−80

This type of test is dependent upon the sample size;

even a very slightly biased function will yield a high

value by the test if the sample size is allowed to be

arbitrarily large. The sample sizes are bound by com-

putational restrictions, however. A distinguishing at-

tack is not relevant unless its total expected computa-

tional complexity is smaller than the claimed security

level of the cipher (typically equivalent to 2

k−1

key

trials, where k is the size of the secret key).

4 GATE COMPLEXITY AND THE

D-MONOMIAL TEST

In this section we will give a formal deﬁnition for gate

complexity and investigate its relationship with the d-

Monomial test. Gate complexity is essentially equiv-

alent to circuit complexity with realistic limitations

(Clote, 2002; Wegener, 1987).

Deﬁnition. Gate complexity of a Boolean function

f(x

, x

, . . . , x

) is the minimum number of gates

required to implement it in an acyclic circuit network.

A gate is a Boolean function with two inputs. The

constant functions 0 and 1, together with trivial func-

tions x

, x

, . . . have gate complexity 0.

Note that all 2

= 16 two-bit functions count as a

single gate, not just the standard ones (∨, ∧, ¬, ⊕).

We have determined the gate complexity of all

= 65536 four-bit Boolean functions. This was

done by performing an exhaustive search over all cir-

cuits with one gate, two gates, etc, until circuits for all

functions had been found. The task was computation-

ally nontrivial, even though we optimized the code to

take various symmetries and isometries into account.

The maximum gate complexity turned out to be 7 (see

Figure 2).

Table 1 gives the distribution of functions by gate

complexity. In it, G

is the number of functions of

gate complexity i. These sum to

= 65536.

Here g

i,d

is the number of monomials of degree d and

gate complexity i. These sum to

i,d

= G

. The

maximum possible value for g

i,d

is G





. The ex-

pected number in a d-monomial test is half of this

value. The table contains the “bias” fraction q

i,d

/(G





Note how in Table 1 the d-Monomial “bias” q

i,d

tends to be strongly increasing as the gate complex-

ity i grows (apart for anomaly at q

6,4

). This is clear

evidence of a correlation between the complexity of a

Boolean circuit and the d-monomial test. It is plausi-

ble to expect that a similar phenomenon is exhibited

by Boolean functions with 5, 6, . . . inputs. However,

the exact degree of this bias is currently an open prob-

lem for n > 4. We can expect simple functions to be

distinguishable in a d-monomial test even when n is

large.

It is interesting to note that it is even possible to test

the opposite; to distinguish a complex function from a

randomly chosen one, as the following example illus-

trates.

Example. With the 2720 functions of gate com-

plexity 7, all d-Monomial counts appear to be biased

upwards; q

7,d

≥ 0.5. We will use a d-Monomial test

to create a distinguisher based on this fact, particu-

larly that q

7,1

= 0.606.

Consider the following game. There is a list L con-

taining binary vectors of length 5. Entries in L are

may have been generated with one of the following

two methods:

1. Choose a random 4-bit Boolean function of gate

complexity 7 for each entry, and add the following

vector to the list

(f(0, 0, 0, 0), f(1, 0, 0, 0), f(0, 1, 0, 0),

f(0, 0, 1, 0), f(0, 0, 0, 1)).

2. Choose a completely random Boolean function

(one of the 65536 possibilities) and create a vector

in similar fashion.

We pose the following question: How long does L

need to be for us to see which type of list it is ?

We ﬁrst note that the vectors contain sufﬁcient in-

formation for computation of 1-Monomial test (e.g.

f(1, 0, 0, 0) = f(0, 0, 0, 0) + f (1, 0, 0, 0)). Each 1-

Monomial test is simply the sum of 4 bits in the ANF

result. The expected sum after n list entries is 2n for a

random function and based on our exhaustive search,

7,1

n/G

= 6592/2720n ≈ 2.424n for a gate com-

plexity 7 function. Our distinguisher will simply re-

turn “a” if the sum is greater than 2n and “b” other-

wise.

In the second, fully random case, the distinguisher

has no advantage as the bits in the vector are random

too; “a” and “b” will both be returned with probability

1/2 regadless of the length of L.

In case 1, after n = 34 steps, the sum can be ex-

pected to reach 2.424∗34 = 82.4. ”a” will be returned

by the distinguisher with probability 99%. Hence we

can distinguish the list of (partially computed and ran-

domly chosen) “complex” functions with signiﬁcant

certainty with a list of only 34 entries! Note that the

CHOSEN-IV STATISTICAL ATTACKS ON eSTREAM CIPHERS

263

probability here was computed exactly using binomial

sums, rather than using the χ

test.

5 THE (ANF) BIT-FLIP TEST

The bit-ﬂip test is a simple statistical test that mea-

sures the effect of ﬂipping one of the input bits on a

Boolean function. The test can be performed either

on the function f itself or its ANF counterpart

The same “bit-counting” χ

test with one degree of

freedom can be applied as in d-Monomial test (Sec-

tion 3).

Given a vector with b with wt(b) = 1, we sample

f(x) (or

f(x)) at N distinct points with x

= 0 and

count the number of occurrences M where f(x) =

f(x + b) (or, respectively,

f(x) =

f(x + b)). The

statistic is again

(2M − N)

and the conﬁdence level P is computed in the same

fashion as with d-monomial test.

This simple test is useful for measuring the basic

mixing properties of the function and was therefore

employed in our tests of eSTREAM proposals as dis-

cussed in the following section.

6 CHOSEN-IV TESTS ON

ESTREAM PROPOSALS

As there were as many as 34 proposals for eS-

TREAM (Estream, 2006), some with poor documen-

tation, we decided to make certain assumptions about

their structure in order to facilitate “automatic” d-

Monomial and bit-ﬂipping testing.

1. We wish to ﬁnd a subset of input bits that is likely

to receive less mixing during the IV setup process

than other bits. This is likely to be either at the

beginning or the end of the IV bit-vector.

2. After the bits for a d-Monomial test have been cho-

sen, the remaining constant IV bits also greatly af-

fect the probability that the keystream will exhibit

bias. We chose to run the tests with these bits set as

0 and also when they are set to 1.

3. Rather than running the test on some low-degree

limit d (In (Filiol, 2002) d ≤ 3 and d ≤ 5 are

mentioned), we limit the number of bits n to some

manageable number and compute all d-Monomial

tests on those bits.

There are four d-Monomial tests in total; {bits in

beginning, bits in the end} × {rest of bits set to 0, rest

of bits set to 1}. In practice the black box function (IV

setup) was run with increasing values of n until a time

or memory limit was exceeded. An ANF was then

computed and monomials of various degrees counted.

The same data was also subjected to bit-ﬂipping tests

as described in Section 5.

The testing code was integrated into the “eS-

TREAM speed testing framework”, which allowed

the test to be easily run on most eSTREAM ciphers.

The test code simply utilizes the eSTREAM API and

treats each cipher as a black box function.

There appears to be bugs in some cipher imple-

mentations, that resulted in exceedingly high biases.

Those cases are ignored in the discussion below. We

only mention ciphers where deﬁnitive evidence of sta-

tistical anomaly was detected (positive results are not

reported). All tests were run at least 10 times with

randomized keys. We only report anomalies that re-

occurred in a consistent pattern in distinct tests. Note

that when the same tests were run on reference ciphers

such as AES-CTR, no anomalies were found.

All speciﬁcations of the ciphers are available from

the eSTREAM web site (Estream, 2006). The follow-

ing list of results is not exhaustive, but just relates to

the current status of the tests.

6.1 MAG, Frogbit and F-FCSR

MAG is a stream cipher designed by Rade Vuckovac

that uses a 128-bit key and a 32-bit IV. Frogbit is a

“cipher, data integrity algorithm” designed by Thierry

Moreau with 128-bit key and IV values. F-FCSR is a

family of stream ciphers designed by Thierry Berger,

Franc¸ois Arnault and C

edric Lauradoux.

These ciphers exhibited extreme biases. In some

cases ﬂipping a particular bit in IV did not affect the

ﬁrst keystream bits at all. The designers of these ci-

phers appear to have failed to consider the implica-

tions of chosen-IV attacks.

6.2 DECIM

Decim is a stream cipher with a 80-bit key and a 64-bit

IV designed by Come Berbain et al. Decim is highly

vulnerable to d-Monomial distinguishers. Biases that

occur with P < 2

−96

(our implementation precision

limit) were consistently found. Decim also appears

to be susceptible to a bit-ﬂipping attack, although to

a lesser degree. In a typical run of 2

IV setups, a

bit-ﬂipping bias with P < 2

−16

could be found.

6.3 ZK-Crypt

ZK-Crypt is a stream cipher designed by Carmi Gres-

sel, Ran Granot and Gabi Vago. With a 128-bit key

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

264

and a 128-bit IV it is highly vulnerable to both bit-

ﬂipping and d-Monomial distinguishers. Biases with

P < 2

−96

were consistently found in bit-ﬂipping at-

tacks. In d-Monomial attacks the bias was in P <

−12

range, although in one case P < 2

−37

was ob-

served. A typical test run would involve 2

IV se-

tups.

6.4 POMARANCH

POMARANCH is a stream cipher designed by Cees

Jansen and Alexander Kolosha. With a 128-bit key

and a 112-bit IV it is susceptible to bit-ﬂipping tests

when the ﬂipping occurs at the end of the IV vector.

Biases with P < 2

−96

were consistently observed in

such attacks. Typical run would involve 2

IV se-

tups.

6.5 NLS and TSC-3

NLS is a stream cipher designed by Gregory Rose,

Philip Hawkes, Michael Paddon and Miriam Wiggers

de Vries. TSC-3 is a stream cipher proposed by Jin

Hong, Dong Hoon Lee, Yongjin Yeom, Daewan Han

and Seongtaek Chee.

These ciphers fall into “borderline category”.

Some strong biases were found, but not strong enough

to indicate a clear design ﬂaw. We suspect that im-

proved attacks are possible by hand-crafting the test

parameters to exploit particular features of the design

of these ciphers.

In NLS with a 128-bit key and a 128-bit IV, a bias

with P < 2

−20

was observed in one d-Monomial test

run of 2

IV setups. Multiple lesser d-Monomial bi-

ases occur in a consistent pattern.

In TSC-3 with a 160-bit key and a 128-bit IV, a bit

ﬂipping bias with P < 2

−18

was observed and lesser

biases occur in a consistent pattern.

7 CONCLUSION

We have discussed the application of Algebraic Nor-

mal Form and d-Monomial tests to chosen-IV attacks

against stream ciphers. It has been demonstrated that

these tests appear to be highly effective in distinguish-

ing “simple” Boolean functions as well as (rather sur-

prisingly) complex functions from random ones.

In an experiment with eSTREAM stream ciphers,

we found that the output of six of the 34 candidates

could be distinguished from random with our meth-

ods, with additional few being borderline cases and

requiring further investigation. Ciphers with poor

mixing properties even fail a simple bit-ﬂipping test

(or its ANF variant).

ACKNOWLEDGEMENTS

The author wishes to thank Keith Martin for his valu-

able comments. This research was supported by a

grant from Helsingin Sanomain 100-Vuotiss

ati

REFERENCES

Clote, P., Kranakis, E.: Boolean Functions and Computa-

tion Models. Springer-Verlag, 2002

Filiol, E.: A New Statistical Testing for Symmetric Ciphers

and Hash Functions. Proc. ICICS 2002, LNCS 2513,

Springer-Verlag 2002. pp. 342 – 353.

ECRYPT: The home page eSTREAM,

the ECRYPT Stream Cipher Project.

http://www.ecrypt.eu.org/stream/

Murphy, S.: The Power of NIST’s Statistical Testing of AES

Candidates. AES Comment to NIST, April 2000.

Rukhin, A. et al.: A Statistical Test Suite for Random and

Pseudorandom Number Generators for Cryptographic

Applications. NIST Special Publication 800-22 (re-

vised May 15, 2001)

Wegener, I.: The complexity of Boolean functions. Wiley-

Teubner series in computer science. Wiley, Teubner,

1987

CHOSEN-IV STATISTICAL ATTACKS ON eSTREAM CIPHERS

265

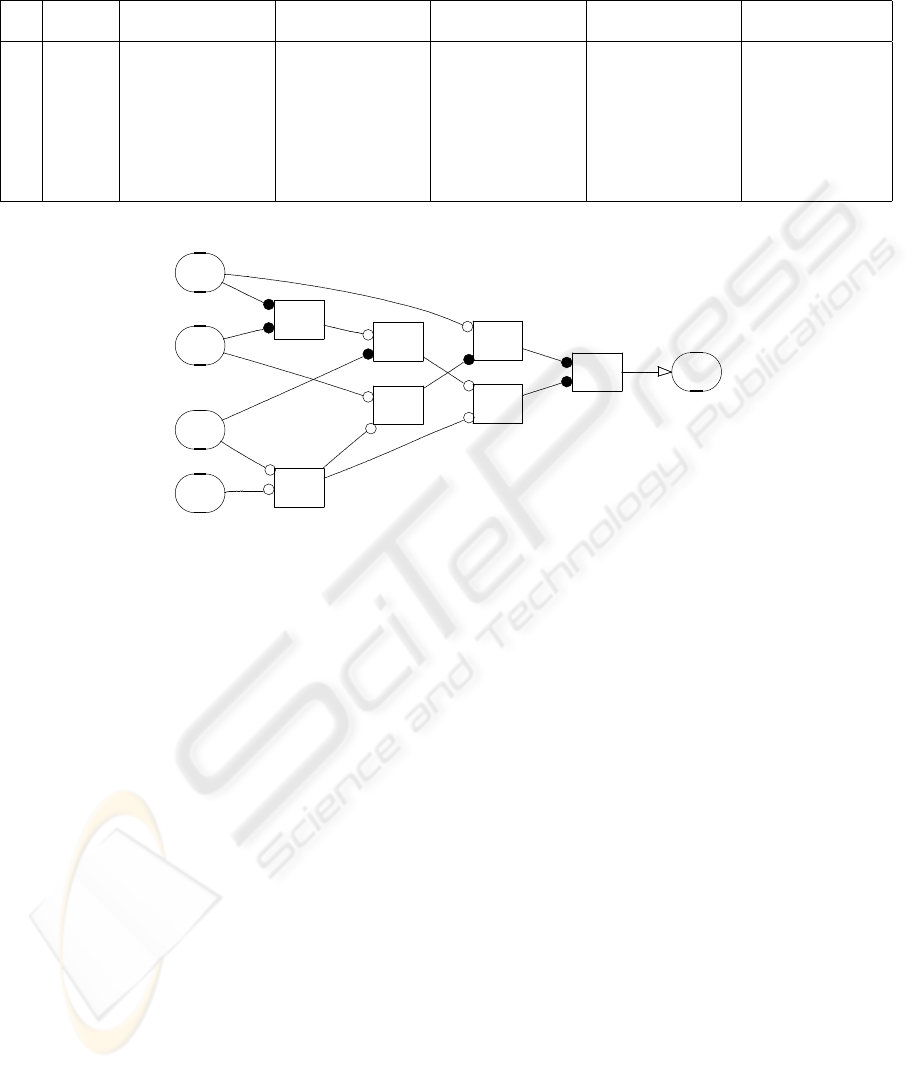
Table 1: Distribution of the 65536 four-bit Boolean functions by gate complexity and the results of d-monomial tests on

Boolean functions of given gate complexity.

d = 0 d = 1 d = 2 d = 3 d = 4

i G

i,0

i,1

i,2

i,3

i,4

0 6 1 0.167 4 0.167 0 0.000 0 0.000 0 0.000

1 64 34 0.531 76 0.297 48 0.125 0 0.000 0 0.000

2 456 228 0.50 0 648 0.355 672 0.246 256 0.140 0 0.000

3 2474 1237 0.500 3912 0.395 5136 0.346 3264 0.330 832 0.336

4 10624 5312 0.500 18960 0.446 26976 0.423 17536 0.413 4608 0.434

5 24184 12092 0.500 47888 0.495 71328 0.492 47616 0.492 13216 0.546

6 25008 12504 0.500 52992 0.530 83232 0.555 55744 0.557 12576 0.503

7 2720 1360 0.500 6592 0.606 9216 0.565 6656 0.612 1536 0.565

1 + x

+ x

∧

⊕

∧

Figure 2: An automatically generated picture of a Boolean function with gate complexity 7. In this picture a ﬁlled circle

indicates that the given input is inverted. This function can not be implemented with, say, six gates (regardless of the choice

of gates).

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

266