JASTEG2000

Steganography for JPEG2000 Coded Images

Domenico Introna, Francescomaria Marino

DEE, Politecinico di Bari, via Re David 200, 70125 Bari, Italy

Keywords: Data hiding, steganography, privacy, JPEG2000.

Abstract: The steganography is the concept of making invisible a communication, and not only incomprehensible its

content (as cryptography does). This is generally achieved hiding a secret message into another one

(“cover”), which appears as the only object of the communication.

This paper proposes a steganographic method employing JPEG2000 images as “cover”. It reaches high

embedding even introducing a low distortion.

Experimental results have shown up to 35%-45% embedding rate, with 2 dB of distortion (in the worst case)

at 0.5 bpp and 30%-40% with less than 4 dB at 1.0 bpp. Comparing these results with those achieved by

JPEG2000-BPCS, it can be seen that our method produces considerably less post-embedding growth and

distortion (in some case, they differ for more than 5 dB).

1 INTRODUCTION

The word steganography comes from two Greek

words: στεγανοσ (i.e., steganos=hidden) and

γραϕια (i.e., graphia=writing). The join of these

words describes the concept of a communication

which hides not only its contents, but also its

existence. This is well different from cryptography,

which makes incomprehensible the meaning of a

communication, though this one can be seen by

everybody.

Steganographic techniques, usually exploit a

second perceptible message (“cover”), having

disjoined meaning by the secret message. The cover

works as a “Trojan horse”, being a container of the

secret message (F.A.P. Petitcolas, et al., 1999; S.

Katzenbeisser and F. A. P. Petitcolas, 2000).

The new technologies and, in special way, the

Internet and the information networks, require more

and more sophisticated strategies in order to prevent

the message privacy. Even different steganographic

techniques have been presented in literature, which

are suitable for many media and standard coding

involved with the Internet, at the best of our

knowledge, only two steganographic algorithms

dealing with the emerging JPEG2000 image

standard coding (JPEG2000 website; M. D. Adams,

2001) have been proposed: the algorithm proposed

by Pochi-Su and C.-C. Jay Kuo, 2003 and

JPEG2000-BPCS (Bit-plane Complexity

Segmentation) by H. Noda et al., 2002.

These two state-of-the-art methods follow

different philosophies. Briefly, the method proposed

by Pochi-Su and C.-C. Jay Kuo has the goal of

keeping constant the size of the cover image file, pre

and post the embedding. As a consequence, it is

necessary bounded for what concerns the embedding

capacity. Conversely, JPEG2000-BPCS aims at

getting high capacity, even with a low distortion,

though it gives less importance to the eventual post-

embedding growth.

In this paper, we consider the features of the

JPEG2000 standard coding, and how they can be

exploited in order to efficiently hide information.

We therefore define a technique for deciding which

bits of a given codeblock (and not all of them

without distinction) may be used for the embedding,

and how such embedding can be “reversibly”

performed, i.e., allowing the receiver of correctly

recovering the hidden message.

We derive a flexible strategy which differentiates

the number of bits to be hidden into a coefficient

with respect to the absolute value of the same

coefficient, bounding (in a “someway relative”

sense) the introduced distortion. Its result is a high

embedding/low distortion steganographic method

which has been implemented in a software tool

329

Introna D. and Marino F. (2006).

JASTEG2000 - Steganography for JPEG2000 Coded Images.

In Proceedings of the International Conference on Security and Cryptography, pages 329-336

DOI: 10.5220/0002095403290336

 SciTePress

(JASTEG2000 website) and experimentally

evaluated. In the worst cases, it gets up to 35%-45%

embedding rate with approximately 2 dB of

distortion, and up to 30%-40% embedding rate with

less than 4 dB of distortion, when applied on

benchmarks coded at 0.5 bpp and 1.0 bpp,

respectively. These results outperform those

achieved by other existing methods. In particular, we

will show that our method produces much less post-

embedding growth, getting a considerably lower

distortion, than JPEG2000-BPCS.

2 JPEG2000 STANDARD

JPEG2000 is a powerful coding technique for still

images, standardized as ISO 15444 in 2001. It

achieves impressive compression ratios even holding

a good image quality, overcoming the classical

JPEG. The key of this performance are the wavelets,

which constitute, in JPEG2000, the counterpart of

the Discrete Cosine Transform (DCT) in JPEG.

Wavelets (S. G. Mallat, 1989) use complex base

functions, with some coarse features akin to sine

waves. They also contain some detailed features like

pulse codes, thereby creating a set of fuzzy pixels

with variable-sized features, as opposed to DCT's

one-size-fits-all sine waves. Other interesting

(sometimes innovative) features of JPEG2000 are:

- it offers both lossless and lossy coding;

- it allows of modifying and coding any region of

the image, directly working on the compressed data

stream;

- it introduces the concept of Region of Interest

(ROI) of an image;

- it allows a flexible bitstream ordering;

- it has an improved error resilience of the

codestream;

- it provides a localized random access into an

image;

- it grants an efficient and accurate rate control.

More in detail, the processing steps of JPEG2000

are:

(a) DC-Shifting

: This step is applied on the

components having only positive values. It shifts the

range of these components from [0, 2

-1] to [-2

n-1

+1,

n-1

], n being the number of bits used for that

component.

(b) Multi-Component Transform

: This step is

needed in case of color images. It un-correlates the

color components either into YUV space (in case of

lossless coding) or into YCbCr space (in case of

lossy coding).

: DWT is

the cornerstone of JPEG2000. The best way to

represent a signal using wavelets is to scan the entire

image for the “mother wave” that best represents

that particular image. However, this “mother wave”

would have to be attached to the image data, thereby

increasing the size of the compressed file. Instead,

JPEG2000 adopts an universal mother wave ahead

of time, eliminating the need to send it along with

the file. These ones are LeGall 5/3 (for lossless

coding) and Daubechies 9/7 (for “lossy” coding).

(d) Quantization

: Scalar and uniform

quantization is applied on DWT coefficients. The

standard does not specify thresholds values, since

these ones can be decided by the user, basing on the

particular case. Anyway, the standard proposes a

method for determining them.

(e) ROI Scaling

: This is an optional functionality

in which, the wavelet coefficients related to regions

that the user has indicated as “relevant” are scaled

up. By this way, these Regions Of Interest (ROI)

gain quality during the next coding steps.

(f) EBCOT (Tier 1)

: In JPEG 2000, coding is

performed in two steps (tiers). In tier 1, the

quantized coefficients of each subband are

partitioned into codeblocks. These ones are

independently coded using an Embedded Bit-planes

Coding with Optimized Truncation (EBCOT).

(g) EBCOT (Tier2)

: Tier 2 optimally truncates

the bit-stream of each codeblock minimizing the

distortion due to the bit-rate constraint. Firstly,

candidate truncation points are selected in the

convex hull of the rate-distortion curve. Afterward,

when some codeblocks are collected, and a statistic

is available, the truncation point is selected among

these candidates in order to minimize the distortion.

In JPEG2000, this step produces information loss,

as well as quantization.

3 A STEGANOGRAPHIC

METHOD FOR JPEG2000

When steganography is applied to classical codecs

(e.g., JPEG), the embedding is generally cascaded to

the quantization, since this one is the main (and

often, the unique) lossy step. Nevertheless, this

approach is unsuitable for JPEG2000. In fact, in this

standard, the quantized coefficients can successively

be truncated in EBCOT Tier 2 in order to match a

particular bit rate, that the user could have required.

Therefore, steganography when applied to

JPEG2000 cover images needs a “down-coding/up-

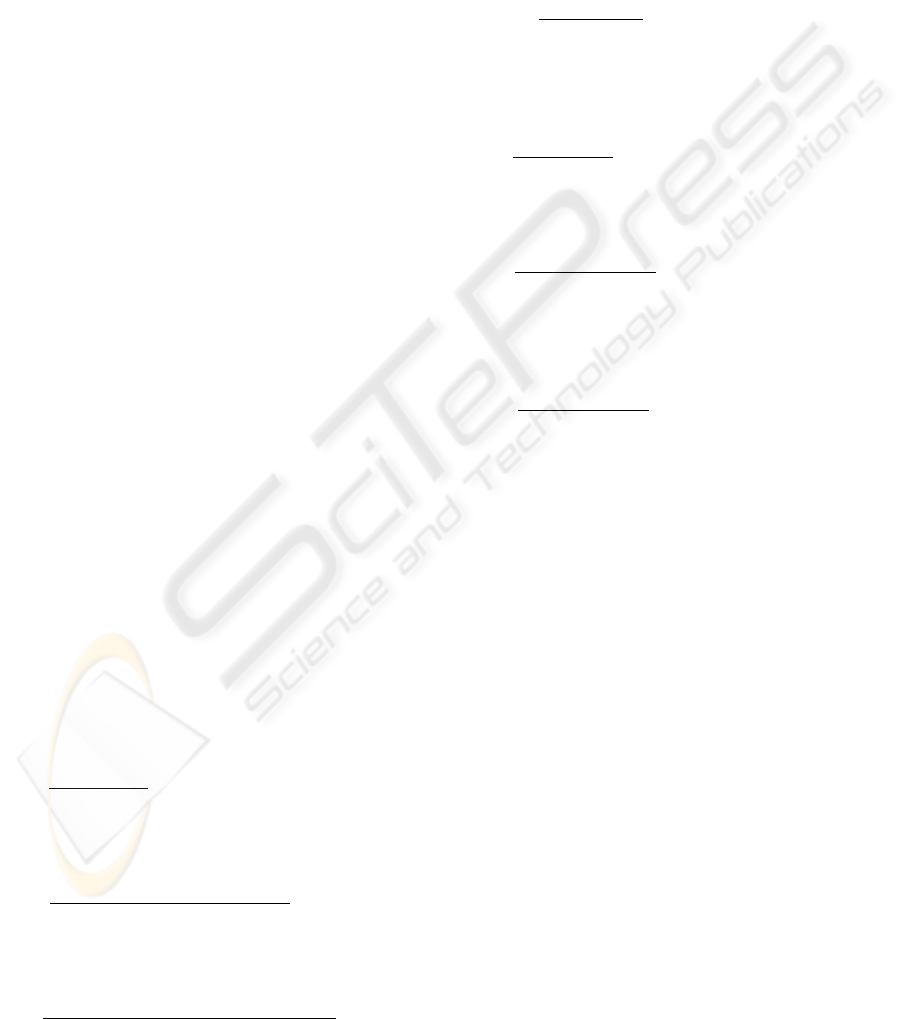
decoding” scheme, as that one shown in Fig. 1. In it,

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

330

and in the following, we will adopt the terms:

- CI, i.e., the Cover Image;

- SM, i.e., the Secret Message object of the

steganography;

- CICS, i.e., the Cover Image Code Stream (before

the embedding);

- MECS, i.e., the Message Embedding Code Stream

(after having embedded SM into CI).

COVER IMAGE

(CI)

”Hello

World!”

SECRET MESSAGE

(SM)

DC Shifting

MESSAGE-

EMBEDDING

CODE

STREAM (MECS)

(b)

MCT

(a)

DWT

(d)

Quantization

(c)

EBCOT Tier 1

(g)

EBCOT Tier 2

(f)

EBCOT Tier 1

EBCOT Tier 2

EBCOT Tier 1

(n)

EBCOT Tier 2

(without

rate-distortion)

(m)

(h)

(i)

Embedding

(k)

0010111

1100101

1010111

1101100

COVER IMAGE

CODE STREAM (CICS)

ROI Scaling

(e)

ROI Descaling

ROI Scaling

(l)

(j)

QUANTIZED &

TRUNCATED DWT

COEFFICIENTS

(

Matrix X

)

EMBEDDING

MESSAGE DWT

COEFFICIENTS

(Matrix X’)

QUANTIZED DWT

COEFFICIENTS

Figure 1: Steganographic approach to JPEG2000 cover

images.

Basically, a “cover image” is firstly coded in

JPEG2000 through steps (a)-(d), as described in

Section 2. After Quantization (d), for those cases

without bit-rate constraint (i.e., when the user has

not required any bit-rate, or when the final

achievable compression is not relevant), the

Embedding (k) can be directly performed, as

denoted by the dotted arrow, and the coding

completed through steps (l)-(n), taking care of do not

applying the rate distortion in step (n), since this

could truncate parts of the secret message.

Conversely, in case of bit-rate constraint, the

above mentioned “down-coding/up-decoding”

scheme is required. Steps (e)-(g) are carried out

(down-coding) in order to perform, in the EBCOT

Tier 2 (g), a bitplane truncation matching the

required bit-rate. These ones are then followed by

the up-decoding steps (h)-(j) which get newly back

the quantized and appositely truncated DWT

coefficients, to be used for the embedding in step

(k). Afterward, the final coding steps (l)-(n) are

performed, without applying now the rate distortion,

in step (n).

The embedding constitutes the soul of a

steganographic method. In particular, for JPEG2000,

this step should define: 1) how to select the bits to be

used as “hosts”, among those of the quantized and

truncated DWT coefficients, and 2) how to embed in

these host-bits the bits of the SM (making them

perfectly recoverable).

A fundamental feature of the proposed method is

constituted by its embedding technique. It not only

exploits the resolutions and the subbands which are

less sensible to the noise (as similar other

approaches do), but selects the number of secret bits

to be embedded into each coefficient, varying this

number on the base of the module of the related

coefficient: so doing, it “proportionally” corrupts

any coefficient. As a result, our method gets higher

PSNR than other steganographic methods, which

embed secret bits indifferently from the value of the

host-coefficients. Moreover, for what concerns the

strategy for selecting the host-bits, it has been

experimented in four different versions, providing

the user with four different compromises between

post-embedding growth and distortion. Because of

the space limitation, here only the "version 4" of the

method is described; details on the other versions of

the method can be retrieved on (JASTEG2000

website).

In the following, the above two issues are

discussed in detail.

3.1 Bits Embedding Technique

Let:

- α, a parameter input by the user and specifying the

maximum number of bits that might be potentially

modified in any DWT coefficient during the

embedding (obviously, higher α, higher the

embedding capacity and the introduced distortion);

- X, the matrix of the quantized and truncated DWT

coefficients x(i, j), constituting the input to the

Embedding step (k) in Fig. 1;

- PMS1 (|x(i, j)|), the Position of the Most

Significant “1” of |x(i, j)|, “0” being the position of

the LSB.

Therefore, for any non-zero coefficient x(i, j), we

can define the Position of the Most Significant

available Host Bit available for the embedding, as:

PMSHB(x(i,j)) = min{α-1, PMS1(|x(i,j)|-1)} (1)

In this scenario, the embedding in x(i, j) is

performed simply replacing the PMSHB(x(i, j))+1

least significant bits of x(i, j), with a same number of

bits of the secret message, getting a post-embedding

JASTEG2000 - Steganography for JPEG2000 Coded Images

331

value x'(i, j) to be coded (the coefficients ∈ {-1, 0,

1} having PMSHB(x)≤0 are not employed).

Note that since the embedding replaces the least

significant bits, the EBCOT Tier 2 in step (n) would

be performed without applying bit planes truncation,

as previously remarked. Because of this strategy, the

embedding modifies only the bits considered in the

refinement pass, leaving unaltered the other coding

passes. Moreover, because of (1), the number of bits

embeddable in x(i, j) –anyway, never more than α–

grows with |x(i, j)|, bounding –in a “someway

relative” sense– the introduced distortion.

In the recovering step, the receiver, knowing α

and reading x'(i, j), can easily determine PMS1(|x'(i,

j)|) and PMSHB(x'(i, j)). Afterwards, supposed:

PMSHB(x'(i, j))=PMSHB(x(i, j)) (2)

(the case of PMSHB(x'(i, j))≠PMSHB(x(i, j)) is

discussed later) the receiver can simply reconstruct

the secret message, collecting the less significant

bits of any x'(i, j), up to the bit in position

PMSHB(x'(i, j)).

For the sake of clarity, examples of

embedding/recovering of secret bits 10010

into {-13,

4}, are provided in the following (α=4):

Embedding:

x=(-13)

=(11110011)

2-complement

; |x|=00001101;

PMS1(|x|)=3; PMSHB(x)=2 => 3 bits (100) can be

embedded up to the position 2; this generates:

x' =(11110001

)

2-complement

=(-15)

to be coded;

x=(4)

=(00000100)

2-complement

; |x|=00000100;

PMS1(|x|)=2; PMSHB(x)=1 => 2 bits (10

) can be

embedded up to the position 1; this generates:

x' =(00000101

)

2-complement

=(5)

to be coded;

Recovering:

x'=(11110001)

2-complement

=(-15)

; |x'|=00001111;

PMS1(|x'|)=3; PMSHB(x')=2 => 3 bits can be

recovered up to the position 2: 100

x'=(00000101)

2-complement

=(5)

; |x'|=00000101;

PMS1(|x'|)=2; PMSHB(x')=1; => 2 bits can be

recovered up to the position 1: 10

Recovered message: 10010

Nevertheless, even (2) holds for positive values

of x(i, j), particular sequences of embedded bits (i.e.,

either a sequence of all '0' or a sequence of all '1'),

might modify negative values of x(i, j) into values

x'(i, j) causing:

PMSHB(x'(i, j)) ≠ PMSHB(x(i, j)) (3)

which is the negation of (2).

Obviously, these values, if effectively coded,

will generate an incorrect message recovering. This

is better evidenced by the following examples where

the secret bits 001111

are embedded into {-6, -16},

causing an incorrect recovering:

x=(-6)

=(11111010)

2-complement

; |x|=00000110;

PMS1(|x|)=2; PMSHB(x)=1; after having

embedded 00

: x' =(11111000)

2-complement

=(-8)

;

x=(-16)

=(11110000)

2-complement

; |x|=00010000;

PMS1(|x|)=4; PMSHB(x)=3; after having

embedded 1111

: x' =(11111111)

2-complement

=(-1)

;

Recovering (in this case it will result incorrect):

x'=(11111000)

2-complement

=(-8)

; |x'|=00001000;

PMS1(|x'|)=3; PMSHB(x')=2; => 3 bits are

supposed to be recovered up to the position 2: 000

x'=(11111111)

2-complement

=(-1)

; |x'|=00000001;

PMS1(|x'|)=0; PMSHB(x')=-1; => 0 bits are

supposed to be recovered, i.e., this coefficient

appears to be unused during the embedding.

Erroneously recovered message: 000

Therefore, in all the cases verifying (3), a post-

processing of x'(i, j) is needed in order to assure a

correct message recovering. This is made

complementing the bit of x'(i, j) in position

PMSHB(x(i, j))+1, by this way, getting a new value

verifying (2). It is worth to note that this correction

is carried out during the embedding, by the

“sender”, which well knows PMSHB(x). For the

sake of clarity, the examples previously considered

became (after being post-processed):

x'=(11111000)

2-complement

; after complementing

the bit in position 2: x'=(11111100

) with

PMSHB(x')=1;

x'=(11111111)

2-complement

after complementing the

bit in position 4: x'=(11101111

) with PMSHB(x')=3;

As a proof of the effectiveness of the introduced

corrections, it can be seen that now PMSHB(x')≡

PMSHB(x), that will allow a perfect recovering.

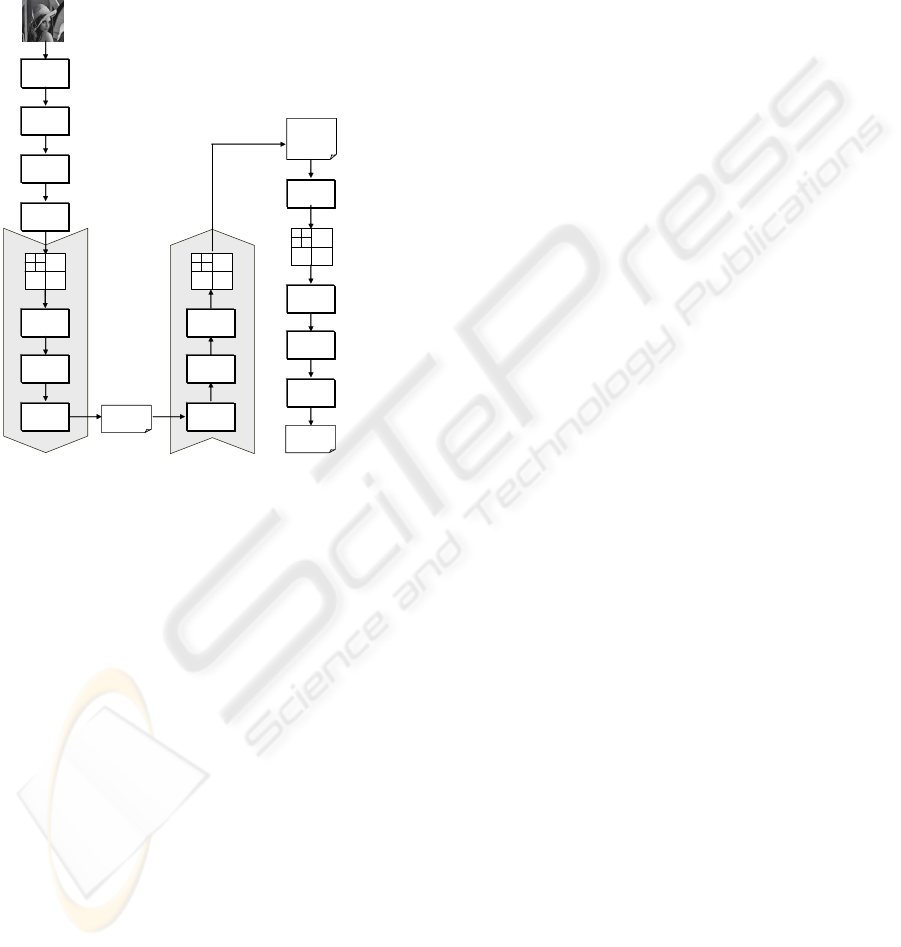
3.2 Bits Selection Strategy

The "version 4" of our method selects the

coefficients x(i, j) starting from the HH orientation at

the highest resolution, and continues as denoted by

the order shown in Fig. 2.

Figure 2: “Vertical” bits embedding (decomposition in 3

levels of DWT with 4 bitplanes. NU=Not Used).

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

332

0. From the CI, build X, the matrix of coefficients, through the steps (a)-(j) of

Fig. 1.

1. create and initialize a second matrix X' = X;

2. while (there are secret bits to be embedded) AND (host-bits are available) do

3. select a subband S according to the given order (Fig. 2);

4. consider the next coefficient x(i, j) into subband S, according to a given

scanning path;

5. given α, evaluate PMS1(|x(i, j)|) and PMSHB(x(i, j));

6. modify x’(i, j) by replacing its PMSHB(x(i, j))+1 less significant bits

with secret bits;

7. discard the just embedded PMSHB(x(i, j))+1 bits of the secret message;

8. if PMSHB(x'(i, j)) ≠ PMSHB(x(i, j))

9. correct x’(i, j) by complementing its bit in position PMSHB(x(i, j))+1;

10. end while;

11. if (there are secret bits to be yet embedded) do

12. output “SECRET MESSAGE TOO LONG – EMBEDDING NOT COMPLETED

RETRY INCREASING EITHER α OR THE BIT RATE OF THE COVER IMAGE”

13. exit;

14. end if;

15. apply steps (l)-(n) of Fig. 1 on X’ without bit planes truncation;

16. end.

(a)

0. From the MECS, obtain X' performing the reverse EBCOT Tier2, reverse EBCOT

Tier1 and ROI Descaling;

1. while there are secret bits to be recovered do

2. select a subband S according to the given order (Fig. 2);

3. consider the next coefficient x(i, j) into subband S, according to a given

scanning path;

4. given α, evaluate PMS1(|x'(i, j)|) and PMSHB(x'(i, j));

5. collect the PMSHB(x'(i, j))+1 less significant bits of x'(i, j) into the

recovered message;

6. end while;

7. output the recovered message;

8. end.

(b)

Figure 3: Pseudo code. Message embedding (a); message recovering (b).

As soon as a coefficient x(i, j) is considered, all

its PMSHB(x(i,j))+1 least significant bits are

replaced in a “vertical” fashion (i.e., along any bit

plane) by a same number of secret bits, as shown by

the arrows, starting from the least significant one.

Pseudo code of this version of our

steganographic method is given in Fig. 3. In Fig. 3.a,

lines 2-10 perform the embedding. The subband S in

line 3 is selected according to the order shown in

Fig. 2. The coefficient x(i,j) is selected into S in line

4 according to any pre-established scanning path

(raster or what ever); an additional possibility might

be that one of discarding the pixels belonging to

region of interest in order to do not deteriorate them

during the embedding. Lines 11-13 terminate the

procedure, sending a warning, in case the embedding

cannot be completed because the available host-bits

are less than the secret bits to be embedded.

4 EXPERIMENTAL RESULTS

In order to evaluate HELD, we have implemented

the software tool “JASTEG2000”. JASTEG2000 is a

visual environment whose name is two-fold: 1) it is

a tribute to the well known freeware JASPER

(Jasper website), that we have used for developing

the codec; 2) it recalls its main goal:

“STEGanography for JPEG2000 cover images”.

We have experimentally conducted some studies,

in order to examine the post-embedding growth rate

and distortion, using as benchmarks three well-

known 512x512 pixels images (“Barbara”, “Lena”

and “Mandrill”). “Barbara” and “Lena” are grey-

scale images at 8bpp; “Mandrill” is a true-color

image at 24bpp.

These tests are described in paragraphs 4.1 and

4.2, respectively. Afterward, a comparative analysis,

using as terms of comparison the other

JASTEG2000 - Steganography for JPEG2000 Coded Images

333

steganographic approaches to JPEG2000 available in

literature is reported.

4.1 Growth Rate

A first experiment evaluates the impact of the

embedding in terms of growth of MECS, measuring

the Growth Rate, defined as:

%100

size CICS

size CICS-size MECS

⋅=RateGrowth

(4)

We randomly generated a sequence of bits

(constituting the SM) and performed different tests,

increasing, test after test, the amount of information

to be hidden. Though the optimal value of α (i.e., the

maximum number of host-bits per coefficient)

should be tentatively found for each cover image

and at any bit rate, we reduced the degrees of

freedom, using α=4 for the entire set of tests, after

having verified that this choice represented a good

compromise between embedding capacity and

introduced distortion.

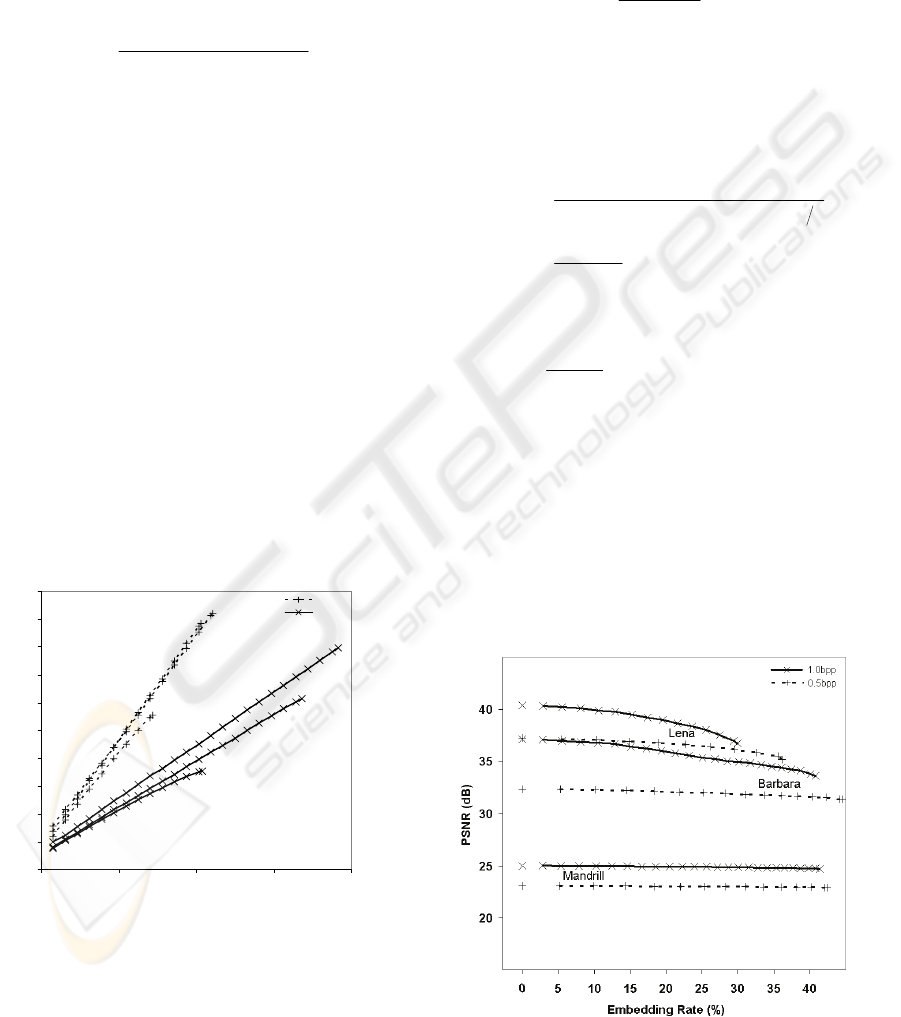
Fig. 4 shows the results of this experiment. It

reports the “Growth Rate vs Embedded kbits”

characteristics obtained by steganography performed

onto the test images coded both at 0.5 and at 1.0

bpp, with 6 DWT resolutions, and after having

applied the component transform on the colour

image “Mandrill”.

It is evident that the shown characteristic well

fits a linear trend which makes our method

particularly attractive, since the effect of the growth

rate can be easily predicted.

100

0 50 100 150 200

Embedded Message (kbit)

Growth Rate (%)

0.5bpp

1.0bpp

Lena

Barbara

Mandrill

Lena

Barbara

Mandrill

Figure 4: Growth Rate vs Embedded Message for

Mandrill, Barbara and Lena coded at 0.5 and 1.0 bpp.

4.2 Post-Embedding Distortion

A second experiment focused on the distortion

introduced by the steganography onto the cover

images. In order to produce measures comparable

with those reported by their authors for JPEG2000-

BPCS, we have considered the “PSNR vs the

Embedding Rate” characteristic.

In this context, the Embedding Rate evaluates the

integration of SM inside CI, and it is defined as:

%100

sizeCICS

sizeSM

⋅=RateEmbedding

(5)

while PSNR measures the quality loss of the

message-embedding image with respect to the cover

image (i.e., the image itself, before the embedding),

and it is defined (for colour and grey scale,

respectively) as:

()

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

)(

255

log10

3)()()(

255

log10

YMSE

BMSEGMSERMSE

PSNR

(6)

with:

()

∑∑

−

cjiPcjiP

cMSE

),,(),,('

)(

(7)

where MxN is the size of the image, in pixels; and

P(i, j, c) and P'(i, j, c) are the numerical values of the

pixel (i, j) for the component c, before and after the

embedding, respectively.

This experiment was conducted measuring

PSNR and Embedding Rate in each one of the

incremental test conducted in the previous

experiment. The obtained results are shown in Fig.

5, where the points with embedding rate = 0 denote

the quality loss due to the only compression.

Figure 5: PSNR vs Embedding Rate for Mandrill, Barbara

and Lena coded at 0.5 and 1.0 bpp.

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

334

We can observe that the PSNR, though slightly

decreasing at higher embedding rates, remains

almost constant in Mandrill, since it varies (in the

considered interval of embedding rate: 0%-45%) in a

range of only 0.16 dB and of 0.31 dB, for the coding

at 0.5 bpp and 1.0 bpp, respectively. Conversely, a

more perceptible decrement in the PSNR is visible

for the images Barbara coded at 0.5 bpp (≅1 dB:

from 32.34 dB at 0% down to 31.37 dB at 45%), and

more pronouncedly for Lena coded at 0.5 bpp (≅2

dB: from 37.23 dB at 0% down to 35.15 dB at 36%).

Instead, the curves related to Barbara and Lena

(coded at 1.0 bpp) decrease according to a slightly

convex and almost linear trend.

Concluding, in order to provide an evaluation

even from a perceptive point of view, we show in

Fig. 6 the test image Lena (the worst benchmark, in

the sense of PSNR) in case of an embedding rate

Figure 6: Steganography onto Lena coded at 1.0 bpp

(Embedding rate=30%). pre (top) and post the embedding

(bottom).

of 30% (coding at 1.0 bpp). It can be seen that the

introduced distortion is not perceptible with respect

to the quality loss already caused by the

compression.

4.3 Comparative Analysis

Only two other steganographic algorithms have

already been proposed for JPEG2000: JPEG2000-

BPCS (H. Noda et al. 2002) and the method

proposed by Po-Chyi Su and C.-C.J. Kuo, 2003.

It is worth to note that method by Po-Chyi Su

and C.-C.J. Kuo follows a philosophy completely

different from our method. In fact, its main goal

consists of holding constant the size of the code

stream after the embedding (size of MECS = size of

CICS). Consequently, it allows good embedding

capacity only at high bit-rates. Due to these different

features, in this comparative analysis it is considered

only for the sake of completeness.

Conversely, JPEG2000-BPCS, rather than

holding constant the size of the code stream, aims at

preserving a high PSNR, even getting a high

embedding capacity. Its goal is the same of the

algorithm proposed in this paper. Therefore, the

comparison of our method vs JPEG2000-BPCS is

more significant.

1) growth rate: The only available data for what

concerns the growth rate reached by JPEG2000-

BPCS are 29.8% and 32.8% caused when 2412

bytes and 7332 bytes are embedded into Barbara in

case of coding at 0.5bpp and at 1.0bpp, respectively.

These ones are well higher than those of our method

(22.4% and 24.9%) at the same conditions.

As previously said, no growth (for any allowed

dimension of the embedded message) is generated

by the method by Po-Chyi Su and C.-C.J. Kuo, since

it has been conceived appositely aiming at this goal.

2) post-embedding distortion: In Fig. 7 the

characteristics of the steganographic algorithm

proposed by Po-Chyi Su and C.-C.J. Kuo are

reported. They have been obtained thanks to Dr. Po-

Chyi Su, that has kindly provided the software

implementing his method. As already said, this

method does not allow high embedding rate at 1.0

bpp (only 6.8% for Lena and 3.4% for Barbara).

Moreover, it decreases the PSNR, much faster than

JPEG2000-BPCS and our method do. It pays this

price in order to achieve a post-embedding “growth

0”.

A more significant comparison can be performed

with respect to JPEG2000-BPCS. In Fig. 8 we

propose the “PSNR vs Embedding Rate” diagram,

related to the performance of JPEG2000-BPCS, as it

was reported by their authors. Comparing this figure

JASTEG2000 - Steganography for JPEG2000 Coded Images

335

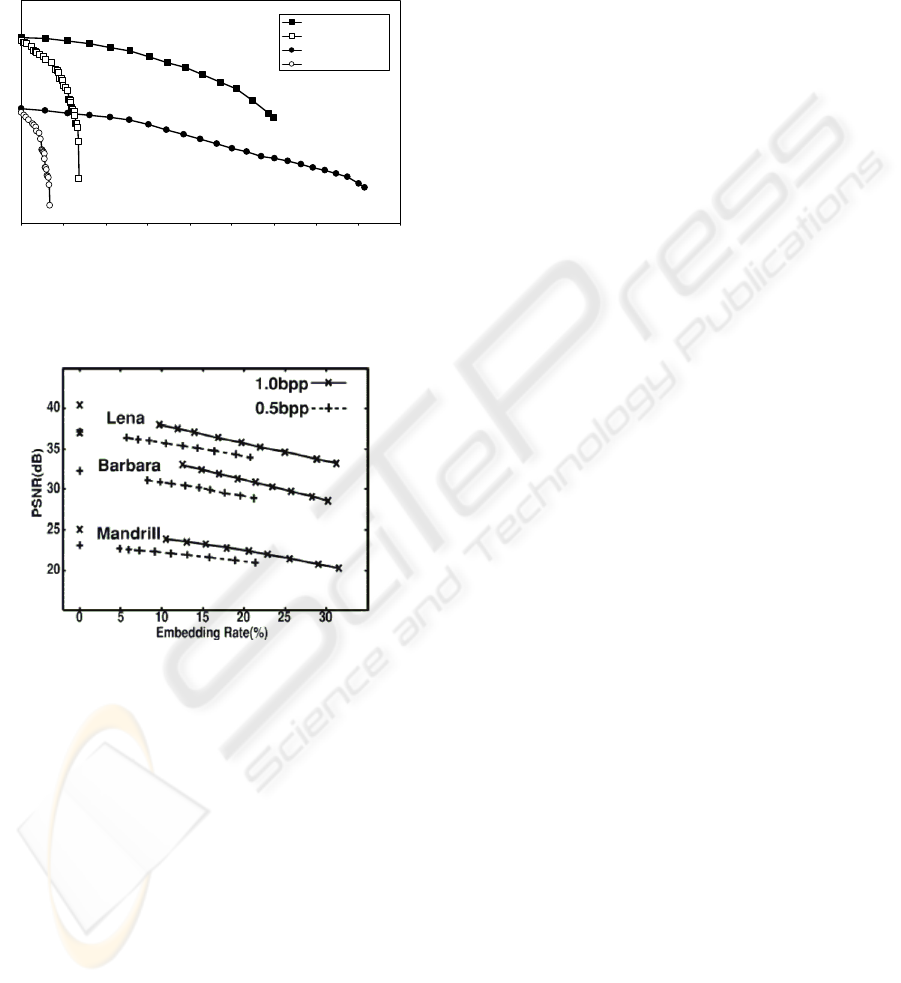
with the Fig. 5, it can be seen that, for any test

image, our method performs significantly better than

JPEG2000-BPCS, inducing much lower distortion

(in some case, more than 5 dB), and getting higher

embedding rates than those reported in Fig. 8 for

what concerns the images coded at 0.5 bpp.

0 5 10 15 20 25 30 35 40 45

Em bedding Rate [%]

PSNR [dB]

Lena - Our Method

Lena - Po Chyi Su

Barbara - Our Method

Barbara - Po Chyi Su

Figure 7: PSNR vs Embedding Rate in case of

steganography by our method and by Po-Chyi Su and C.-

C.J. Kuo Algorithm, performed onto Lena and Barbara

coded at 1.0 bpp.

Figure 8: PSNR vs Embedding Rate in case of

steganography by JPEG2000-BPCS, as shown in (H. Noda

et al., 2002).

5 CONCLUSION

A new steganographic algorithm, suited for

JPEG2000 cover images, has been introduced. It is

based on an embedding technique that, not only

corrupts the resolutions that are less sensitive to the

noise, but also determines the number of bits to be

embedded into a single DWT coefficient, basing on

its magnitude.

This particular feature results in a low “relative”

distortion. Its performances reachable by these four

versions have been experimentally analyzed using

well known benchmarks, and the post-embedding

growth and distortion measured.

In particular, up to 35%-45% embedding rate

with approximately 2 dB of distortion in the worst

cases (for the benchmarks coded at 0.5 bpp), and up

to 30%-40% embedding rate with less than 4 dB of

distortion in the worst cases (for coding at 1.0 bpp)

have resulted. Moreover, for what concerns the

growth of the codestream, it gets a very interesting

feature: it performs linearly, making the effect of

this phenomenon easily predictable.

The proposed method has been compared also

with other existing steganographic methods suited

for the JPEG2000 standard, in particular with

JPEG2000-BPCS, which similarly to our method,

aims at getting high embedding, introducing low

distortion. The comparison has put in result that our

method:

- produces considerably less growth;

- gets higher embedding rates at low bit rate coding;

- induces lower distortion (in some case, it differs

from JPEG2000-BPCS for more than 5 dB).

ACKNOWLEDGEMENTS

The authors would thank Dr. Pochyi-Su (National

Central University, Taiwan) for having kindly

provided the source code of his steganographic

method.

REFERENCES

F.A.P. Petitcolas, R.J. Anderson and M.G. Kuhn, 1999.

Information Hiding – A Survey. Proceedings of the

IEEE, vol.87, no.7, pp. 1062-1078.

S. Katzenbeisser and F. A. P. Petitcolas, 2000. Information

Hiding Techniques for Steganography and Digital

Watermarking. Norwood, MA: Artech House.

JPEG2000 website: http://www.jpeg.org/JPEG2000.html

M. D. Adams, 2001. The JPEG-2000 still image

compression standard. ISO/IEC JTC 1/SC 29/WG 1,

Tech. Rep.

Po-Chyi Su and C.-C.J. Kuo, 2003. Steganography in

JPEG2000 compressed images. IEEE Transactions on

Consumer Electronics, V. 49, N. 4, p. 824-832.

H. Noda, J. Spaulding, M.N. Shirazi and E. Kawaguchi,

2002. Application of bit-plane decomposition

steganography to JPEG2000 encoded images. IEEE

Signal Processing Letters, V. 9, N. 12, pp. 410-413.

JASTEG2000 website: http://dee.poliba.it/dee-web/

marinoweb/JASTEG2000.html

S. G. Mallat, 1989. A theory for multiresolution signal

decomposition: The wavelet representation. IEEE

Trans. Pattern Anal. Machine Intell., vol. 2, Dec., pp.

674–693.

Jasper website: http://www.ece.uvic.ca/~mdadams/jasper/

SECRYPT 2006 - INTERNATIONAL CONFERENCE ON SECURITY AND CRYPTOGRAPHY

336