
OPTIMAL POWER ALLOCATION IN A MIMO-OFDM TWISTED
PAIR TRANSMISSION SYSTEM WITH FAR-END CROSSTALK
Andreas Ahrens, Christoph Lange
Institute of Communications Engineering, University of Rostock
Richard-Wagner-Str. 31, 18119 Rostock, Germany
Keywords:
Twisted-pair Cable, OFDM, Power Allocation, Multiple-Input Multiple-Output System, Lagrange Multiplier
Method, Singular-Value Decomposition.
Abstract:
Crosstalk between neighbouring wire pairs is one of the major impairments in digital transmission via multi-
pair copper cables, which essentially limits the transmission quality and the throughput of such cables. For
high-rate transmission, often the strong near-end crosstalk (NEXT) disturbance is avoided or suppressed and
only the far-end crosstalk (FEXT) remains as crosstalk influence. If FEXT is present, signal parts are trans-
mitted via the FEXT paths from the transmitter to the receiver in addition to the direct transmission paths.
Therefore transmission schemes are of great practical interest, which take advantage of the signal parts trans-
mitted via the FEXT paths. Here a SVD (singular-value decomposition) equalized MIMO-OFDM system
is investigated, which is able to take advantage of the FEXT signal path. Based on the Lagrange multiplier
method an optimal power allocation schema is considered in order to reduce the overall bit-error rate at a fixed
data rate and fixed QAM constellation sizes. Thereby an interesting combination of SVD equalization and
power allocation is considered, where the transmit power is not only adapted to the subchannels but rather to
the symbol amplitudes of the SVD equalized data block. As a result it can be seen that the exploitation of
FEXT is important for wireline transmission systems in particular with high couplings between neighbouring
wire pairs and the power allocation is possible taking the different subcarriers into account.
1 INTRODUCTION
OFDM (orthogonal frequency division multiplex) is a
widely accepted transmission schema in both, wire-
line and wireless transmission. Examples include
digital subscriber line (DSL) (Bingham, 2000), Eu-
ropean digital video broadcast (DVB), digital audio
broadcast (DAB) and wireless local area networks
(WLAN) such as 802.11a and HIPERLAN/2. A lot
of publications have been published in the literature
where the resilience of multicarrier transmission sys-
tems against the delay spread was highlighted, provid-
ing a sufficient guard interval length (Bingham, 2000;
van Nee and Prasad, 2000).
In a multiuser scenario considered here, a resilience
against intersymbol interference (ISI) isn’t sufficient
to fulfill given quality criteria. In local cable net-
works, crosstalk is one of the most limiting dis-
turbances (Valenti, 2002). Since the NEXT is a
very strong disturbance several techniques have been
developed in order to avoid or suppress it (Honig
et al., 1990). In this case only the FEXT remains as
crosstalk influence. Often optical fibre transmission is
used up to a building’s entrance and the last few hun-
dred metres within the building are bridged by cop-
per cables. For such short cables used in high-data
rate systems in the local cable area, the FEXT is par-
ticularly strong (Valenti, 2002) and as a result heavy
multiuser interference arise. This has lead to a great
interest in transmission systems which are capable to
take such disturbances into account.
In different publications, e.g, in (Lange and
Ahrens, 2005), it was theoretically shown, that gains
are possible by FEXT exploitation. In this contribu-
tion an interesting approach for the practical exploita-
tion of the FEXT signal parts is presented: On each
wire pair the multicarrier technique OFDM (Hanzo
et al., 2000) is used and in addition the mutual impact
of the wire pairs in a cable binder via far-end crosstalk
is taken into account. Therefore the n-pair cable
is modelled as a (n, n) MIMO transmission system
and the combination of singular-value decomposition
(SVD) and optimal power allocation using the La-
grange Multiplier method is considered with the aim
164
Ahrens A. and Lange C. (2006).
OPTIMAL POWER ALLOCATION IN A MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEM WITH FAR-END CROSSTALK.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 164-169
DOI: 10.5220/0001568001640169
Copyright
c
SciTePress
of a bit-error minimization at a given data rate. Con-
trary to other publications considering a similar topic,
here the focus lies on the combination of singular-
value decomposition and power allocation. Thereby
the optimal power allocation solution is presented for
given boundary conditions (fixed QAM constellation
size and limited total transmit power).
The remaining part of this contribution is organized
as follows: Section 2 introduces the cable charac-
teristics and the considered system model including
the MIMO-OFDM transmission systems with SVD-
based equalization. In section 3 possible optimiza-
tion objectives for MIMO transmission systems are
discussed and the underlying optimization criteria are
briefly reviewed. In section 4 the transmit power al-
location scheme is explained and in section 5 the ob-
tained results are presented and discussed. Finally,
section 6 provides some concluding remarks.
2 SYSTEM MODEL
The distorting influence of the cable on the wanted
signal is modelled by the cable transfer function
G
k
(f) = e
−l
j
f
f
0
, (1)
where l denotes the cable length (in km) and
f
0
represents the characteristic cable frequency (in
MHz · km
2
) (Kreß and Krieghoff, 1973).
The far-end crosstalk coupling is covered by the
transfer function G
F
(f) with
|G
F
(f)|
2
= K
F
· l · f
2
, (2)
whereby K
F
is a coupling constant of the far-end
crosstalk, which depends on the cable properties such
as the type of isolation, the number of wire pairs and
the kind of combination of the wire pairs within the
binders (Valenti, 2002).
The considered cable binder consists of n wire
pairs and therefore a (n, n) MIMO transmission sys-
tem arises. The mapping of the transmit signals
u
s µ
(t) onto the received signals u
k µ
(t) (with µ =
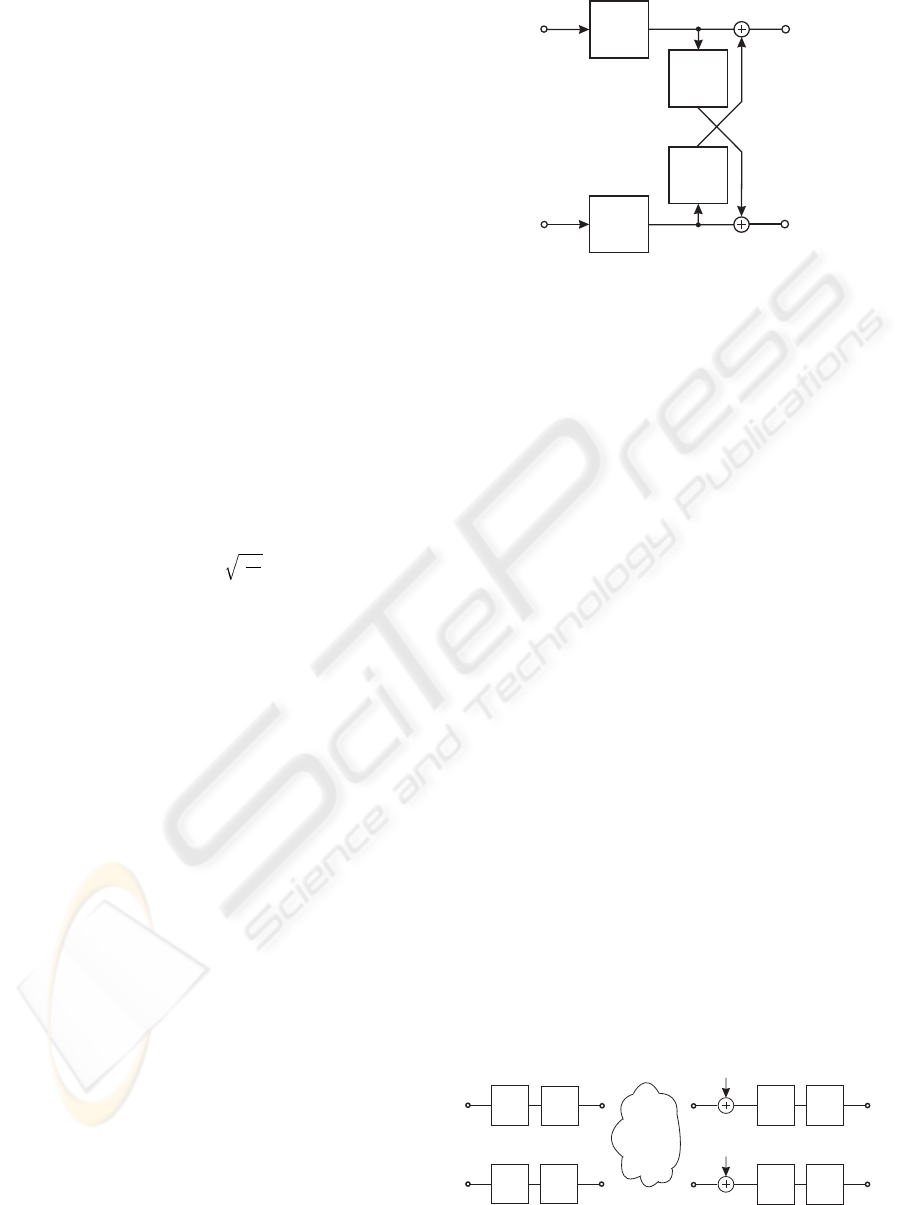
1, . . . , n) can be described accordingly to Fig. 1.
On each wire pair of the cable binder OFDM
(orthogonal frequency division multiplexing) is used
as transmission technique to combat the effects of
the frequency-selective channel (Bahai and Saltzberg,
1999; Bingham, 2000). In such a (n, n)-MIMO-
OFDM system, an N -point IFFT (N subchannels)
has to be performed on every wire pair. By inserting
a guard interval (GI) in front of the transmit signal
and removing it at the receiver side an interchannel
interference (ICI) and intersymbol interference (ISI)
free transmission can be established, assuming that
the length of the GI is longer than the temporal ex-
tension of the channel impulse response (van Nee and
u
s 1
(t)
u
s 2
(t)
u
k 1
(t)
u
k 2
(t)
G
k
(f)
G
k
(f)
G
F
(f)
G
F
(f)
Figure 1: MIMO cable transmission model system with
FEXT (n = 2).
Prasad, 2000). After removing the GI at the receiver
an N-point FFT has to be performed. The arising sys-
tem model is depicted in Fig. 2.
The kth data block a
µ
[k] of the length n
b
= N
transmitted by the wire pair µ (with µ = 1, . . . , n) is
denoted by
a
µ
[k] = (a
1 µ
[k], a
2 µ
[k], . . . , a
N µ
[k])
T
(3)
and results in a received vector (µ = 1, . . . , n)
u
µ
[k] = (u
1 µ
[k], u
2 µ
[k], . . . , u
N µ
[k])
T
. (4)
To get an adequate system model, it is necessary to
rearrange the symbols of the data vector a
µ
[k] (with
µ = 1, . . . , n) defined in (3). Combining all symbols
which are transmitted via the same subcarrier in one
vector results in
e
a
κ
[k] = (a
κ 1
[k], . . . , a
κ µ
[k], . . . , a
κ n
[k])
T
. (5)
Stacking all subcarriers in one vector leads to
e
a[k] =
e
a
T
1
[k], . . . ,
e
a
T
κ
[k], . . . ,
e
a
T
N
[k]
T
, (6)
where
e
a
κ
[k], defined in (5), contains all symbols
which are transmitted via the subcarrier κ. Therefore
(6) contains all symbols which are transmitted in one
time slot simultaneously since n
b
equals N.
After removing the GI at the receiver side a N-
point FFT has to be performed and leads to the re-
ceived vector similarly to (6)
e
u[k] =
e
u
T
1
[k], . . . ,
e
u
T
κ
[k], . . . ,
e
u
T
N
[k]
T
, (7)
a
1
.
.
.
a
n
u
1
.
.
.
u
n
u
s 1
(t)
u
s n
(t)
u
k 1
(t)
u
k n
(t)
IFFT
IFFT
FFT
FFT
GI
GI
GI
−1
GI
−1
MIMO
cable
n
1
(t)
n
n
(t)
Figure 2: MIMO-OFDM cable transmission model.
OPTIMAL POWER ALLOCATION IN A MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEM WITH
FAR-END CROSSTALK
165

where
e
u
κ
[k] contains the ISI- and ICI-free receive
symbols of the subcarrier κ. However
e
u
κ
[k] still con-
tains the crosstalk between neighboring wire pairs on
each subcarrier. Due to the GI this vector has the same
length as the data vector defined in (6).
Additionally a white Gaussian noise n
µ
(t) (with
µ = 1, 2, . . . , n) with power spectral density Ψ
0
is
assumed, which results after receive filtering in the
vector n and can be defined similar to (7) as
n[k] =
n
T
1
[k], . . . , n
T
κ
[k], . . . , n
T
N
[k]
T
. (8)
Thereby it is assumed that the noise components are
independently from each other, which can be justified
by the rectangular shape of the receive filter functions.
The block oriented transmission system description
is given by
e
u = R ·
e
a + n . (9)
The matrix R has a block diagonal structure
R =
R
1
0 ··· 0
0 R
2
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 ··· R
N
. (10)
In equation (10) zero-matrices are denoted by 0 and
for the matrices R
κ
(with κ = 1, . . . , N) the follow-
ing syntax is used
R
κ
=
r
(κ)
1 1
··· r
(κ)
1 n
.
.
.
.
.
.
.
.
.
r
(κ)
n 1
··· r
(κ)
n n
, (11)
with the elements describing the couplings of the data
symbols on the subchannel κ. Based on the symme-
try of the considered transmission system r
(κ)
ν µ
(for
ν = µ) can be determined taking the FFT of g
k
(t) =
F
−1
{G
k
(f)} into account. The elements r
(κ)
ν µ
(for
ν 6= µ) consider the coupling between neighbouring
wire pairs and can be ascertained calculating the FFT
of g
k fn
(t) = F
−1
{G
F
(f) · G
k
(f)}. The κth value
of this vector represents r
(κ)
ν µ
. The elements r
(κ)
ν µ
(for
ν 6= µ) are assumed to be identical for each κ, al-
though in practical systems the coupling between the
wire pairs is slightly different and it depends on their
arrangement in the binder (Valenti, 2002).
The remaining interferences on each subcarrier can
now be eliminated by an efficient equalization strat-
egy. A popular strategy is represented by the singular
value decomposition (SVD), which can be done on
each subcarrier separately. The SVD of the matrix
R
κ
can be written as
R
κ
=
e
U
κ
·
e
V
κ
·
f
W
H
κ
, (12)
where
e
U
κ
and
f
W
H
κ
are unitary matrices and
e
V
κ
is a
real diagonal matrix (Kovalyov, 2004).
The rearranged data vector
e
a
κ
(5) is multiplied by
the matrix
f
W
κ
and results in the transmit data vector
e
b
κ
. The received vector
e
u
κ
= R
κ
·
e
b
κ
+ n
κ
is multi-
plied by the matrix
e
U
H
κ
. Thereby neither the transmit
power nor the noise power is enhanced. The over-
all transmission relationship for the subcarrier κ (with
κ = 1, . . . , N) is defined as
e
y
κ
=
e
U
H
κ
·
e
u
κ
=
e
U
H
κ
·
R
κ
·
f
W
κ
·
e
a
κ
+ n
κ
=
e
V
κ
·
e
a
κ
+
e
U
H
κ
· n
κ
. (13)
3 OPTIMIZATION OBJECTIVES
AND QUALITY CRITERIA
Current signal processing strategies for MIMO sys-
tems typically fall into two categories: data through-
put maximization at a given transmission quality or
bit-error rate minimization at a fixed data rate. In this
contribution we have restricted ourselves to the BER
minimization at a fixed data rate. Thereby optimal but
highly complex or suboptimal solutions with reduced
complexity can be found, e.g. (Krongold et al., 2000;
Jang and Lee, 2003; Park and Lee, 2004; Ahrens and
Lange, 2006).
The signal-to-noise ratio (SNR) is a reasonable per-
formance criterion for noise-dominated scenarios. A
signal-to-noise ratio
̺ =
(Half vertical eye opening)
2
Disturbance Power
=
(U
A
)
2
(U
R
)
2
(14)
is often defined as a quality parameter (Kreß et al.,
1975) with the half vertical eye opening U
A
and the
noise disturbance power U
2
R
per quadrature compo-
nent. Between the signal-to-noise ratio ̺ = U
2
A
/U
2
R
and the bit-error probability in the general case of M-
ary quadrature amplitude modulation (QAM) the in-
terrelationship
P
f
=
2
ld(M)
1 −
1
√
M
erfc
r
̺
2
(15)
holds (Kalet, 1987; Proakis, 2000). The SVD-based
equalization on each subcarrier leads to a different
half vertical eye opening
U
(ε)
A
=
p
ξ
ε
· U
s
(16)
for each data symbol. Here, U
s
denotes the half-level
transmit amplitude and
√
ξ
ε
are the positive square
roots of the eigenvalues of the matrix R
H
κ
R
κ
, de-
scribing the distortions on each subcarrier. Further-
more, each symbol of the data vector a is disturbed
by a noise with identical disturbance power in the
SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA
APPLICATIONS
166

quadrature components, which is assumed to be un-
correlated with power U
2
R
each. The bit-error proba-
bility per symbol for QAM is defined as
P
f µ
=
2
ld(M)
1 −
1
√
M
erfc
U
(µ)
A
√
2 U
R
!
.
(17)
The aggregate bit-error probability
P
f
=
1
N
b
N
b
−1
X
µ=0
P
f µ
(18)
is derived by averaging over the error probabilities of
all N
b
= n · n
b
symbols of the data block, since all
eye openings occur with the same probability.
4 POWER ALLOCATION
The half vertical eye opening of each symbol posi-
tion is weighted by the factor
√
p
µ
and therefore all
eye openings of the data block are in general different
from each other. Assuming an identical noise power
for all symbol positions, the symbol positions with the
smallest half vertical eye openings dominate the bit-
error rate. Here a transmit power partitioning scheme
would be necessary in order to minimize the overall
bit-error rate under the constraint of a limited total
transmit power.
In a power allocation scheme each symbol of the
data block is weighted by a real factor
√
p
µ
. This
setup leads to the half vertical eye opening
U
(µ)
A,PA
=
√
p
µ
·
p
ξ
µ
· U
s
(19)
per symbol. The power allocation evaluates the half-
level amplitude U
s
of the µth symbol by the factor
√
p
µ
. This causes in general a modified transmit am-
plitude U
s
√
p
µ
for each symbol of the transmit data
vector and the signal constellation changes. Together
with the noise disturbance per quadrature component
a BER per symbol and block can be calculated:
P
f µ
=
2
1 −
1
√
M
ld(M)
erfc
r
p
µ
ξ
µ
2
·
U
s
U
R
!
.
(20)
The aggregate bit-error probability per block yields
P
f
=
2
1 −
1
√
M
ld(M) N
b
N
b
−1
X
µ=0
erfc
r
p
µ
ξ
µ
2
·
U
s
U
R
!
.
(21)
In the subchannels of the multicarrier system inves-
tigated in this contribution M-ary square QAM with
transmit power (Proakis, 2000)
P
s QAM
=
2
3
U
2
s
(M − 1) (22)
is used (Proakis, 2000). Using a parallel transmission
over N subchannels the overall mean transmit power
per wire yields to
P
s
= N · P
s QAM
= N
2
3
U
2
s
(M − 1) , (23)
and results in a total transmit power of n P
s
by taking
n wire-pairs into account.
Considering now generally different half-level am-
plitudes U
s
√
p
µ
after power allocation on the symbol
layers, it follows
P
s µ
=
√
p
µ
2
·
2
3
U
2
s
(M − 1) = p
µ
2
3
U
2
s
(M − 1)
(24)
for the µth symbol position.
If now a block of N
b
data symbols, transmitted
over N parallel subchannels per wire pair, is ana-
lyzed with these generally different half-level ampli-
tudes U
s
√
p
µ
after power allocation, the mean trans-
mit power of the block becomes
P
s,PA
= n N
2
3
U
2
s
(M − 1)
1
N
b
N
b
−1
X
µ=0
√
p
µ
2
.
(25)
From the requirement
P
s,PA
− n P
s
= 0 (26)
that the overall mean transmit power for the whole
binder consisting of n wire pairs is limited to n P
s
it
follows, that the auxiliary condition
n N
N
b
P
s QAM
N
b
−1
X
µ=0
√
p
µ
2
− n N P
s QAM
= 0
N
b
−1
X
µ=0
p
µ
− N
b
= 0
(27)
has to be maintained.
In order to find the optimal
√
p
µ
the Lagrange mul-
tiplier method is used (Park and Lee, 2004; Ahrens
and Lange, 2006). Contrary to other publications,
here the power allocation has not been carried out
on each subcarrier independently from each other,
although this might be possible. To consider the
subcarrier specific distortions (e. g. increasing cable
attenuation with increasing subcarrier indices) in a
best possible way, here all subcarrier singular val-
ues are combined in one vector, in order to smooth
out the distortions. The Lagrangian cost function
J(p
0
, ··· , p
N
b
−1
) may be expressed as
J(···) =
A
N
b
N
b
−1
X
µ=0
erfc
r
p
µ
ξ
µ
2
·
U
s
U
R
!
+λ·B
N
b
,
(28)
OPTIMAL POWER ALLOCATION IN A MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEM WITH
FAR-END CROSSTALK
167
with the Lagrange multiplier λ (Park and Lee, 2004)
and
A =
2
ld(M)
1 −
1
√
M
. (29)
The parameter B
N
b
in (28) describes the boundary
condition
B
N
b
=
N
b
−1
X
µ=0
p
µ
− N
b
= 0 (30)
following from (27). Differentiating the Lagrangian
cost function J(p
0
, ··· , p
N
b
−1
) with respect to the
p
µ
and setting it to zero, leads to the optimal set of
power allocation coefficients. As solution for the p
µ
we get (a computer algebra system such as MAPLE or
MATLAB can come in handy)
p
µ
=
1
ξ
µ
U
2
R
U
2
s
W
A
2
ξ
2
µ
2 π N
2
b
λ
2
U
4
s
U
4
R
!
, (31)
where W(x) describes the Lambert W function (Cor-
less et al., 1996). The parameter λ can be calcu-
lated by insertion of (31) in (30) and numeric analysis.
With calculated λ the optimal p
µ
can be determined
using (31).
Power allocation with lower complexity can be
achieved by suboptimal methods, which can on the
one hand rely on an approximation for the erfc(x)
function or which ensure on the other hand equal
signal-to-noise ratios per symbol (Ahrens and Lange,
2006).
5 RESULTS
The FEXT impact is in particular strong for short ca-
bles (Valenti, 2002). Therefore for numerical analy-
sis an exemplary cable of length l = 0.4 km with
n = 10 wire pairs is chosen. The wire diameter is
0.6 mm and hence a characteristic cable frequency of
f
0
= 0.178 MHz · km
2
is assumed. On each of the
wire pairs a multicarrier system with N = 10 sub-
carriers was considered. The actual crosstalk circum-
stances are difficult to acquire and they vary from ca-
ble to cable. Therefore a mean FEXT coupling con-
stant of K
F
= 10
−13
(Hz
2
·km)
−1
is exemplarily em-
ployed (Valenti, 2002; Aslanis and Cioffi, 1992). The
average transmit power on each wire pair is supposed
to be P
s
= 1 V
2
and as an external disturbance a
white Gaussian noise with power spectral density Ψ
0
is assumed. Identical systems on all wire pairs were
presumed (multicarrier symbol duration T
s
= 2 µs,
M-ary QAM, a block length of n
b
= 10 and a guard
interval length of T
g
= T
s
/2). Furthermore, the base-
band channel of the multicarrier system is excluded
from the transmission in order to provide this fre-
quency range for analogue telephone transmission.
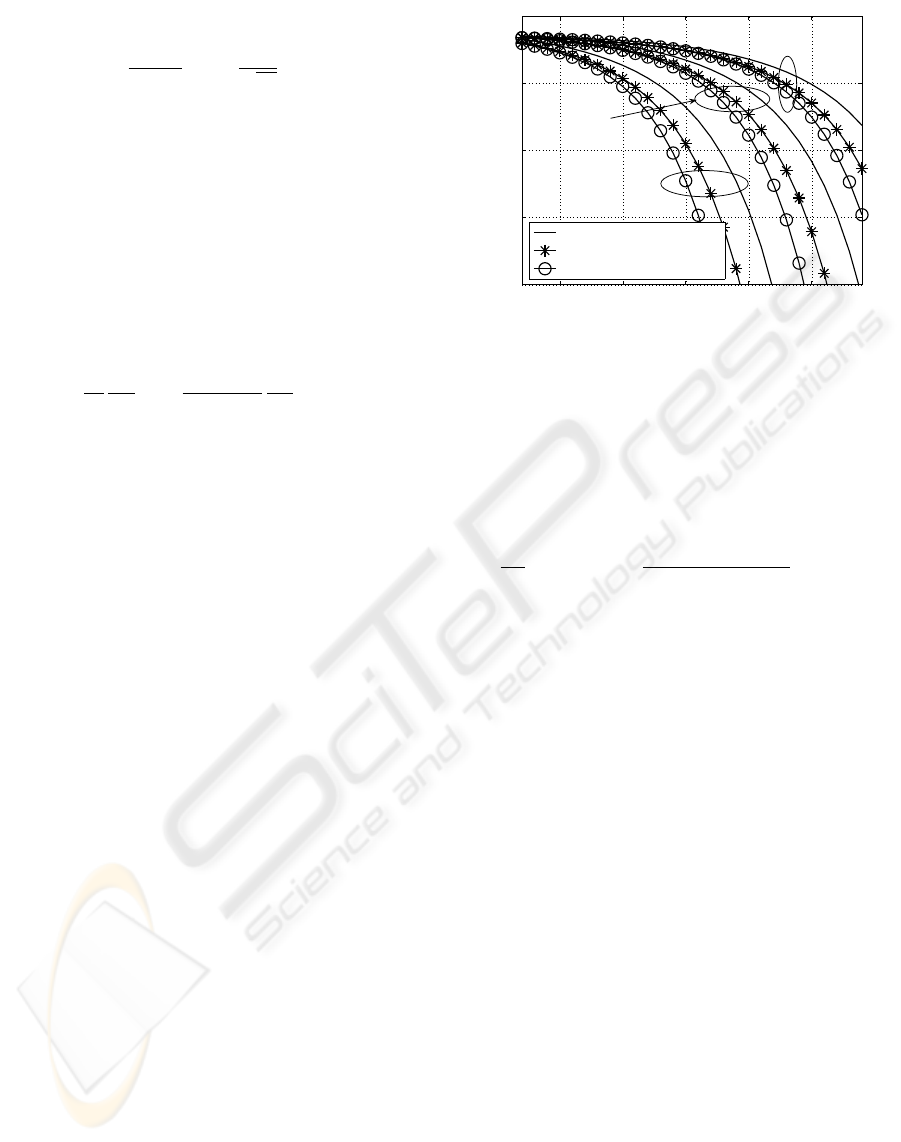
10 15 20 25 30
10
−8
10
−6
10
−4
10
−2
10
0
M = 4
M = 16
M = 64
10 · lg(E
s
/Ψ
0
) (in dB) →
bit-error rate →
SISO-OFDM without PA
MIMO-OFDM without PA
MIMO-OFDM with PA
Figure 3: BER comparison analyzing SISO-OFDM (n =
1) and MIMO-OFDM (n = 10, K
F
= 10
−13
(Hz
2
·
km)
−1
) with and without PA for different QAM constel-
lation sizes.
For a fair comparison the ratio of symbol energy
to noise power spectral density at the cable output is
defined for the MIMO case (n > 1) according to
E
s
Ψ
0
= (T
s
+ T
g
)
P
k
+ (n − 1)P
k fn
Ψ
0
, (32)
with
P
k
= P
s QAM
· T
s
+∞
Z
−∞
|G
s
(f) · G
k
(f)|
2
df (33)
and
P
k fn
= P
s QAM
·T
s
+∞
Z
−∞
|G
s
(f)·G
k
(f)·G
F
(f)|
2
df .
(34)
Thereby it is assumed, that the mean transmit power
tends to P
s QAM
and G
s
(f) is the transmit filter trans-
fer function describing the OFDM pulse shaping. The
results are depicted in Fig. 3 with the QAM constel-
lation sizes M as parameter. For purposes of sim-
plicity and in order to obtain meaningful results, the
QAM constellation sizes are chosen to be equal in all
subchannels of the multicarrier systems. This seems
to be reasonable in the example considered here,
since short cables do not have very strong frequency-
selective characteristics. For general cable transmis-
sion the optimization of bit loading with low com-
plexity in the MIMO context remains open for fur-
ther investigations. Furthermore it seems to be worth
mentioning that in case of different QAM constella-
tion sizes M also different overall bit rates can be
achieved. This could be used for an adaptation of
the bit rate to the user’s needs. In case of MIMO-
OFDM the signal parts, which are transmitted via the
SIGMAP 2006 - INTERNATIONAL CONFERENCE ON SIGNAL PROCESSING AND MULTIMEDIA
APPLICATIONS
168

FEXT paths are no longer disturbance: Now they are
exploited as useful signal parts. Therefore the trans-
mission quality is improved compared to the SISO-
OFDM case (OFDM transmission over a (fictive) per-
fectly shielded single wire pair). Similar results are
known from MIMO radio transmission with multi-
ple transmit and/or receive antennas, where multi-
ple transmission paths are exploited, too (Raleigh and
Cioffi, 1998; Raleigh and Jones, 1999).
The results show that under severe FEXT influ-
ence it is worth taking the FEXT signal paths into
account (Fig. 3). At small FEXT couplings no sig-
nificant gains are possible by MIMO-OFDM without
PA compared to a perfectly shielded wire pair (SISO-
OFDM), because the FEXT coupled signal parts are
very small. The results in Fig. 3 show further the po-
tential of appropriate power allocation strategies. The
absolut achievable gains depend on the actual cable
type and on the isolation of the wire pairs.
6 CONCLUSION
In this contribution, the practical exploitation of the
FEXT paths for improving the signal transmission
quality was investigated in terms of an exemplary
multicarrier transmission system on a symmetric cop-
per cable. It was shown, that the MIMO-OFDM cable
transmission enables gains in the BER performance
especially under severe FEXT influence. Thereby it
could be shown that power allocation is necessary to
achieve a minimum bit-error rate. In the exemplary
system considered here some restrictions were made,
which directly lead to some open points for further
investigations: In order to use MIMO-OFDM for ca-
bles of any length the most important open point is
the optimization of bit loading in combination with
the power allocation in the MIMO-OFDM context.
REFERENCES
Ahrens, A. and Lange, C. (2006). Transmit Power Alloca-
tion in SVD Equalized Multicarrier Systems. Inter-
national Journal of Electronics and Communications
(AE
¨
U), 60. accepted for publication.
Aslanis, J. T. and Cioffi, J. M. (1992). Achievable Infor-
mation Rates on Digital Subscriber Loops: Limiting
Information Rates with Crosstalk Noise. IEEE Trans-
actions on Communications, 40(2):361–372.
Bahai, A. R. S. and Saltzberg, B. R. (1999). Multi-Carrier
Digital Communications – Theory and Applications of
OFDM. Kluwer Academic/Plenum Publishers, New
York, Boston, Dordrecht, London, Moskau.
Bingham, J. A. C. (2000). ADSL, VDSL, and Multicarrier
Modulation. Wiley, New York.
Corless, R. M., Gonnet, G. H., Hare, D. E. G., Jeffrey, D. J.,
and Knuth, D. E. (1996). On the Lambert W Function.
Advances in Computational Mathematics, 5:329–359.
Hanzo, L., Webb, W. T., and Keller, T. (2000). Single- and
Multi-carrier Quadrature Amplitude Modulation. Wi-
ley, Chichester, New York, 2 edition.
Honig, M. L., Steiglitz, K., and Gopinath, B. (1990). Multi-
channel Signal Processing for Data Communications
in the Presence of Crosstalk. IEEE Transactions on
Communications, 38(4):551–558.
Jang, J. and Lee, K. B. (2003). Transmit Power Adapta-
tion for Multiuser OFDM Systems. IEEE Journal on
Selected Areas in Communications, 21(2):171–178.
Kalet, I. (1987). Optimization of Linearly Equalized
QAM. IEEE Transactions on Communications,
35(11):1234–1236.
Kovalyov, I. P. (2004). SDMA for Multipath Wireless Chan-
nels. Springer, New York.
Kreß, D. and Krieghoff, M. (1973). Elementare Ap-
proximation und Entzerrung bei der
¨
Ubertragung von
PCM-Signalen
¨
uber Koaxialkabel. Nachrichtentech-
nik Elektronik, 23(6):225–227.
Kreß, D., Krieghoff, M., and Gr
¨
afe, W.-R. (1975).
G
¨
utekriterien bei der
¨
Ubertragung digitaler Signale. In
XX. Internationales Wissenschaftliches Kolloquium,
Nachrichtentechnik, pages 159–162, Ilmenau. Tech-
nische Hochschule.
Krongold, B. S., Ramchandran, K., and Jones, D. L.
(2000). Computationally Efficient Optimal Power Al-
location Algorithms for Multicarrier Communications
Systems. IEEE Transactions on Communications,
48(1):23–27.
Lange, C. and Ahrens, A. (2005). Channel Capacity of
Twisted Wire Pairs in Multi-Pair Symmetric Copper
Cables. In Fifth International Conference on Informa-
tion, Communications and Signal Processing (ICICS),
pages 1062–1066, Bangkok (Thailand).
Park, C. S. and Lee, K. B. (2004). Transmit Power Alloca-
tion for BER Performance Improvement in Multicar-
rier Systems. IEEE Transactions on Communications,
52(10):1658–1663.
Proakis, J. G. (2000). Digital Communications. McGraw-
Hill, New York, 4 edition.
Raleigh, G. G. and Cioffi, J. M. (1998). Spatio-Temporal
Coding for Wireless Communication. IEEE Transac-
tions on Communications, 46(3):357–366.
Raleigh, G. G. and Jones, V. K. (1999). Multivariate
Modulation and Coding for Wireless Communication.
IEEE Journal on Selected Areas in Communications,
17(5):851–866.
Valenti, C. (2002). NEXT and FEXT Models for Twisted-
Pair North American Loop Plant. IEEE Journal on
Selected Areas in Communications, 20(5):893–900.
van Nee, R. and Prasad, R. (2000). OFDM for wireless
Multimedia Communications. Artech House, Boston
and London.
OPTIMAL POWER ALLOCATION IN A MIMO-OFDM TWISTED PAIR TRANSMISSION SYSTEM WITH
FAR-END CROSSTALK
169
