REAL-TIME LABEL INSERTION IN LIVE VIDEO THROUGH

ONLINE TRIFOCAL TENSOR ESTIMATION

Robert Lagani

ere

School of Information Technology and Engineering

University of Ottawa

Johan Gottin

Ecole Sup

erieure d’Ing

enieurs d’Annecy

Annecy, FRANCE

Keywords:

Augmented reality, trifocal tensor transfer, automatic labelling.

Abstract:

We present an augmented reality application that can supplement a live video sequence with virtual labels

associated with the scene content captured by an agile video camera moving inside an explored environment.

The method proposed is composed of two main phases. First, a matching phase where reference images are

successively compared with the captured images. And, second, a tracking phase that aims at maintaining the

correspondence between a successfully matched reference image and each frame of a captured sequence. La-

bels insertion is based on projective transfer using the trifocal tensor, this one being estimated and continuously

updated as the camera is moved inside the scene.

1 INTRODUCTION

Augmented reality (AR) is the technique of choice

when one wants to supplement a user’s view with

useful information concerning an observed scene.

Among the many ways by which content aware in-

formation can be added to a video sequence, adding

text annotations is probably one of the simplest but

effective way to proceed. Under this mode, some of

the scene objects are associated with informative texts

that are overlaid on the video when these objects be-

come visible. The displayed information often con-

sists in text labels pointing to the object’s parts they

describe. Such system would be particulary useful to

a mobile user exploring an unfamiliar environment.

Using a simple PDA equipped with a camera, or a

more sophisticated HMD, virtual overlays would ap-

pear on the images collected by the device, helping

the user in understanding the scene content. A possi-

ble use scenario is the case of a tourist visiting an art

gallery and for whom the supplemented labels would

provide information about the exhibited objects. Al-

ternatively, the system could assist a technician in the

inspection of a given building; the added virtual la-

bels would then represent a source of complementary

information (such as inventory numbers, ownership,

etc.) to help him in the accomplishment his tasks.

The augmented reality application presented here

is an automatic annotation system that can insert, at

frame rate, virtual labels associated with the scene

content captured by an agile video camera that freely

moves inside an explored environment. The core of

this application relies on an online-tensor estimation

scheme that has been presented in (Li et al., 2004)

and that has proven to be effective in AR. In this lat-

ter application, virtual objects are added to a scene

by transferring a virtual marker from two reference

views to the current view. We use here the same con-

cept to transfer labels from reference views to a video

frame with the difference that multiple reference im-

ages are now used. Also, a matching phase has been

introduced to detect when the current video is visu-

alizing scene elements for which textual annotations

are available and to identify the reference frames on

which this information has been entered. The method

proposed here is therefore composed of two phases.

First, this matching phase where the reference images

are successively compared with a current frame. And,

second, a tracking phase where the correspondence

between a successfully matched reference image and

each frame of the captured sequence is maintained.

An important asset of the proposed method is that it

doesn’t require estimation of the camera pose, neither

the use of some external localization sensor or the re-

course to some special markers inserted, beforehand,

inside the scene. Labels insertion is based on projec-

tive transfer using the trifocal tensor, this one being

estimated and continuously updated as the camera is

435

Laganière R. and Gottin J. (2006).

REAL-TIME LABEL INSERTION IN LIVE VIDEO THROUGH ONLINE TRIFOCAL TENSOR ESTIMATION.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 435-441

DOI: 10.5220/0001377504350441

 SciTePress

moved inside the scene. The estimation scheme we

have developed demonstrates that it is possible to ob-

tain quick and reliable estimates of the trifocal tensor.

A simple tracker is used to provide an evolving set

of point triplets. Stable performance of tracking over

long video sequences is also ensured through the au-

tomatic recovering of lost points and the removal of

wrong traces using trifocal transfer.

The next section brieﬂy reviews some existing sys-

tems while Section 3 presents the trifocal tensor. Sec-

tions 4 and 5 describe the proposed online labelling

procedure. Section 6 explains our online tensor esti-

mation scheme. Results of video frame augmentation

are presented in Section 7. Section 8 is a conclusion.

2 RELATED WORKS

Most of the existing automatic scene annotation sys-

tems rely on the use of positional sensors in order to

determine user’s 3D position and viewing direction.

In addition, an accurate model, describing the cur-

rent position of the objects of interest, is also required.

This is the case of the system in (Newman et al., 2001)

that uses ultrasonic pulses that are read by receivers

located at ﬁxed position in the ceiling. Accurate 3D

position is then obtained from times-of-ﬂight calcula-

tion. The objective of the augmented reality system in

(Bell et al., 2002) is to provide a situation-awareness

aid to a user in the form of a world in miniature repre-

sentation of the environment and that is embedded in

the user’s view. By selecting speciﬁc objects, either

in the scene image or in the virtual miniature repre-

sentation, pop-up annotations are displayed.

General real-time AR systems can also be used for

virtual label insertion. In the calibration-free system

described in (Kutulakos and Vallino, 1998), four or

more non-coplanar points are tracked along the video

and an afﬁne object representation is used to over-

lay virtual objects on a video stream. However, the

used control points have to be visible in every frame,

which restricts the range of views in which augmen-

tations can take place. The method in (Lourakis and

Argyos, 2004) is able to recover the camera positions

in close to real-time through the chaining of homogra-

phies computed from the tracking of 3D planes. The

AR system proposed in (Chia et al., 2002) computes

camera pose by using the epipolar constraints that ex-

ists between every video frame and two keyframes.

An alternative method consists in linking the video

frames with two keyframes; trifocal tensor is then

computed to transfer the location of the virtual ob-

ject from the keyframes (Boufama and Habed, 2005).

Another recent system that performs very well in real

time scene augmentation is the one proposed in (Vac-

chetti et al., 2004). In addition to keyframes, the

system also needs a 3D model of the target object.

By matching the current frame with a preregistered

keyframe, 2D-3D correspondences are obtained using

which virtual augmentation can be performed.

These approaches generally necessitate full calibra-

tion information, including all camera projection ma-

trices associated to the selected keyframes. AR sys-

tems not requiring any metric information would be

more ﬂexible and easier to deploy. This is the solu-

tion proposed by the application described here.

3 THE TRIFOCAL TENSOR

The augmented reality system proposed here relies

on projective geometry concepts, well-known in com-

puter vision, and that describes the relation between

the multiple views of a same scene. In particular,

the trifocal tensor which is a mathematical entity de-

scribing three-view geometry. It can represented by a

3×3×3 matrix T. This one can be computed from at

least 5 correspondences over the three views. The key

beneﬁt brought by this tensor matrix resides in the fact

that if a match (x, x



) is already known between the

ﬁrst two images, the position of the matching point x



in the third image can be determined exactly using:



= x



k=1

kjl

− x



k=1

kil

(1)

which deﬁnes 9 trilinearities for i, j ∈{1, 2, 3},4of

which are linearly independent. In the context of au-

tomatic label insertion, this means that if the tensor

relation between two reference images and a current

view can be maintained, then the labels speciﬁed in

these reference views can be transferred to the cur-

rent frame at their appropriate locations. This is the

strategy that is exploited here.

In the case of two views only, the projective relation

is described by a 3 × 3 matrix, the fundamental ma-

trix. This one deﬁnes an epipolar constraint that states

that the homolog of any point will necessarily lies on

a line (the epipolar line of that point) in the other view.

One use of this constraint is to validate putative match

pairs by verifying if the proposed matched point in-

deed lie on the corresponding epipolar lines. Note

that the trifocal tensor can also be used to validate

triplet of matches. Indeed, the trilinear constraint (1)

is always satisﬁed for good matches.

Tensor estimation and point transfer are used by

the online label insertion process. Guided matching

and match validation based on fundamental and ten-

sor matrices are used during the label speciﬁcation

phase as explained in the sections to follow.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

436

4 LABEL SPECIFICATION

The initial phase consists in specifying label locations

on the reference images. In order to be able to transfer

these labels on arbitrary views, it is required to specify

each of them on at least two reference views. How-

ever, since the tensor estimation process requires a set

of good matched points, three views of each object of

interest are used as it is the most favorable conﬁgura-

tion to obtain reliable feature matching.

The reference images are captured by moving a

camera at three different locations. Points are de-

tected in the ﬁrst image and as the camera is moved

from location 2 and 3, these points are tracked from

frame to frame (we used here the Lucas-Kanade

tracker). The points successfully tracked from the ﬁrst

reference image to the third one constitute an initial

match set that can then be validated and reﬁned. To do

so, we use an approach that combines the RANSAC

projective procedure described in (Roth and White-

head, 2000) and the calibrated matching procedure

proposed in (Vincent and Lagani

ere, 2002). The net

result is therefore three reference images for which a

rich and reliable set of matched triplets is available.

This pool of matches will be used during the online

label insertion procedure.

The interactive label insertion procedure can then

be undertaken using these three reference images.

Each label is inserted by ﬁrst specifying its location

in one reference image. Its location on a second refer-

ence image is then speciﬁed, but this time guided by

the epipolar geometry (computed from the available

match set), as shown in Figure 1. The location of the

label in the third image does not have to be speciﬁed,

as this one can be computed by virtue of the trifocal

tensor transfer property.

Once all the labels, for each object of interest have

been inserted, the live video augmentation application

can be launched.

5 ONLINE LABEL INSERTION

When the application is running, images are continu-

ously acquired using a camera that is freely moved

inside the scene. The online label insertion proce-

dure is composed of two phases: a matching phase,

where references images are compared with the video

frames in order to determine which labels have to be

inserted, and a tracking phase that allows to keep dis-

playing the labels at their appropriate locations. The

complete process is described in Figure 2.

Figure 1: Speciﬁcation of the virtual labels in reference im-

age 1 (top) and guided insertion (i.e. the associated point

must be on the epipolar line shown) of ’redial’ label in the

second reference image (bottom).

5.1 The Matching Phase

Ideally, each of the captured frame should be com-

pared with all the stored reference images. How-

ever, even if feature-based matching is applied here,

such an exhaustive matching procedure could be quite

costly. For this reason, matching is performed on only

a subset of the available reference images. At the next

capture, a different subset is selected. This strategy

allows keeping the processing rate sufﬁciently high

while giving access to a large quantity of reference

images. Obviously, it might take few captures before

a successful match is obtained, but with an adequate

frame rate, the response can remain acceptable.

Each putative matching between a video frame and

a reference image is then validated by checking if the

established match set is supported by a valid 2-view

geometry. In order to reduce the computational cost

of this operation, an accelerated random sampling

strategy is applied here. Eight feature matches are

randomly selected and the corresponding fundamen-

tal matrix is computed. The match between the two

images will be considered to be good, if a large num-

ber of individual matches supports this fundamental

matrix; that is if for a given match pair, one point

lies close to the epipolar line of the other point, as

computed by this matrix. To speed up this validation,

the test is performed using only 8 match pairs among

which 6 must support the geometry in order for the

match to be accepted. That simpliﬁed strategy does

not fully guarantees the validity of a match, but the

probability that a wrongly matched pair of images sur-

vives to this test is nevertheless very low. Once an im-

age match pair has been accepted, an additional ﬁlter-

REAL-TIME LABEL INSERTION IN LIVE VIDEO THROUGH ONLINE TRIFOCAL TENSOR ESTIMATION

437

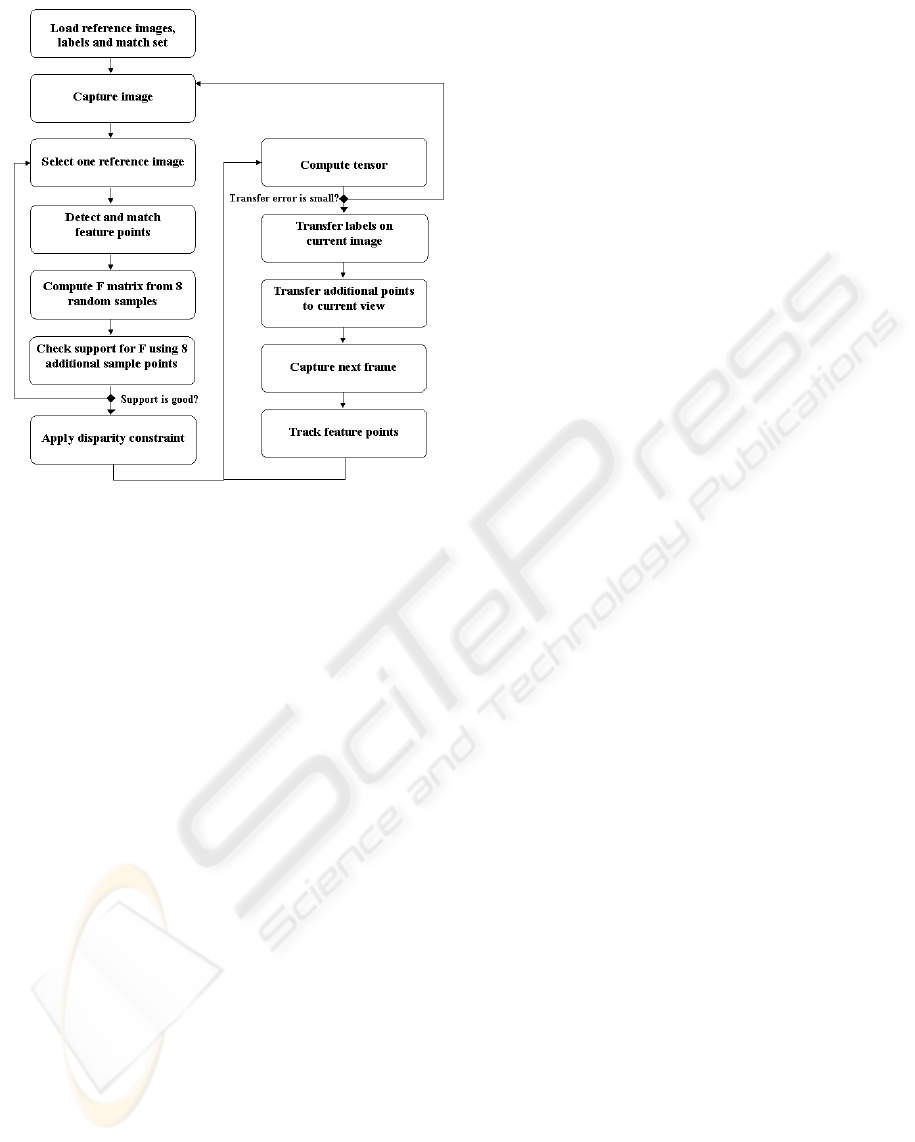
Figure 2: The virtual label insertion process.

ing step is applied on the proposed match set in order

to eliminate the obvious mismatches that remain. The

disparity constraint has proven to be quick and effec-

tive in performing this task (Vincent and Lagani

ere,

2001). It consists in eliminating any feature match

exhibiting a disparity vector that largely differs from

its neighbors. At this stage, a match is considered to

have been established between a reference image and

the currently seen image. This latter can now be sup-

plemented with the appropriate virtual labels; this is

done at the tracking phase.

5.2 The Tracking Phase

As mentioned previously, the transfer of the labels

from the reference image to the current is done using

the trifocal tensor. This is possible because each ref-

erence image is associated with two other reference

images, forming a triplet for which a rich match set is

available (as explained in Section 4). This means that

the image matching obtained is, in fact, a matching

between one image and the three images of a series of

reference images. It is therefore possible to compute

a tensor between a current frame and two of the im-

ages of the series. This tensor must however be com-

puted quickly in order to keep the frame rate high.

This computation must also be robust, as some false

matches are probably present in the match set found

during the matching phase. In addition, the estimated

tensor must have a good accuracy in order to pro-

duce well localized scene labels. For this reason, the

the tensor is estimated using an algebraic minimiza-

tion method and its accuracy is improved afterwards

through a quick outlier removal step. The details of

this online tensor estimation procedure are given in

the next section.

With an accurate tensor in hands, it is easy to trans-

fer the labels from the reference images to the current

view. The points that have been matched in this cur-

rent view are then tracked from frame to frame in or-

der to maintain the relation with the current series of

reference images. At each new camera position, the

tensor must be re-estimated with the match set that

includes the current frame points at their currently

tracked location. It is important to note that, when

points are tracked over time, more and more features

are unavoidably lost. If nothing is done, the tracked

set will eventually vanish. To overcome this prob-

lem, the match set is updated after each tensor esti-

mation. Indeed, using the pool of matches available

in the reference images, it is possible to transfer addi-

tional points on the image using that newly estimated

tensor. This last step ensures the long term viability

of the tracking phase.

6 ONLINE ESTIMATION OF THE

TENSOR

In this section we describe a method to quickly esti-

mate the trifocal tensor based on the use of two ref-

erence frames. This approach has been introduced in

(Li et al., 2004) for augmenting a scene in realtime

with virtual objects.

The trifocal tensor describes the projective geo-

metric relation of image triplets taken from cameras.

It can be conveniently estimated using the so-called

Algebraic Minimization method (Hartley and Zisser-

man, 2000). However, in the present application, two

problems have to be overcome: ﬁrst, the tensor es-

timation process must be fast; and second, the esti-

mated tensors must be accurate. This is to say that

we have to use all available matches when estimating

a tensor. Consequently, we have to counter the effect

of false matches introduced in the matching phase and

also, in the tracking phase. In fact, it is during this lat-

ter phase that outlier rejection is the most crucial. In-

deed, it is unavoidable that the tracker will lose some

features, and will introduce some wrong traces. This

is especially true in the case of sequences produced by

handheld cameras involving quick and saccadic mo-

tion. The estimation process therefore has to be ro-

bust to the presence of outliers. In order to solve this

problem, we developed an estimation scheme that ex-

ploits the geometrical properties of the problem and

that uses rapid robust estimation strategies.

One important properties of our system geometry

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

438

Figure 3: Average transfer error on the computed tensors in

a sequence of 1749 frames. Top: the tensors computed from

all putative triplets using AM; Middle: the improvements

achieved by using ﬁxed projection matrices; Bottom: the

resulting tensors reﬁned by applying the x84 rule.

resides in the fact that the tensors to be estimated are

always associated with two ﬁxed views (the reference

frames). Since the algebraic method uses parame-

trization of the projection matrices, we therefore have

two of the three projection matrices known which re-

duces the dimensionality of the problem. Our exper-

imentations have also shown that tensor estimation

subject to a ﬁxed projection matrices exhibit reliable

performance over long sequences. In addition, it has

the capability to attenuate the effect of false matches

and stabilizes the estimation results when only few

features are being tracked.

Each time a new tensor is computed using the al-

gebraic minimization approach, the average value of

the residual errors is then computed in order to as-

sess the quality of the resulting transfer. If its value

is smaller than a given threshold (we used 3 pixels),

then the tensor is judged to be of good quality and can

be used as is. Otherwise, additional steps to identify

and eliminate potential outliers are undertaken.

The strategy used to re-estimate the tensor depends

on the number of supporting triplets in the set of

points. When the proportion of supporting triplets is

high, this means that the quality of the tensor is not

good mainly because of the presence of a few strong

outliers. In this case, a statistical method based on the

so-called x84 rule (Fusiello et al., 1999) is used. Ab-

solute deviations of all triplets’ residual error are cal-

culated, from which a threshold is set as the 5.2 MAD

(Median Absolute Deviation). Points having larger

deviations are considered outliers and are eliminated.

In the opposite situation, i.e. when the number of

supporting triplets is relatively low, then the current

tensor is not able to guide the identiﬁcation of out-

liers. Cross-correlation has to be performed on each

Figure 4: Few frames of an online label insertion sequence

using the reference images of Figure 5.

putative triplet. All features on the current frame that

do not correlate well their potential correspondences

on both reference frames are rejected.

Once the outliers are rejected using one or the other

of these methods, the tensor has to be re-estimated

with all remaining triplets and its quality needs again

to be re-evaluated. The validity of the proposed es-

timation scheme is illustrated in Figure 3. The accu-

racy of the estimated tensor, in terms of transfer er-

ror (in pixels), has been evaluated for each frame of

a long sequence where the camera was freely moved

around the scene of interest. The ﬁrst graph is the

result of tensor estimation using only the Algebraic

method. The obtained errors illustrate well the neces-

sity of using additional steps to reﬁne the tensor esti-

mates. The second graph shows how the introduction

of the ﬁxed-projection-matrices constraint stabilizes

the results. Finally, the extra robust estimation steps

further improve the results by eliminating the remain-

ing outliers in the match set as shown in the bottom

graph.

7 RESULTS

Figures 4 to 7 presents few images showing re-

sults obtained when running our scene augmenta-

REAL-TIME LABEL INSERTION IN LIVE VIDEO THROUGH ONLINE TRIFOCAL TENSOR ESTIMATION

439

tion application. The system runs at approximately

14 frames/second on a regular P4 1.2GHz com-

puter equipped with a web cam with a resolution of

320x240.

The ﬁrst image of Figure 7 corresponds to the situ-

ation where a successful match has been obtained; in

this case, the camera frame has been matched to the

third reference image (shown in Figure 6). All the fea-

ture points that have been used to assess the validity

of this match are shown in light gray (the short lines

associated with each point correspond to the displace-

ment between the two matched images). These points

are also used to compute the tensor relation between

that current view and two reference images (here we

used reference images 1 and 2). Labels can then be

displayed and are pointing to the correct location by

virtue of the tensor transfer operation. The camera

is moved and new images are captured, the matched

point are tracked, the tensor is updated and the labels

are again transferred. Figure 7 shows other images

of the sequence in which the labels are indeed always

pointing at the right location.

In normal operation just the labels are shown and

not the feature points used for matching. This is

shown in Figure 4 and 5 where, this time, the 6 refer-

ence images of Figure 5 are used to annotate the video

sequence of Figure 4.

8 CONCLUSION

An augmented reality system has been presented

where a video sequence can be augmented with tex-

tual annotations. The augmentation is accomplished

by following a 2-step process. First, each incom-

ing frame of the captured video is matched with a

set of reference images. Currently a simple, but efﬁ-

cient, matching scheme is used where points are cor-

related by comparing their respective neighborhood.

The fact that each putative match is validated geomet-

rically eliminates most false matches. However, we

are currently investigating other matching strategies

that would make the matching process more robust to

perspective variation and changes in illumination.

The second step requires continuous estimation of

the trifocal tensor relation. The fact that we have in

hands a reliable set of matches associated to the refer-

ence images is key in this operation. Good tensor esti-

mates can therefore be quickly obtained using which

label transfer (from the reference views where they

have been inserted to the current view) becomes pos-

sible. By tracking the points over time, the tensor esti-

mate can be updated resulting in stable label insertion.

The main advantage associated with the use of pro-

jective entities (such as the tensor and the fundamen-

tal matrix) resides in the fact that no calibration in-

formation is required. The system can then easily

accommodate the use of different camera, as well

as zoom changes occurring during the augmentation

process. Neither 3D pose information nor metric in-

formation about the scene are required.

REFERENCES

Bell, B., Hollerer, T., and Feiner, S. (2002). An anno-

tated situation-awareness aid for augmented reality. In

Proc:UIST ACM Symp. on user interface sofware and

technology, pages 213–216.

Boufama, B. and Habed, A. (2005). Registration and track-

ing in the context of ar. ICGST Int. Journal on Graph-

ics Vision and Image Processing, V3.

Chia, K., Cheok, A., and Prince, S. (2002). Online 6 dof

augmented reality registration from natural features.

In Proc. International Symposium on Mixed and Aug-

mented Reality(ISMAR), pages 223–230.

Fusiello, A., Trucco, E., Tommasini, T., and Roberto, V.

(1999). Improving feature tracking with robust statis-

tics. Pattern Analysis and Applications, 2:312–320.

Hartley, R. and Zisserman, A. (2000). Multiple View Geom-

etry in Computer Vision. Cambridge University Press.

Kutulakos, K. and Vallino, J. (1998). Calibration-free aug-

mented reality. IEEE trans. on Visualization and Com-

puter Graphics, 4:1–20.

Li, J., Lagani

ere, R., and Roth, G. (2004). Online estima-

tion of trifocal tensors for augmenting live video. In

IEEE/ACM Symp. on Mixed and Augmented Reality,

pages 182–190.

Lourakis, M. and Argyos, A. (2004). Vision-based camera

motion recovery for augmented reality. In Computer

Graphics Int. Conference, pages 569–576.

Newman, J., Ingram, D., and Hopper, A. (2001). Aug-

mented reality in a wide area sentient environmemt.

In Int. Symp. on Augmented Reality, pages 77–86.

Roth, G. and Whitehead, A. (2000). Using projective vi-

sion to ﬁnd camera positions in an image sequence. In

Proc. of Vision Interface, pages 225–232.

Vacchetti, L., Lepetit, V., and Fua, P. (2004). Stable real-

time 3d tracking using online and ofﬂine information.

IEEE trans. on Pattern Analysis and Machine Intelli-

gence, 26:1385–1391.

Vincent, E. and Lagani

ere, R. (2001). Matching feature

points in stereo pairs: A comparative study of some

matching strategies. Machine Graphics and Vision,

10:237–259.

Vincent, E. and Lagani

ere, R. (2002). Matching feature

points for telerobotics. In IEEE Int. Workshop on Hap-

tic Virtual Env. and Applications, pages 13–18.

VISAPP 2006 - MOTION, TRACKING AND STEREO VISION

440

Figure 5: Annotation on the horse object. In order to accommodate changes in point of view, two series of reference images

are used here. The labels have been inserted in the ﬁrst image of each series, as shown here.

Figure 6: The three reference views and the set of matches.

Figure 7: An image is matched with the third reference image of Figure 3, making label insertion possible; label locations are

then correctly tracked over time.

REAL-TIME LABEL INSERTION IN LIVE VIDEO THROUGH ONLINE TRIFOCAL TENSOR ESTIMATION

441