USING DEFICITS OF CONVEXITY TO RECOGNIZE HAND

GESTURES FROM SILHOUETTES

Ed Lawson

Artiﬁcial Intelligence Center

Naval Research Laboratory

Washington, DC 20375

Zoran Duric

Department of Computer Science

George Mason University

Fairfax, VA 22030

Keywords:

convex hull, gesture recognition, human computer interaction, deﬁcits of convexity, k-means clustering.

Abstract:

We describe a method of recognizing hand gestures from hand silhouettes. Given the silhouette of a hand, we

compute its convex hull and extract the deﬁcits of convexity corresponding to the differences between the hull

and the silhouette. The deﬁcits of convexity are normalized by rotating them around the edges shared with the

hull. To learn a gesture, the deﬁcits from a number of examples are extracted and normalized. The deﬁcits

are grouped by similarity which is measured by the relative overlap using k-means clustering. Each cluster is

assigned a symbol and represented by a template. Gestures are represented by string of symbols corresponding

to the nearest neighbors of the deﬁcits. Distinct sequences of symbols corresponding to a given gesture are

stored in a dictionary. Given an unknown gesture, its deﬁcits of convexity are extracted and assigned the

corresponding sequence of symbols. This sequence is compared with the dictionary of known gestures and

assigned to the class to which the best matching string belongs. We used our method to design a gesture

interface to control a web browser. We tested our method on ﬁve different subjects and achieved a recognition

rate of 92% - 99%.

1 INTRODUCTION

Humans efﬁciently communicate using a wide range

of verbal and nonverbal communications mecha-

nisms. Traditional forms of human computer interac-

tion, however, provide only a limited range of inputs.

The mouse, for example, provides users with left

click, right click, and movement capabilities. Con-

trast this with hand gestures, a natural form of com-

munications, which has a virtually unlimited number

of instantiations. While the mouse and keyboard are

extremely popular and successful input devices, nat-

ural communications can make human computer in-

teraction more efﬁcient. In this paper, we describe a

novel method of static hand gesture recognition us-

ing convex hulls. Using this technique, we have built

a gesture interface to a web browser. We accurately

and efﬁciently recognize gestures captured with an in-

expensive web camera, despite a wide range of hand

orientations and locations. We also demonstrate the

ability to recognize multiple permutations of the same

gesture.

Given a hand silhouette, we compute the convex

hull and extract the deﬁcits of convexity, which cor-

respond to the difference between the hull and the sil-

houette of the hand. Deﬁcits of convexity are strongly

related to bitangents, the line tangent to a silhouette

at two distinct points. The bitangent, along with a

third point that is most distant from the bitangent is in-

variant under afﬁne transformations (Lamdan, 1988);

(Buesching, 1996). We train by extracting the deﬁcits

of convexity from all examples of each gesture. These

deﬁcits are clustered using k-means clustering. A rep-

resentative deﬁcit from each cluster is chosen and a

symbol is assigned to the deﬁcit. Gestures are rep-

resented by the string of symbols corresponding to

the nearest neighbor of each of the extracted deﬁcits.

Distinct sequences of symbols corresponding to the

training gestures are stored in a dictionary. Each of

the sequences stored in the dictionary correspond to

a different instantiation of a gesture. Given an un-

known gesture, its representation is created and com-

pared against the dictionary of known gestures. Ges-

tures are recognized if the corresponding sequence of

symbols is an exact match. If no matching sequence if

found, the gesture is rejected as an unknown gesture.

123

Lawson E. and Duric Z. (2006).

USING DEFICITS OF CONVEXITY TO RECOGNIZE HAND GESTURES FROM SILHOUETTES.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 123-128

DOI: 10.5220/0001376101230128

 SciTePress

The remainder of this paper is organized as follows.

Section 2 presents a discussion on related literature.

Section 3 outlines the methodology used to solve this

problem. Section 4 presents experimental results. Fi-

nally, section 5 presents conclusions and future work.

2 PREVIOUS WORK

One application of gesture recognition that has been

active for many years is sign language recognition.

Starner et al. shows a system that tracks sign lan-

guage in real time for continuous sentence recognition

(Starner, 1998). Their system takes measurements of

the hand (shape, orientation, and trajectory) and com-

bines these with hidden Markov models to produce

a powerful system capable of a recognition rate of

between 97.8 - 99.3 percent while using a wearable

computer.

Hand gestures have also been explored as a means

of human computer interaction. Oka et al. demon-

strates a system of hand gesture recognition and ﬁn-

ger tracking for use in an application called the En-

hanced Desktop (Oka, 2002). An image of the ap-

plication (such as a drawing application) is projected

onto a desk and users can then manipulated the image

using hand gestures. It is necessary to both directly

manipulate objects (by doing tasks such as grabbing

an object and moving it) and communicate with the

computer using symbolic gestures.

Hidden Markov Models (HMM) are a popular

method to use in the recognition of gestures (Starner,

1998). HMMs were originally employed in the ﬁeld

of automatic speech recognition (ASR). The dynamic

natures of both gesture and speech suggested that

a similar approach might be successful in gesture

recognition. Oka uses a HMM to recognize 12 differ-

ent gestures, based on the direction of motion of the

detected ﬁngertips (Oka, 2002). The authors boast

an accuracy rate of 99.2% of single ﬁnger gestures

and an accuracy rate of 97.5% of double-ﬁnger ges-

tures. Starner achieved similar recognition rates in

ASL recognition (Starner, 1998).

The major difﬁculty in using HMMs for gesture

recognition is related to the quality of the sensor.

When the sensor quality is poor, tracking becomes

much more difﬁcult. In such situations, measure-

ments become less reliable and HMMs yield poor re-

sults.

3 METHODOLOGY

A convex hull is a geometric shape such that no

two points in the shape are connected by a line seg-

ment that contains points outside of the shape (Oviatt,

2002). Fig. 1 shows two examples of convex hulls of

hand gestures. The lines show the convex hull while

hull points are marked with an x. The gesture on

the left is the gesture created by extending the index

ﬁnger and curling the remaining ﬁngers towards the

palm. The gesture on the right is the gesture created

by extending and splaying all of the ﬁngers.

Figure 1: Gesture Silhouette and Convex Hull.

We compute the convex hull using the graham scan

algorithm, which was selected for its speed and sim-

plicity. The graham scan algorithm builds the convex

hull by systematically examining all the shape points

to determine if they are inside of or outside of the cur-

rent shape. Points inside of the shape are discarded,

while points outside of the shape are added to the hull.

The algorithm runs in time linear to the number of

points in the object (O’Rourke, 1998). Next, we ex-

tract the deﬁcits of convexity. Starting at the top-left

hull point, we trace the contour of the hand until an-

other hull point is found. The contour of the hand can

be efﬁciently traced by examining points neighbor-

ing the current point (clockwise at the previous loca-

tion) until the next hand point has been found (Chang,

1989). The extracted deﬁcit of convexity is normal-

ized by rotating the edge shared with the convex hull

to align it with the X axis, shown in eq. (1). In this

equation, the start point indicates the starting convex

hull point and ﬁnish denotes the ﬁnished convex hull

point. The rotated deﬁcit is aligned by translating the

ﬁrst moment of the deﬁcit to the midpoint of the im-

age.

θ = − arctan(

finish

− y

start

finish

− x

start

) (1)

The process of computing the deﬁcits can occasion-

ally result in a deﬁcit that is extremely small. As we

see in ﬁg. 1, this is particularly true around the tips

of the ﬁngers and the side of the hand. Therefore,

we establish three thresholds for evaluating whether

a deﬁcit is accepted or rejected. The width thresh-

old T

rejects deﬁcits that are too narrow. The height

threshold T

rejects deﬁcits that are too short. The

area threshold T

rejects deﬁcits that meet the height

and width requirements, but are still too small. Ex-

amples of normalized deﬁcits of convexity that meet

these thresholds are shown in ﬁg. 2.

During training, a number of examples of each ges-

ture are captured. The deﬁcits of convexity from these

VISAPP 2006 - IMAGE UNDERSTANDING

124

Figure 2: Normalized Deﬁcits of Convexity extracted from

the Silhouette.

examples are extracted, normalized and clustered ac-

cording to their shape. The selection of the number of

clusters (k) is critical to the success of the methodol-

ogy. A value that is too low may not have the ability to

learn all of the instantiations of all of the gestures. A

value that is too high will memorize individual exam-

ples and will not have the ability to generalize. Sec-

tion 4 describes the selection of k as it relates to one

speciﬁc set of gestures.

Clustering requires a direct comparison of the

deﬁcits of convexity. While there are a number of

ways to accomplish this, we have developed a tech-

nique that provides a similarity score from 0 to 1. To

compare the deﬁcits, the number of pixels in the inter-

section of the two deﬁcits is computed and divided by

the number of pixels in the union of the two deﬁcits.

s =



∩ p



∪ p



(2)

A score of 1 indicates a perfect match, while a score

of 0 indicates that the deﬁcits have no pixels in com-

mon. This measure is similar to the L1 / city-block

distance normalized by the union of the two shapes.

K-means clustering computes a local maxima. A

better answer can be found by clustering a number of

times and evaluating the answers. The clustering is

evaluated by measuring the sum of the within group

variance (SSW) given by eq. (3) (Jain, 1991).

SSW =



j=1



i=1

−

)

(3)

The cluster mean (

) is the deﬁcit that is the most

similar to all of the deﬁcits in the cluster. Good

clustering results in a small within group variance.

K-means clustering terminates either when the SSW

is below a threshold or when a predeﬁned number

of iterations has been completed. Once completed,

the cluster templates and unique symbols to represent

each cluster are stored for later use.

When a gesture is presented during training mode,

the deﬁcits of convexity are extracted in a counter-

clockwise manner starting at the ﬁrst point encoun-

tered on the ﬁrst row when scanning from left to right.

Each deﬁcit extracted is normalized and compared to

each of the cluster templates. The resulting sequence

of symbols is stored in a dictionary during training

mode. During testing, the sequence of symbols is

compared to known sequences in the dictionary to

ﬁnd the matching gesture.

By only returning exact matches, we make the as-

sumption that we may not know every gesture pre-

sented (open set assumption). If every gesture pre-

sented will be from the database, we could return the

closest matching string or return the nearest N neigh-

bors of each cluster and use a voting scheme.

4 EXPERIMENTAL RESULTS

Using this technique, we built a system to control a

web browser using hand gestures. To do this, we

ﬁrst analyzed the functionality of the web browser

and identiﬁed six important functions of web brows-

ing. These functions are moving the cursor (”point”),

clicking on a link / button (”click”), returning to the

previously viewed page (”back”), returning to the

home page (”home”), scrolling up or down a page

(”scroll”), and ﬁnally stopping a page from loading

(”stop”). Next, a gesture is associated with each of

these functions. That is, when the gesture is recog-

nized the associated function is executed. The point

and scroll gestures use the relative difference between

the location of the gesture to determine the amount to

move the cursor or page (Lawson, 2005). The ges-

tures chosen to be associated with each of the func-

tions are shown in the table below. In the top row is

point, click; second row is home, back; third row is

stop, scroll.

Images are captured with an inexpensive web cam-

era (Creative Web Cam Pro Ex), pointed down on

the hand is it makes gestures against a solid colored

background. The hand is extracted by subtracting the

background based on some statistics gathered before-

hand.

The deﬁcits of convexity are captured, normalized

and compared against the thresholds established ear-

lier. For these experiments, the hand image size is

320x240. The thresholds used were T

=15, T

20, T

= 500.

Data was collected from 5 different subjects (3

male, 2 female). The subjects were told how to make

each of the 6 gestures, but encouraged to make them

in a way that felt comfortable. Data was collected for

1 minute per gesture, a total of 6 minutes per sub-

ject. During this period of time, subjects were asked

to move their hand to different positions and to pivot

their wrist so that their hand appeared in different an-

gles. Subjects were also instructed to experiment with

different instantiations from the gesture that felt com-

USING DEFICITS OF CONVEXITY TO RECOGNIZE HAND GESTURES FROM SILHOUETTES

125

Figure 3: Gestures used to control the web browser.

Figure 4: Examples of the point gestures made by one sub-

ject.

fortable to them. Figs. 4 - 9 shows examples of ges-

tures that were collected from one subject. The ex-

amples show a wide variation in the location and ori-

entation of the hand as well as a number of different

permutations of each gesture. The click and stop ges-

tures also show several examples where the hand is

partially out of the ﬁeld of view.

The ﬁrst experiment analyzes the impact of vary-

ing the number of clusters. To evaluate this impact

of varying the number of clusters, we select a sub-

ject from the data set and split the data into a training

/ validation set and a testing set. Next, 5-fold cross-

validation is done over the training / validation set, the

results of which are shown in the ﬁg. 10.

The ﬁgure shows a low overall recognition rate

when the number of clusters is low (5-10) increas-

ing to a maximum when k = 12 (94 % recognized),

then gradually falling again. When there are too few

clusters, there is too much generalization. This gen-

Figure 5: Examples of the click gestures made by one sub-

ject.

Figure 6: Examples of the home gestures made by one sub-

ject.

eralization results in an inability to represent all of

the gestures or all of the different instantiations of

each gesture. On the other hand, when there are too

many clusters, more memorization occurs, resulting

in a poor overall recognition rate. When selecting

the number of clusters we must take this into account

to select the smallest number of clusters that is just

“large enough ”. Furthermore, when an unknown ges-

ture is presented, each extracted deﬁcit must be com-

pared against each of the cluster templates. A smaller

number of clusters means less processing time. In

this case, we select k = 12 as the preferred number

of clusters, which results in an estimated error rate of

6%. Fig 11 shows the clusters found when k = 5 (left)

and k = 12 (right). When K = 5, the mean variance

between the deﬁcit and the cluster mean is 0.1156.

When k = 12, the mean variance between the deﬁcit

and the cluster mean is 0.0958.

Next, we test the methodology on each of the 5

individuals. For each subject, the ﬁrst step is to ex-

tract and cluster all of the deﬁcits from the training

gestures. String representations for each of the train-

ing gestures are generated and stored in the dictionary.

Fig. 11 shows an example of the results of k-means

VISAPP 2006 - IMAGE UNDERSTANDING

126

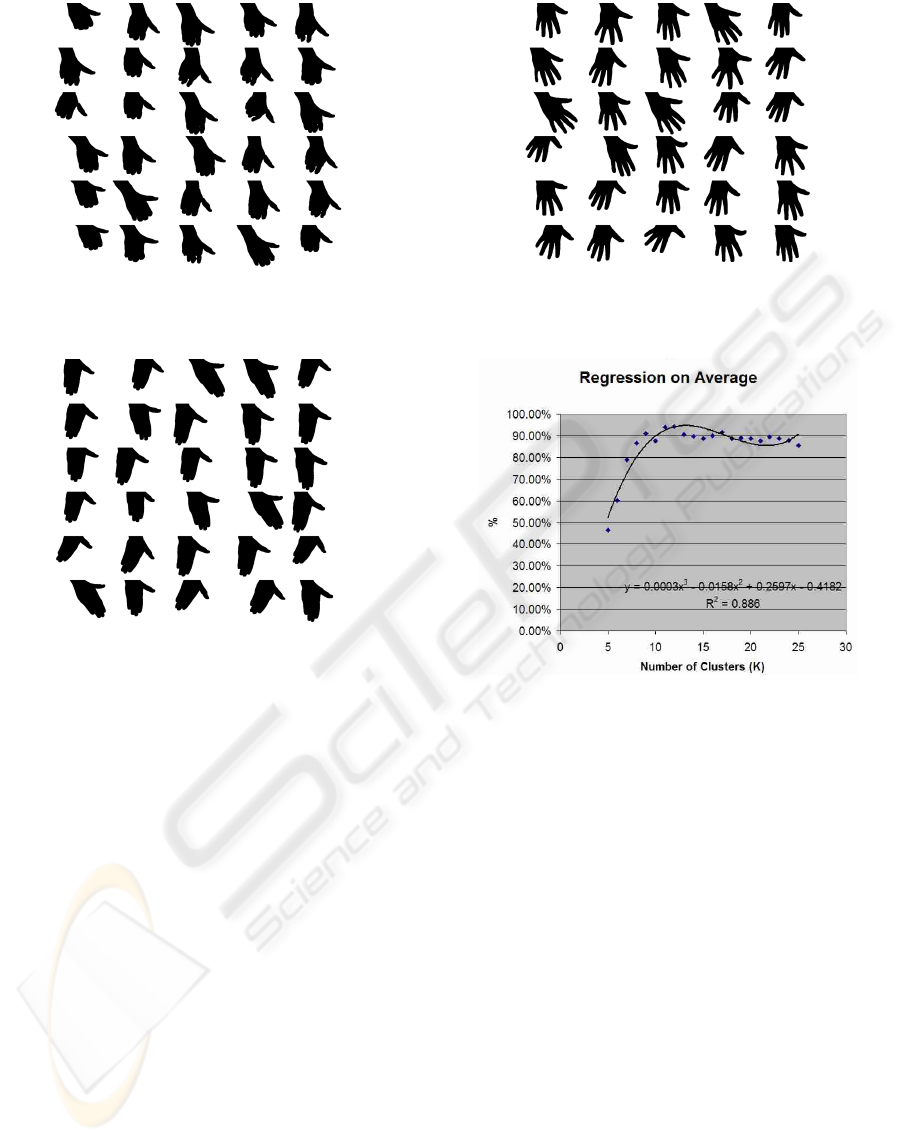
Figure 7: Examples of the back gestures made by one sub-

ject.

Figure 8: Examples of the scroll gestures made by one sub-

ject.

clustering when k=12 and some of the training ges-

tures and string representations stored in the dictio-

nary.

If we assign the letters a - l to deﬁcits 1 - 12, re-

spectively, the strings for the gestures in ﬁg. 12 are

“ce”(point), “de”(click), “h”(home), “d”(back), “cbji

(stop), and “c”(scroll).

When presented with an unknown gesture, the

deﬁcits of convexity are extracted and compared

against the cluster templates. A sequence of symbols

corresponding to the best matching cluster templates

is generated to represent the gesture. This sequence of

symbols is compared against the dictionary to ﬁnd the

matching string. The results of this process for each

of the 5 subjects is shown in the confusion matrices

below.

The average recognition rate for each subject

ranges from between 92.47% to 99.32%. Gestures are

recognized at a rate of between 92.93% to 97.36%.

The lowest recognition rate is for the stop gesture,

likely because this gesture contains the most deﬁcits

of convexity. The confusion matrices show only a

few instances of gestures being misclassiﬁed. Most

columns due not add up to 100%, due to the open set

Figure 9: Examples of the stop gestures made by one sub-

ject.

Figure 10: Evaluating the impact of the number of clusters

on the results.

assumption. This information is summarized in ﬁg.

14.

Analysis of variation (ANOVA) analyzes the inter-

action between the gesture and subject. In this case,

the null hypothesis is the recognition rate does not

vary between gesture and subject. At 95% conﬁ-

dence, the null hypothesis is accepted.

5 CONCLUSION

We have demonstrated an effective technique for

recognizing gestures captured by a noisy sensor. We

have demonstrated that it is possible to perform this

recognition with only a few clusters, and that there is

no signiﬁcant variation due to either different gestures

or different subjects. This technique can be applied to

recognize any gesture that has at least one deﬁcit of

convexity. A ﬁst, for example, has no deﬁcits of con-

vexity and would not be a good candidate for recog-

nition.

USING DEFICITS OF CONVEXITY TO RECOGNIZE HAND GESTURES FROM SILHOUETTES

127

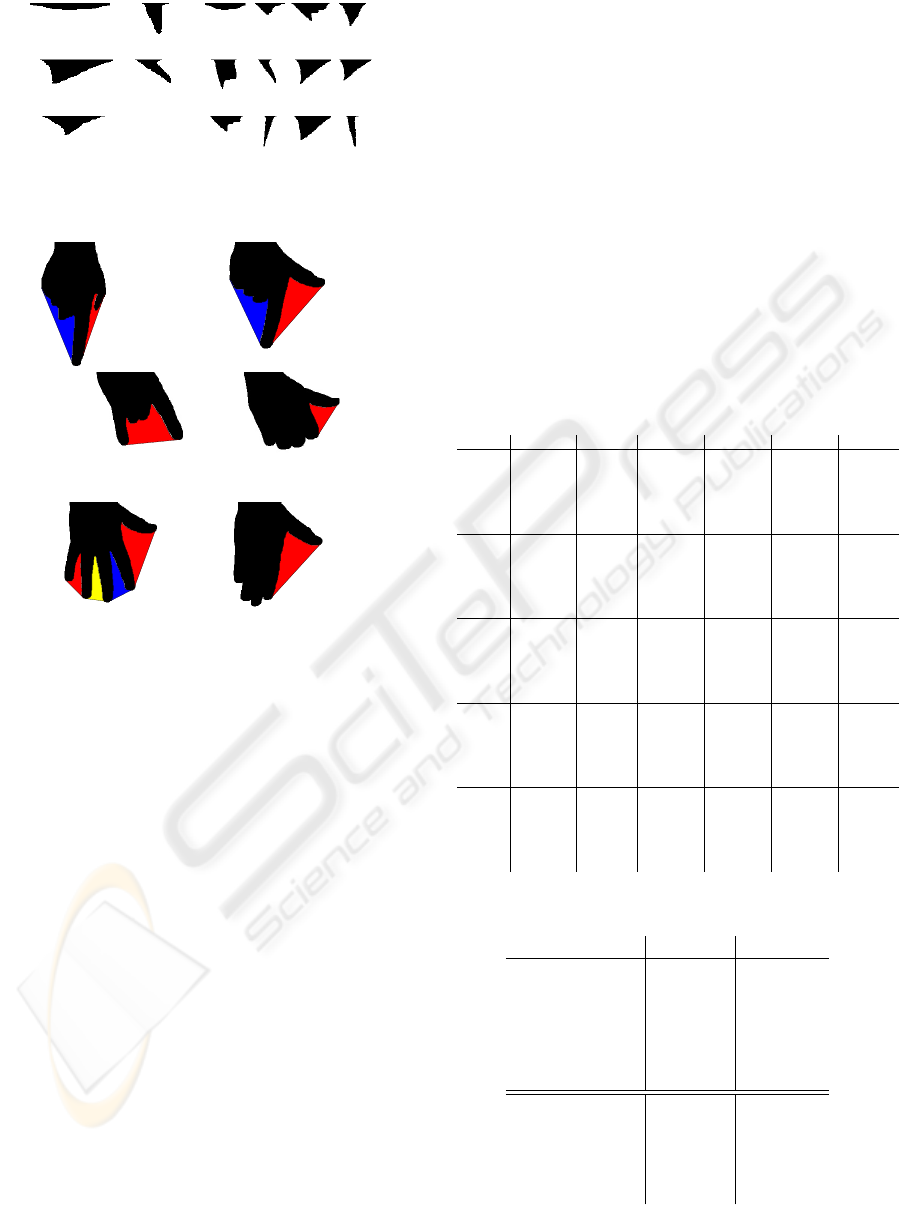
Figure 11: Cluster templates whenk=5(left) andk=12

(right).

Figure 12: Some of the training gestures with deﬁcits of

convexity highlighted.

Future efforts will focus on better ways of acquir-

ing examples and training. Ideally, we would like to

only acquire several examples of a gesture, then artiﬁ-

cially create additional examples. Furthermore, rather

than an ofﬂine learning mechanism, we would like to

learn on line. In this manner, the user can provide

only several examples, then begin to have gestures

recognized and gradually improve performance as the

system is used.

REFERENCES

Buesching, D. (1996). Efﬁciently ﬁnding bitangents. In

13th International Conference on Pattern Recogni-

tion.

Chang, S. (1989). Principles of Pictorial Information Sys-

tems Design. Prentice-Hall, New Jersey.

Jain, R. (1991). The Art of Computer Systems Performance

Analysis: Techniques for Experimental Design, Mea-

surement, Simulation and Modeling. John Wiley and

Sons, Inc.

Lamdan, Y. (1988). Object recognition by afﬁne invariant

matching. In Proc. CVPR 1988, pp. 335 - 344. IEEE.

Lawson, E. (2005). Designing and implementing a gesture

mouse. In HCII International 2005.

Oka, K. (2002). Real-time tracking of multiple ﬁngers and

gesture recognition for augmented desk interface sys-

tems. In Proceedings of the Fifth IEEE International

Conference on Automatic Face and Gesture Recogni-

tion. IEEE.

O’Rourke, J. (1998). Computational Geometry in C. Cam-

bridge University Press, Cambridge.

Oviatt, S. (2002). Designing the user interface for mul-

timodal speech and pen-based gesture applications:

State-of-the-art systems and future research direc-

tions. In Human-Computer Interaction in the New

Millennium. New York: ACM Press.

Starner, T. (1998). Real-time american sign language

recognition using desk and wearable computer based

video. In IEEE Transactions on Pattern Analysis and

Machine Intelligence, volume 20, pages 1371–1375.

IEEE.

Point Click Back Home Scroll Stop

Point 91.84% 6.12% 0.04% 0.68% 0.68% 0.00%

Click

0.68% 95.92% 0.00% 0.00% 0.00% 0.00%

Back

3.40% 0.00% 87.76% 1.08% 0.00% 0.00%

Home

0.00% 0.00% 0.00% 94.56% 0.00% 0.00%

Scroll

0.00% 0.00% 0.00% 0.00% 94.56% 0.00%

Stop

0.00% 0.00% 0.00% 0.00% 0.00% 97.28%

Point 97.85% 1.08% 0.04% 0.00% 0.00% 0.00%

Click

0.00% 94.62% 0.00% 0.00% 0.00% 0.00%

Back

0.00% 0.00% 94.62% 1.08% 0.00% 0.00%

Home

0.00% 0.00% 0.00% 92.47% 0.00% 0.00%

Scroll

0.00% 0.00% 0.00% 0.00% 96.77% 0.00%

Stop

0.00% 0.00% 0.00% 0.00% 0.00% 78.49%

Point 99.19% 0.00% 0.00% 0.00% 0.00% 0.00%

Click

0.00% 99.19% 0.00% 0.00% 0.00% 0.00%

Back

0.00% 0.00% 100.00% 0.00% 0.00% 0.00%

Home

0.00% 0.00% 0.00% 100.00% 0.00% 0.00%

Scroll

0.00% 0.00% 0.00% 0.00% 100.00% 0.00%

Stop

0.00% 0.00% 0.00% 0.00% 0.00% 97.56%

Point 96.43% 0.00% 0.00% 0.00% 0.00% 0.00%

Click

0.00% 96.43% 0.00% 0.00% 0.00% 0.00%

Back

0.00% 0.00% 98.81% 0.00% 0.00% 0.00%

Home

0.00% 0.00% 0.00% 95.24% 1.19% 0.00%

Scroll

0.00% 0.00% 0.00% 0.00% 97.62% 0.00%

Stop

0.00% 0.00% 0.00% 0.00% 0.00% 94.05%

Point 100.00% 0.00% 0.00% 0.00% 0.00% 0.00%

Click

0.00% 86.96% 0.00% 0.00% 0.00% 0.00%

Back

0.00% 0.00% 91.30% 0.00% 0.00% 0.00%

Home

0.00% 0.00% 0.00% 100.00% 0.00% 0.00%

Scroll

0.00% 0.00% 0.00% 0.00% 97.83% 0.00%

Stop

0.00% 0.00% 0.00% 0.00% 0.00% 95.65%

Figure 13: Confusion Matrices for each of the subjects.

Description Average Variance

Point Gesture 97.06% 0.10%

Click Gesture

94.62% 0.21%

Back Gesture

94.50% 0.26%

Home Gesture

96.45% 0.12%

Scroll Gesture

97.36% 0.04%

Stop Gesture

92.93% 0.66%

Subject 1 93.65% 0.12%

Subject 2

92.47% 0.50%

Subject 3

99.32% 0.01%

Subject 4

96.70% 0.02%

Subject 5

95.29% 0.27%

Figure 14: Statistics from confusion matrices.

VISAPP 2006 - IMAGE UNDERSTANDING

128