
PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES
USING A PSEUDOCOLOR FUZZY HOUGH TRANSFORM FOR
ARC DETECTION
Marta Penas, Manuel G. Penedo, Noelia Barreira
Dpt. Computer Science. Universidade da Coru
˜
na
Campus de Elvi
˜
na S/N. 15071, A Coru
˜
na. Spain
Mar
´
ıa Jos
´
e Carreira
Dpt. Electronics and Computer Science. Universidade de Santiago de Compostela
Campus Sur. 15782, Santiago de Compostela. Spain
Keywords:
Perceptual primitives, Gabor wavelets, growing cell structures, chromaticity diagram, Hough transform.
Abstract:
This paper describes a computational framework for extracting the low-level directional primitives present in
an image and organizing them into circular arcs. The system is divided into three stages: extraction of the
directional features through an efficient implementation of the Gabor wavelet decomposition, reduction of the
high dimensional Gabor results by means of growing cell structures and detection of the circular arcs by means
of a pseudo-color Fuzzy Hough Transform.
1 INTRODUCTION
The boundaries of objects in an image often lead
to oriented and localised changes in intensity called
edges. Edge, segment and arc detection are the first
steps in many image analysis applications and they
are of great importance as they constitute the basis
for higher level analysis. It has always been a fun-
damental problem in computer vision that the higher
level processing stages suffer due to either too little or
too much data from the lower levels of the processing.
Thus, the quality of data available for further analysis
is very critical.
This paper describes a framework for the extrac-
tion of the directional properties present in an image
through Gabor wavelet decomposition (Gabor, 1946)
and the detection of the circular arcs that approximate
these properties through a circle detector based on the
fuzzy Hough transform (Duda and Hart, 1972).
The Gabor wavelet decomposition framework pre-
sented here is a computationally expensive process,
but provides precise information about the image
pixel orientations and is independent of the image
type. Moreover, we have implemented (M. Penas and
Penedo, 2003a) an approximation to Gabor wavelets
that reduces the computational time and memory re-
quirements through the use of a Gabor decomposition
in the spatial domain, which is faster than conven-
tional frequency domain implementations.
A previous paper (M. Penas and Mari
˜
no, 2005) de-
scribes a line segment detector based in the combi-
nation of a pseudo-colour Hough transform and the
Burns segment detector. The fuzzy Hough transform
works properly in simple images that only contain the
objects to detect, but has some limitations in complex
images due to its global nature. Due to this limita-
tions, we have proposed a refinement of the pseudo-
colour Hough transform through the introduction of
some principles of the Burns segment detector.
This paper introduces the pseudo-colour fuzzy
Hough transform for the detection of circular arcs.
These circular arcs could be combined with the line
segments previously detected in a perceptual group-
ing framework that integrated the relationships of-
fered by the Gestalt psychology (parallelism, continu-
ity, similarity, symmetry, common region and closure)
among input tokens to form large groups that could be
useful for object detection or image classification.
2 EXTRACTION OF
DIRECTIONAL PRIMITIVES
This section contains a brief introduction of the first
stages of the process, the extraction of the direc-
tional primitives present in the image through Gabor
wavelet decomposition and the organisation of these
results through a growing cell structure. These stages
construct the pseudo-colour images that the circular
434
Penas M., G. Penedo M., Barreira N. and José Carreira M. (2006).
PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES USING A PSEUDOCOLOR FUZZY HOUGH TRANSFORM FOR ARC DETECTION.
In Proceedings of the First Inter national Conference on Computer Vision Theory and Applications, pages 434-439
DOI: 10.5220/0001363004340439
Copyright
c
SciTePress

arc detector will receive as input.
Gabor wavelets (Gabor, 1946) are complex expo-
nential signals modulated by Gaussians with two im-
portant properties that make them good edge detec-
tors: the optimisation of edge localisation (Deemter
and Buf, 2000) and the absence of image-dependent
parameter tuning. Their most important drawback
is their greedy demand for both memory and com-
putation time. In a previous paper (M. Penas and
Penedo, 2003b), we developed a more efficient, multi-
resolution spatial domain implementation of the Ga-
bor wavelet decomposition based on the convolution
of 11 1D-component masks obtained through the de-
composition of the 2D masks that define the wavelets.
This implementation uses the good edge localisation
property of Gabor wavelets, with the exact position of
an edge determined as a conjunction between a max-
imum in the modulus and a zero crossing in the even
or the odd part of the Gabor results.
In our Gabor decomposition, the input image is fil-
tered with a bank of 8 filters centred at frequency
1
4
and 8 orientations (
kπ
8
,k =0..7) leading to 8 re-
sulting images. A reduction of this output space di-
mensionality is necessary in the interest of efficiency.
Auto-organised structures are a suitable instrument to
achieve this dimensionality reduction as they allow
the reduction of the input space and the projection of
the topological order in the input space to the output
structure, simultaneously.
Figure 1: Left: Colourmap circle inside the RGB triangle.
Right: All orientations after the GCS analysis.
Self-organised maps, growing cell structures and
growing neural gas structures were investigated and
compared for their power of dimensionality reduc-
tion of Gabor decomposition results (M. Penas and
Penedo, 2001). Growing cell structures (GCS)
(Fritzke, 1994) provided significantly better results.
They are artificial neural networks based on self-
organised maps that eliminate the restrictions of the a
priori network size definition, incorporating a mech-
anism to add new processing elements when needed,
while maintaining the network topology.
To represent the different directionalities provided
by the auto-organised structure, each processing ele-
ment was assigned a colour from a colourmap to indi-
cate its orientation. The colourmap was obtained from
8 equidistant points on the perimeter of the maximum
circle inside the RGB triangle in the chromaticity di-
agram (Wyszecki and Stiles, 1982), centred at white
(see fig. 1-left). These 8 points represent the colours
assigned to the 8 main orientations considered. Points
in the perimeter of the circle show the colour gradua-
tion assigned to the processing elements in the GCS.
Fig.1 right shows the GCS output from a ring demon-
strating the colours of the entire direction space, i.e.
0 − 2π.
Fig. 2 shows the results from three input images
that contain multiple circular arcs. The first column
shows the original images and the second column the
results from GCS analysis.
Figure 2: Left: images ’bicycle’, ’face’ and ‘cells’. Right:
results of GCS analysis.
3 CIRCULAR ARC DETECTION
THROUGH THE HOUGH
TRANSFORM
The Hough transform is widely used in Computer Vi-
sion and Pattern Recognition for the detection of geo-
metrical shapes that can be defined through paramet-
ric equations. Traditional Hough transform imple-
mentations are based on the results obtained by clas-
sical edge detectors, like Canny or Sobel. This paper
describes the design and implementation of a fuzzy
Hough transform based on the pseudo-colour images
obtained from previous processes, this is, colour im-
ages where each colour represents an orientation.
PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES USING A PSEUDOCOLOR FUZZY HOUGH
TRANSFORM FOR ARC DETECTION
435
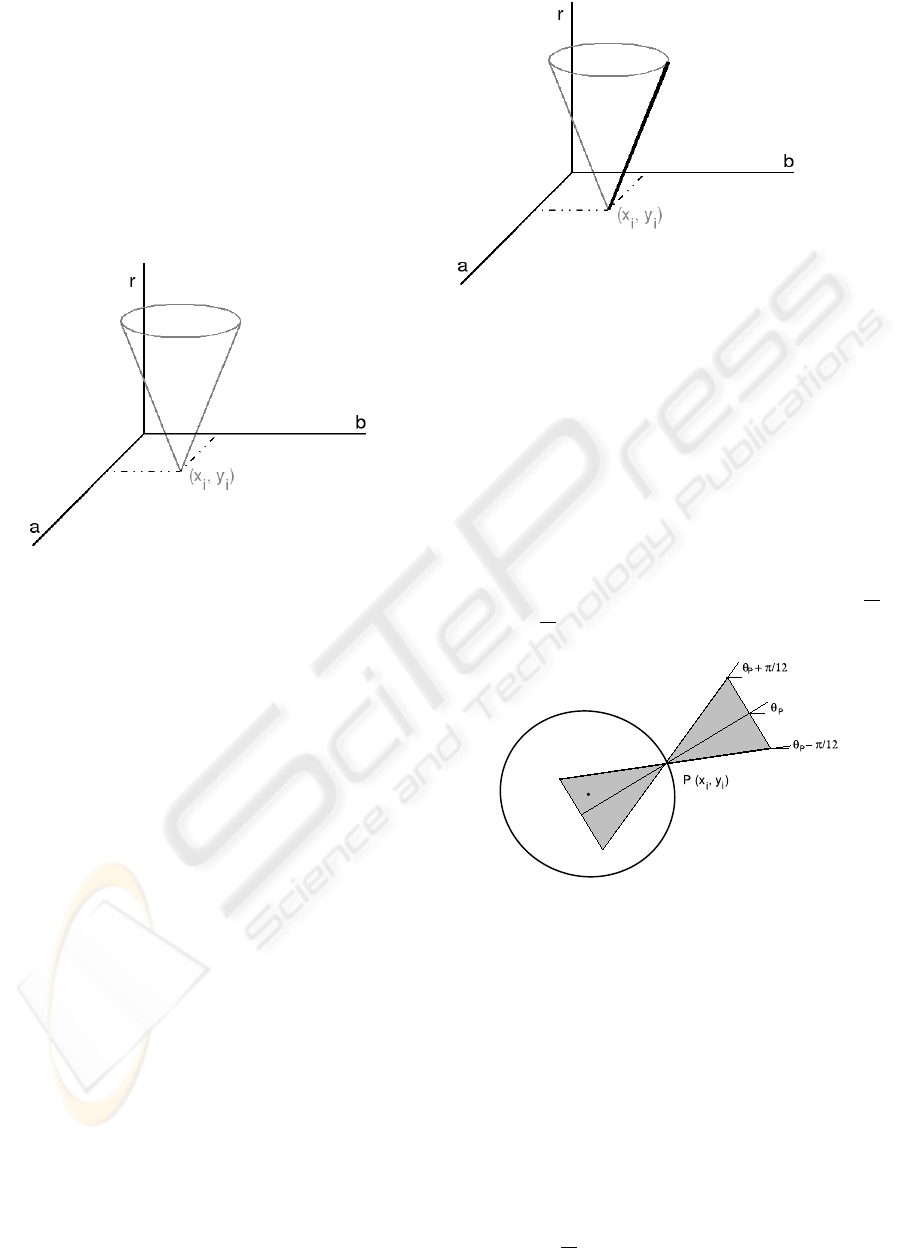
The Hough transform for circle detection is based
on the parametric equation of the circle, defined as:
(x
i
− a)
2
+(y
i
− b)
2
= r
2
(1)
where (a, b) are the coordinates of the circle centre
and r is the radius. The implementation of the Hough
transform in a digital computer requires the quantisa-
tion of the continuous a − b − r space into suitable
sized (a ×b ×r) cubes and the association of
each of these cubes with a cell of a 3D accumulator
array A of (N
a
× N
b
× N
r
) size.
Figure 3: 3D voting space of the standard Hough transform
for circle detection.
In the standard Hough transform, each edge pixel
(x
i
,y
i
) votes for all the possible circles that pass
through it. This voting process generates a 3D cone
as depicted in fig. 3. This approach needs to be en-
hanced to deal with the edges in our colour-labelled
images, where the colour of a pixel represents the ori-
entation of its normal line an determines where the
centre of the circle must be located. Therefore, the
voting space of a pixel (x
i
,y
i
) is reduced to the line
depicted in fig. 4. Thus, the use of the orientational
information highly reduces the computational com-
plexity of the process.
Due to the multiplicity of the edges in the pseudo-
colour images and the inaccuracies in the edge loca-
tion and orientation, we have implemented a fuzzy
Hough transform where each pixel votes, not only for
the orientation defined by its colour, but also for the
adjacent orientations.
3.1 Fuzzy Hough Transform for
Circle Detection
The process begins with the quantisation of the Hough
space into (N
a
× N
b
× N
r
) cells, where N
a
= I
x
,
N
b
= I
y
, N
r
= min(I
x
,I
y
) and (I
x
,I
y
) are the
dimensions of the input image. As previously men-
tioned, each cell is assigned to a position in a 3D ac-
cumulator array A. In this quantisation, a = b =
Figure 4: The line on the cone’s surface is the voting space
of the pseudo-colour Hough transform.
r =1in order to achieve the maximum precision
possible.
Then, the contribution of each pixel P =(x
i
,y
i
)
to the accumulator array is computed. First, the angle
θ
P
of the pixel is determined from its colour. Then,
the voting space of the pixel is constructed. In the
fuzzy Hough transform, each pixel votes for the set of
centres and the corresponding radios contained in the
grey area depicted in fig. 5. This area is delimited by
the two lines that pass through P with slopes θ
P
+
π
12
and θ
P
−
π
12
and by the maximum radius stipulated.
Figure 5: Voting space of pixel P in the pseudo-colour
fuzzy Hough transform for circle detection.
The contribution of the pixel P to the accumula-
tor array is not homogeneous for all the (a − b − r)
in fig. 5. It is maximum over the line that passes
through P with slope θ
P
and decrease with the ori-
entation difference. Specifically, the contribution is
defined through the following Gaussian function:
A(a
j
,b
j
,r
j
)=e
−β·d(θ
P
,θ
j
)
(2)
where the parameter that defines the decay of the
Gaussian function β is set to 10, as the contribution to
the accumulator array must rapidly decrease with the
orientation difference, falling to the minimum when
d(θ
P
,θ
j
)=
π
12
.
VISAPP 2006 - IMAGE ANALYSIS
436
Once the voting process has finished, the following
step is the detection of maxima. Each maximum de-
tected in the accumulator array corresponds to a cir-
cle in the image that can contain one or more arcs.
For each maximum over a predefined threshold, an in-
verse Hough transform takes place removing the con-
tributions to the accumulator array of the pixels be-
longing, not only to the circle detected, but also to
the concentric neighbouring ones. The detection of
arcs takes place simultaneously to the inverse Hough
transform. When a pixel is removed from the accu-
mulator array, its orthogonal projection to the circle it
belongs to is determined. Once all the pixels involved
have been analysed, the circle is sequentially searched
determining which pixels have been coloured and thus
belong to an arc.
Fig. 6 right shows the circle detection results over
the images depicted in fig. 6 left.
Figure 6: Left: input images. Right: results of the arc de-
tection process with the fuzzy Hough transform.
The implementation just described accurately de-
tects the centres and radius of the circles but has two
important drawbacks, the computational complexity
and the memory elapsed. Next section describes
a probabilistic implementation of the fuzzy Hough
transform that reduces the computational complexity
at the expense of reducing the quality of the results.
3.2 Probabilistic Fuzzy Hough
Transform for Circle Detection
The probabilistic Hough transform (Goulermas and
Liatsis, 1999) is based on the possibility of detecting
the circles in an image through the analysis of a lim-
ited subset of the edge points. It is also based in the
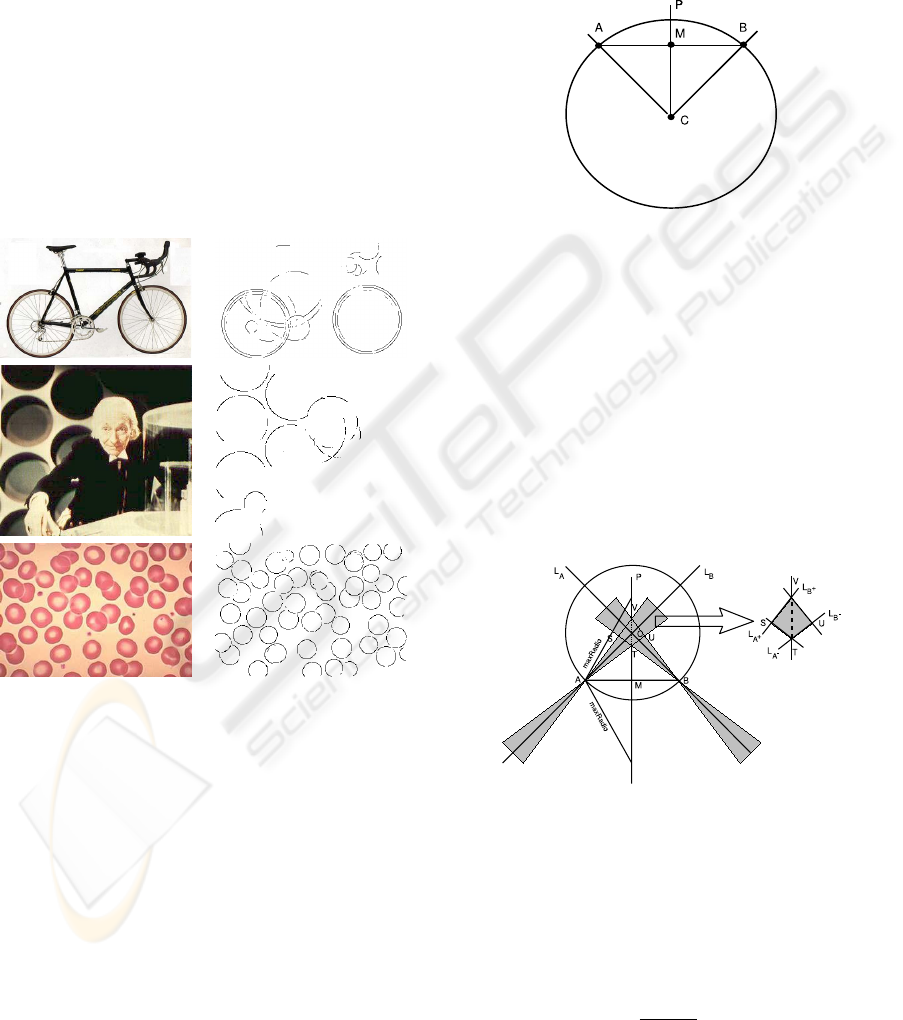
following property depicted in fig. 7: if A and B are
two points belonging to a circle, the normal lines that
connect them with the centre of the circle and the per-
pendicular bisector of the segment that joins them in-
tercept in the centre of the circle.
Figure 7: Property that relates two points that belong to a
circle.
Due to the innacuracies in the orientation estima-
tion and the effect of the discretization necessary in
the digital images, each point votes not only for the
radius and centre determined by the intersection of the
normals and the perpendicular bisector, but for those
in the voting space depicted in fig. 8. This voting
space consists of a line segment that belongs to the
perpendicular bisector and is delimited by the maxi-
mum radios allowed and/or the voting spaces of the
fuzzy Hough transform for circle detection in points
A and B, respectively.
Figure 8: Probabilistic fuzzy Hough transform. The voting
space is the dotted line segment enlarged on the right of the
figure.
The operation of the algorithm is divided into two
phases, the voting and the search for maxima in the
accumulator array. The voting begins with the ran-
dom selection and storage in a list L of a small per-
centage n (≈ 5% of N ) of the N edge points. Then,
for each of the K =
n·(n−1)
2
combinations of point
pairs, the voting space is computed and the correspon-
ding cells in the accumulator array are incremented.
PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES USING A PSEUDOCOLOR FUZZY HOUGH
TRANSFORM FOR ARC DETECTION
437

As in the fuzzy Hough transform, the contribution to
the accumulator array is not homogeneous and de-
pends on the orientation distance (see eq. 2).
Once the voting process has finished, the search
for maxima in the accumulator array begins. Each
maximum detected represents a candidate circle in the
image but, as only a small subset of points has voted,
in order to check the existence of the circle, the in-
verse Hough transform must calculate the percentage
of edge points that belong to the circle detected. Only
if this percentage is over a predefined threshold, the
candidate is considered a circle.
If the candidate is considered a circle, all the points
that belong to it are deleted from the edge image and
the accumulator array, the list L is updated up to its
original size n with points chosen at random and the
next maximum is analysed. If the circle is not valid,
a predefined number of points t (t ≈ 20% of n) are
erased and the same number of new points are in-
serted into L. The points erased are those that less
contributed to the accumulator array. The algorithm
stops when three non-valid circles are consecutively
detected.
Fig. 9 left shows the results obtained from the three
input images depicted fig. 9 right.
Figure 9: Left: input images. Right: results of the arc de-
tection process with the probabilistic Hough transform.
The probabilistic fuzzy Hough transform has
an important advantage with respect to the non-
probabilistic fuzzy Hough transform, the high com-
putational complexity reduction. But it also has some
important drawbacks. The first one is due to the use
of a small subset of points, which leads to inaccura-
cies in the results specially when the image contains
circles with very different sizes. Also, as the points
are randomly chosen, the results can vary among the
executions. Finally, the probabilistic Hough trans-
form works with combinations of pairs of points, if
the sample of points analysed has to be renewed many
times during the execution, the computational time
can exponentially grow.
In order to improve the results of the probabilis-
tic fuzzy Hough transform and to reduce the com-
putational complexity of the fuzzy Hough transform,
some basic principles from both implementations
have been combined in a new probabilistic fuzzy
Hough transform.
This implementation of the Hough transform is
very similar to the fuzzy Hough transform introduced
in sec. 3.1 but only a determined percentage N of
the input edge points is analysed. The sample points
are not randomly chosen, but homogeneously selected
from the input image. Empirically, we have checked
that a percentage of N ≥ 33% of the edge points pro-
duces good results.
The voting process of the sample points is analo-
gous to the one described in sec. 3.1 for the fuzzy
Hough transform. The voting process is followed by
the search for maxima in the accumulator array. As
in the probabilistic fuzzy Hough transform previously
described, each maximum detected represents a pos-
sible circle in the image but, as only a small subset
of points has voted, in order to check the existence of
a circle, the inverse Hough transform must compute
the percentage of edge points that belong to the circle
detected. Only if this percentage is over a predefined
threshold, the candidate is considered a circle.
Fig. 10 right shows the arc detection results from
the three input images depicted in fig. 10 left. These
results are very similar to those obtained by the fuzzy
Hough transform (fig. 6 right) while the computa-
tional complexity of this implementation is consider-
ably lower.
4 DISCUSSION AND
CONCLUSION
This paper describes a computational framework for
the detection of circular arcs in 2D digital images.
The framework is divided into three stages: the direc-
tional primitive extraction through Gabor wavelets,
the organisation of these primitives through auto-
organised structures and the circle detection through
a probabilistic fuzzy Hough transform.
The pseudo-colour fuzzy Hough transform intro-
duced in sec. 3.1 produces very good results, but it
has an important drawback, the high computational
complexity. The probabilistic Hough transform in-
troduced in sec. 3.2 overcomes this drawback but
VISAPP 2006 - IMAGE ANALYSIS
438

Figure 10: First column: input images. Second column: re-
sults of the arc detection process with the new probabilistic
Hough transform.
its results are not too accurate. Finally, the proba-
bilistic Hough transform introduced at the end of sec.
3.2 produces good results while keeping the compu-
tational complexity low, through the introduction of a
new way of selecting the candidate edges.
Fig. 11 shows the computational time (in minutes)
of the three versions of the Hough transform descri-
bed in this paper. The data depicted in fig. 11 have
been collected from the analysis of 10 input images
containing a different number of edge points rang-
ing from 4026 to 19227, and shows that the compu-
tational complexity depends both on the number and
the distribution of the edge points.
0 4026 5912 7613 7730 8435 10695 14450 14510 14922 19227
0
2,5
5
7,5
10
12,5
15
17,5
20
22,5
25
27,5
30
32,5
35
Fuzzy Hough
transform
Subsampled
probabilistic fuzzy
Hough transform
Probabilistic fuzzy
Hough transform
Number of edge points
Computational time (min)
Figure 11: Computational times of the alternative versions
of the fuzzy Hough transform.
The three implementations could be improved
through the use of directional information. The
pseudo-colour images that the fuzzy Hough transform
receives as input contain information about the orien-
tation of the edges, but not about their direction. The
directional information could be introduced through
the application of a Sobel filter to the pseudo-colour
edge images, where the noise presence is almost null.
The use of directional information could reduce the
computational complexity of the three implementa-
tions and increment the accuracy of the probabilistic
ones.
ACKNOWLEDGEMENTS
This paper has been partly supported by the Xunta de
Galicia through grant PGiDT03TIC10503PR.
REFERENCES
Deemter, J. V. and Buf, J. D. (2000). Simultaneous detec-
tion of lines and edges using compound Gabor filters.
Journal of Pattern Recognition and Artificial Intelli-
gence, 14(4):757–777.
Duda, R. and Hart, P. (1972). Use of the hough transform
to detect lines and curves in pictures. Comm. ACM,
15:11–15.
Fritzke, B. (1994). Growing cell structures - a self-
organizing network for unsupervised and supervised
learning. Neural Networks, 7(9):1441–1460.
Gabor, B. (1946). Theory of communication. Journal of the
Institute of Electronic Engineers, 36(93):429–457.
Goulermas, J. and Liatsis, P. (1999). Incorporating gradi-
ent estimations in a circle-finding probabilistic hough
transform. Pattern Analysis and Applications, 2:239–
250.
M. Penas, M. J. C. and Penedo, M. G. (2001). Auto-
organised structures for extraction of perceptual prim-
itives. Lect. Notes Comp. Science, 2085:628–636.
M. Penas, M. J. C. and Penedo, M. G. (2003a). Ga-
bor wavelets and auto-organised structures for direc-
tional primitive extraction. Lect. Notes Comp. Sci-
ence, 2652:722–732.
M. Penas, M. J. C. and Penedo, M. G. (2003b). Perceptual
organization of directional primitives using a pseudo-
color hough transform. Lect. Notes Comp. Science,
2749:893–898.
M. Penas, M. J. Carreira, M. P. and Mari
˜
no, C. (2005). Seg-
ment extraction using burns principles in a pseudo-
color fuzzy hough transform. Lecture Notes Comp.
Science, 3523:175–182.
Wyszecki, G. and Stiles, W. S. (1982). Color science,
concept and methods, quantitative data and formulae.
John Wiley & sons.
PERCEPTUAL ORGANIZATION OF DIRECTIONAL PRIMITIVES USING A PSEUDOCOLOR FUZZY HOUGH
TRANSFORM FOR ARC DETECTION
439
