
HUMAN BODY TRACKING BASED ON PROBABILITY
EVOLUTIONARY ALGORITHM
Shuhan Shen, Weirong Chen
School of Electrical Engineering, Southwest Jiaotong University, Chengdu, China
Keywords:
Tracking, Human Tracking, Probabilistic evolutionary algorithm.
Abstract: A novel evolutionary algorithm called Probability Evolutionary Algorithm (PEA), and a method based on
PEA for visual tracking of human body are presented. PEA is inspired by the Quantum computation and the
Quantum-inspired Evolutionary Algorithm, and it has a good balance between exploration and exploitation
with very fast computation speed. The individual in PEA is encoded by the probabilistic compound bit,
defined as the smallest unit of information, for the probabilistic representation. The observation step is used
in PEA to obtain the observed states of the individual, and the update operator is used to evolve the
individual. In the PEA based human tracking framework, tracking is considered to be a function
optimization problem, so the aim is to optimize the matching function between the model and the image
observation. Then PEA is used to optimize the matching function. Experiments on synthetic and real image
sequences of human motion demonstrate the effectiveness, significance and computation efficiency of the
proposed human tracking method.
1 INTRODUCTION
With the fast developments of computer science and
technology, visual analysis of human motion in
image sequences interests more and more
researchers from both laboratory and industry.
Human motion analysis has many potential
application areas such as intelligent visual
surveillance, advanced human-computer interface,
virtual reality, etc. Human tracking is a particularly
important issue in human motion analysis. How to
track human accurately and fast is a challenging task,
and it has been a popular topic in the research of
computer vision.
Tracking can be considered to be equivalent to
establishing coherent relations of image features
between frames with respect to position, velocity,
shape, texture, color, etc (Hu et al., 2004). Tracking
can be divided into region-based tracking
(Haritaoglu et al., 2000; Collins et al., 2000), feature
-based tracking (Breit et al., 2003), active-counter
-based tracking (Zhong et al., 2000; Paragio et al.,
2000), and model-based tracking. Model-based
tracking can provide abundant information of human
motion, but the increasing of subparts of the human
model would potentially incur high dimensionality
and make tracking a difficult task. To solve the
problem, many approaches have been investigated.
Gavrila et al. (Gavrila et al., 1996) split human
model into torso-head and limb partitions, and then
matching is implemented in the partitioned search
space. The Pfinder developed by Wren et al. (Wren
et al., 1997) employ a multi-class statistical model of
color and shape to obtain a 2D representation of
head and hands in a wide range of viewing
conditions. Isard et al. (Isard et al., 1998) propose
Condensation algorithm, which is a conditional
density propagation method for visual tracking.
Condensation is a useful approximate method for
nonlinearity and non-gaussianity posterior
probability within the Bayesian framework.
Condensation has various versions, and these
algorithms have been widely used now. Deutscher et
al. (Deutscher et al., 2001) present an Annealed
Particle Filtering (APF) method combined with
hierarchical search strategy and crossover operator.
Wu et al. (Wu et al., 2003) proposed a tracking
approach using mean field Monte Carlo (MFMC)
algorithm. In the approach, the subparts of human
model are considered to be independent and a set of
low dimensional particle filters interact with each
other to solve the high dimensional problem
collaboratively. Zhao et al. (Zhao et al., 2003)
303
Shen S. and Chen W. (2006).
HUMAN BODY TRACKING BASED ON PROBABILITY EVOLUTIONARY ALGORITHM.
In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 303-309
DOI: 10.5220/0001362603030309
Copyright
c
SciTePress

employ a 3D elliptical human model and segment
human body in crowed situations using Data-Driven
Markov Chain Monte Carlo (DDMCMC) algorithm.
In their further work (Zhao et al., 2004), Markov
chain Monte Carlo (MCMC) was used to tracking
segmented human in sequences.
Different from using particle filters within the
Bayesian framework, human tracking is considered
to be a function optimization problem in this paper,
so the aim is to optimize the matching function
between the model and the observation. Function
optimization is a typical application area of Genetic
Algorithms (GAs), but canonical genetic algorithms
is hard to be used here due to the high
dimensionality of human model and the requirement
of computation speed. In this paper, we present a
novel evolutionary algorithm called Probability
Evolutionary Algorithm (PEA) which is inspired by
the Quantum computation (Nielsen et al., 2000; Hey,
1996) and Quantum-inspired Evolutionary
Algorithm (QEA) (Han et al., 2002; Kim et al.,
2003), and then the PEA based human body tracking
is proposed in which PEA is used to optimize the
matching function. PEA has a good balance between
exploration and exploitation with very fast
computation speed, and it is suitable for human
tracking and other real-time optimization problems.
The rest of the paper is organized as follows.
Section 2 contains the Probabilistic Evolutionary
Algorithm (PEA). Section 3 describes the PEA
based human body tracking. Section 4 shows the
experimental results of our proposed tracking
algorithm. Finally, the conclusion follows in section
5.
2 PROBABILISTIC
EVOLUTIONARY ALGORITHM
Probabilistic Evolutionary Algorithm (PEA) is
inspired by the Quantum computation and the
Quantum-inspired Evolutionary Algorithm (QEA).
QEA is characterized by the representation of
quantum-bit, the observation step and the update
step with quantum gate. QEA performs well in the
function optimization and the knapsack problems.
For the full details of QEA, one can peruse Ref.
(Han et al., 2002; Kim et al., 2003). Considering that
QEA has only two observed states (0,1), it is more
suitable for the problem use binary coding than
multi-nary coding. Although multi quantum-bit can
be used to obtain multi observed states, this need to
use multi quantum gate which is extraordinarily hard
to design, and this shortcoming confines the
application area of QEA (Nielsen et al., 2000; Hey,
1996). To overcome the disadvantage, we present
the probability evolutionary algorithm (PEA).
2.1 The Individual’s Representation
in PEA
In PEA, the individual is encoded by the
probabilistic superposed bit, which is defined as the
smallest unit of information in PEA, as below.
Definition 1: A probabilistic superposed bit is a
vector that consists of the observation probabilities,
as:
1,
10
1
0
=+++
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
k
k
ppp
p
p
p
L
M
(1)
Where P
0
, P
1
, … P
k
give the probability that a
probabilistic superposed bit will be observed in the
‘0’ state, the ‘1’ state, …, and the ‘k’ state,
respectively. So a probabilistic superposed bit is a
linear superposition of the states 0 to k.
In PEA, an individual is defined as a string of the
probabilistic superposed bits. The individual is no
longer a deterministic state, but a linear
superposition of all kinds of states.
Definition 2: An individual p is a string of m
probabilistic superposed bits, as:
mjppp
ppp
ppp
ppp
j
k
jj
m
kkk
m
m
,,2,1,1,
10
21
1
2
1
1
1
0
2
0
1
0
KL
L
MMM
L
L
==+++
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=p
(2)
Where m is the length of the string. A PEA
individual can represent a linear superposition of
(k+1)
m
deterministic states probabilistically. For
example: for an individual with m=3 and k=9, the
probability to represent the state “123” is
p
1
1
×p
2
2
×p
3
3
, and the probability to represent the state
“709” is p
7
1
×p
0
2
×p
9
3
, etc. In the initialization of the
individual, all p
i
j
,i=0,1,…,k, j=1,2,…,m, are set to
1/(k+1), so the initial individual represents the linear
superposition of all possible states with the same
probability.
2.2 The Observation in PEA
The individual p in PEA can’t be used in the fitness
function directly, and an observation step should be
used to get the observed individual s. For p with
length m, it’s observed individual s=[s
1
,s
2
,…,s
m
],
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
304
where s
i
(i=0,1,…,m) is a deterministic k-nary value
and s is a deterministic k-nary string.
For the i-th probabilistic superposed bit [p
0
p
1
…p
k
]
T
in p, its observed value s
i
is obtained by the
following step. First, a random number r is
generated from the range [0,1]. Second, if P
0
+…+
P
v-1
<r< P
v
+…+ P
k
, s
i
is set to v.
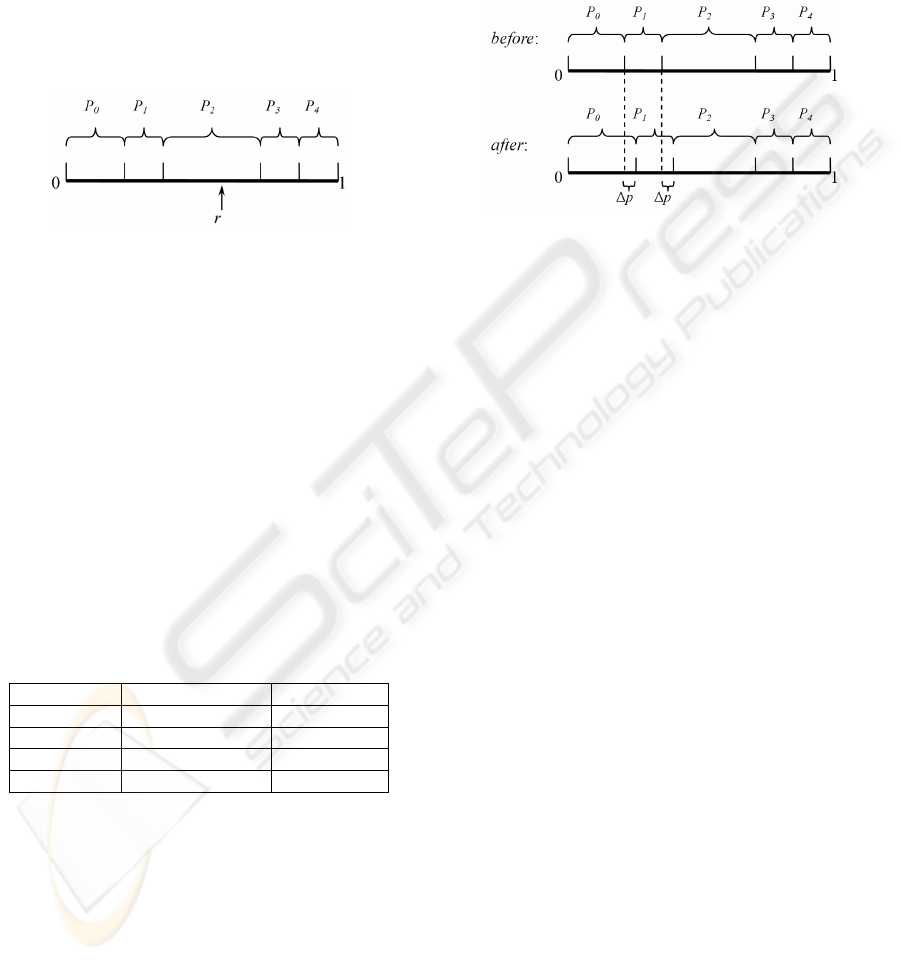
Figure 1 shows an example of the observation
step when k=4, r=0.6 and the i-th probabilistic
superposed bit in p is [0.25, 0.125, 0.375, 0.125,
0.125]
T
, here the observed value is s
i
= 2.
Figure 1: Observation.
2.3 The Update in PEA
The update operator is the only evolutionary
operator in PEA which can increase the observation
probabilities of some states, and decrease the
observation probabilities of some other states, in
order to make the high fitness state be observed
more likely.
Let s be the observed individual of p, and b be
the best solution of p at current generation. The
update value Δp of the i-th probabilistic superposed
bit [p
0
p
1
…p
k
]
T
in p can be formed from s and b, and
it can be found in Table 1.
s
i
=b
i
f(s)≥f(b) Δp
false false δ
true true 0
false true 0
true false 0
The update process is described in equation 3.
⎪
⎩
⎪
⎨
⎧
Δ+←
Δ−←
ppp
ppp
ii
ii
bb
ss
(3)
Considering that the observation probability can
not be negative, and to ensure the decreased
probability will not attenuate too fast, we make the
change value δ adaptively change according to the
decreased observation probability, as:
10, <<×= dpd
i
s
δ
(4)
Where d is the update rate that controls the
convergence speed of PEA. A bigger d leads a rapid
convergence speed but a rough search in the search
space, a smaller d has the opposite effect.
Figure 2 shows an example of the update step
when k=4, s
i
=2, b
i
=0 and Δp=0.05, here p
2
decrease,
p
0
increase, p
1
, p
3
and p
4
have no change.
Figure 2: Update.
2.4 The Procedure of PEA
The procedure of PEA is described in the following.
Begin
t←0
Initialization: Initialize population P(0)
Observation: Obtain the observed population S(0)
by observing P(0)
Evaluation: Calculate the fitness of the observed
individuals in S(0)
Store: Store S(0) into B(0)
While Termination-condition = false
t←t+1
Observation: Obtain the observed population S(t)
by observing P(t-1)
Evaluation: Calculate the fitness of the observed
individuals in S(t)
Update: Obtain the population P(t) by update
P(t-1)
Store: Store the best solution among B(t -1) and
S(t) into B(t), Store the best solution in B(t)
into gb
If Migration-condition = true
Migrate individuals in B(t) Locally or globally
End If
End While
End Begin
P(t) is the population, P(t)={p
1
t
,p
2
t
,…, p
n
t
}. p
j
t
is
the j-th individual at the t-th generation, where n is
the population size. In the initial population P(0), all
possible states in the search space should be
observed with the same probability.
Table 1: Lookup table of Δp, where f(·) is the fitness
function, s
i
and b
i
are the i-th bits of s and b,
ti l
HUMAN BODY TRACKING BASED ON PROBABILITY EVOLUTIONARY ALGORITHM
305
S(t) is the observed population,
S(t)={s
1
t
,s
2
t
,…,s
n
t
}. s
j
t
is the observed individual of
p
j
t
, and it is obtained by the observation step
described in section 2.2.
B(t) is the best solution population, B(t)=
{b
1
t
,b
2
t
,…,b
n
t
}. b
j
t
is the best solution of p
j
t
at the
t-th generation. gb is the global best solution. When
the local migration condition is satisfied, the best
solution among some of the solutions in B(t) is
migrated to them. When the global migration
condition is satisfied, the global best solution gb is
migrated to B(t).
Update operator generates the update position
and update value according to s
j
t
and b
j
t
, and evolves
p
j
t-1
to p
j
t
by the update step described in section 2.3.
3 PEA BASED HUMAN BODY
TRACKING
3.1 The Framework of PEA Based
Tracking
Different from tracking human using particle filters
within the Bayesian framework, tracking is
considered to be a function optimization problem in
this paper. We denote the human model by X, and
denote the observation associate with X by Z. The
function f(X,Z) represents the matching degree
between X and Z. Assume that we have known that
the model at time instance t-1 is X
t-1
, so the model X
t
at time instance t can be get by equation 5.
X
t
=X
t-1
+ΔX (5)
Here, ΔX is the change of the model X
t-1
. After
we get X
t
, the matching function f(X
t
,Z
t
) can be
calculated. Since X
t
is associated with ΔX, the
matching function can be written as:
f(X
t
,Z
t
) = g (ΔX) (6)
So tracking at time instance t is to optimize g
(ΔX) in ΔX’s search space. Generally, g (ΔX) is a
multi-modal function with many local best solutions,
and conventional optimization methods are difficult
to get the global best solution, so we use PEA to
optimize g (ΔX).
3.2 Search Strategy
Human model always has high dimensionality, and
search space partition is a useful strategy to change
the high dimensional problem into some low
dimensional problems and improve the matching
results (Gavrila et al., 1996; Deutscher et al., 2001;
Chen et al., 2005). Here we split the human model
into five partitions including the trunk-head partition
and four limb partitions. First, PEA is used to match
the trunk-head partition. Then, keeping the best
matched parameters of the trunk-head partition
constant, and PEA is used to math the four limb
partitions respectively.
In PEA based tracking, the model for the
previous frame only gives the initial position for the
current frame, so even if there are some matching
errors at the previous frame, the matching is easy to
be recovered in the following frames as long as the
search space of ΔX is enough.
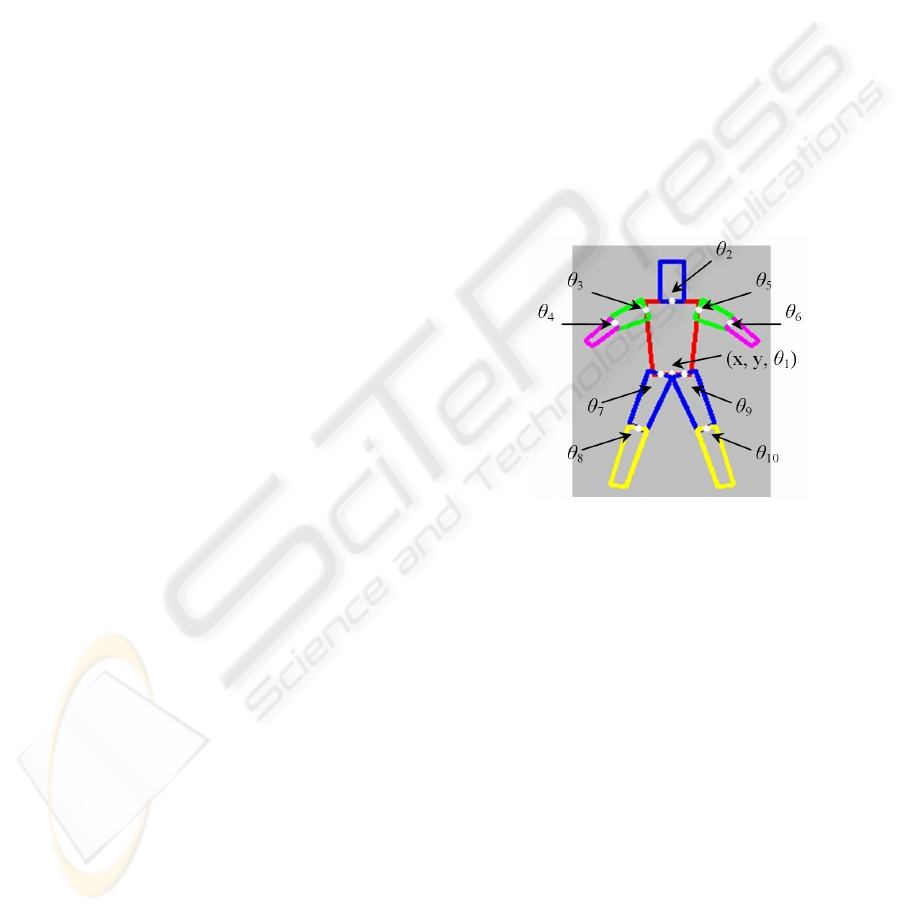
3.3 Human Model
We employ a 10-part articulated human body model
which consists of 10 parts and each pairs of neighbor
parts are connected by the joint point, as shown in
Figure3.
Figure 3: 2D human body model.
The model has 10 joints, and the root joint is at
the middle bottom of the trunk. The root joint has 3
degrees, and each of the other 9 joints has 1 degree.
The model X can be written as:
X = {x, y, θ
1
, θ
2
, …θ
10
} (7)
Here, x and y represent the location of the root
joint, and θ
1
,θ
2
…θ
10
represent the swiveling angles
of the 10 joints. ΔX can be written as:
ΔX={Δx, Δy, Δθ
1
, …Δθ
10
} (8)
Human motion is a gradually changed movement,
so ΔX can be limited in a logical small scope. This
scope can be learned or man-made. For example, Δx
and Δy are in the range [-19,19] (integral pixel),
θ
1
,θ
2
…θ
10
are in the range [-29,29] (integral degree).
Apparently, ΔX is suitable for decimal encoding
here, so the initial PEA individual of the trunk-head
partition and that of the limb partitions are shown in
Figure 4 and Figure 5 respectively.
In the observation step, the probabilistic
superposed bits corresponding with Δx and Δy can
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
306

be observed as {0,1,…39}, and subtracting 20
from these values give the true values of Δx and Δy.
The probabilistic superposed bits corresponding with
θ
1
,θ
2
…θ
10
can be observed as {0,1,…59}, and
subtracting 30 from these values give the true values
of θ
1
,θ
2
…θ
10
.
Figure 4: Initial PEA individual of the trunk-head
partition.
Figure 5: Initial PEA individual of the limb partition.
Here, we have a comparison of PEA with QEA.
If we use QEA here, ΔX should be encoded in
binary. For the same range of ΔX mentioned above,
the lengths of QEA’s individuals for trunk-head
partition and limb partitions are 24 and 12
respectively, and those lengths of PEA’s individual
are 8 and 4 respectively. In PEA and QEA, the most
intensive computation is the observation and the
update for each bit in the individual, so the shorter
length of individual make PEA run much faster than
QEA.
4 EXPERIMENTAL RESULTS
Two image sequences are used here to demonstrate
the effectiveness of PEA. Sequence 1 is a synthetic
image sequence generated by Pose software which
consists of 100 frames. Sequences 2 is a real image
sequence which consists of 325 frames. The
observation Z is also an important factor in tracking.
Here we use two types of visual cues: edge and
intensity. We compared the tracking results from
PEA with Annealed Particle Filtering (APF). All the
algorithms run on a 2.4GHz PC without code
optimization.
4.1 Parameters Setting
In APF based tracking, 200 particles are used, and
the particles are annealed for 8 times.
In PEA based tracking, we test two population
sizes. The population sizes of PEA1 and PEA2 are
set to 1 and 4, respectively. In PEA2, the local
migration occurs every generation between each pair
of neighboring individuals, and the global migration
occurs every 100 generations. The maximum
number of generations is 200.
4.2 Results
Some tracking results of PEA and APF for sequence
1 and sequence 2 are shown in Figure 6 and Figure 7
respectively. The average computation time for one
frame of PEA and APF are shown in table 2.
Algorithm
Particles or
Population size
second/frame
APF 200 3.77s
PEA2 4 1.62s
PEA1 1 0.41s
The results show that the PEA based tracking
algorithm yields more stable results than APF, and
run much faster than APF.
In some frames, PEA1 has some matching errors,
this is because there is only one individual in the
population and the premature convergence is
happened sometimes. PEA2 generates very stable
results in all the experiments.
In the experiments we also found that, when the
population size is bigger than 10, the tracking result
can not be improved further, so we suggest that the
population size is set to 2 to 8 in applications in
order to get a balance between the tracking accuracy
and the computation time.
Table 2: Avera
g
e com
p
utation time for one frame.
HUMAN BODY TRACKING BASED ON PROBABILITY EVOLUTIONARY ALGORITHM
307

5 CONCLUSIONS AND FURTHER
WORK
Model-based human tracking is a challenging
problem, since the human model has high
dimensionality. Different from tracking human using
particle filters, we consider tracking to be a function
optimization problem, and a novel evolutionary
algorithm called Probabilistic Evolutionary
Algorithm (PEA) is proposed to optimize the
matching function between the model and the
observation. PEA has a good balance between
exploration and exploitation with very fast
computation speed. Experiments on synthetic and
real image sequences of human motion demonstrate
the effectiveness, significance and computation
efficiency of the PEA based human body tracking
algorithm.
This paper mainly concerned to 2D tracking, but
the PEA based tracking method is easy to be
extended to 3D tracking, and our further work is to
extend our algorithm to 3D and combine more
observed cues such as motion and color. Our further
work also includes the further improving of the
searching ability and the computation speed of PEA.
REFERENCES
Breit, H. and Rigoll, G., 2003. A flexible mulitimodel
object tracking system. In Proceedings of International
Conference on Image Processing.
Chen, R., Liu, G.Y., Zhao, G.Y., et al, 2005. 3D human
motion tracking based on sequential monte carlo
method. Journal of Computer-aided Design &
Computer Graphics, vol. 17, no. 1, pp. 85-92.
Collins, R.T., Lipton, A.J., Kanade, T., et al, 2000. A
system for video surveillance and monitoring.
Carnegie Mellon Univ., Pittsburgh, PA, Tech. Rep.,
CMU-RI-TR- 00-12.
Deutscher, J., Davidson, A. and Reid, I., 2001. Articulated
partitioning of high dimensional search spaces
associated with articulated body motion capture. In
IEEE Proceedings of International Conference on
Computer Vision and Pattern Recognition, Hawaii.
Gavrila, D. and Davis, L., 1996. 3D model based tracking
of humans inaction: A multiview approach. In IEEE
Proceedings of International Conference on Computer
Vision and Pattern Recognition, San Francisco,
California.
Han, K.H. and Kim, J.H., 2002. Quantum-Inspired
Evolutionary Algorithm for a Class of Combinatorial
Optimization. IEEE Trans. on Evolutionary
Computing, vol. 6, no. 6, pp. 580-593.
Haritaoglu, I., Harwood, D., and Davis, L.S., 2000. W
4
:
real-time survei llance of people and their activities.
IEEE Trans. on Pattern Analysis Machine Intelligence,
vol. 22, no. 8, pp. 809-830.
Hey, T., 1996. Quantum computing: An introduction.
Computing & Control Engineering Journal, vol. 10, no.
3, pp. 105-121.
Hu, W.M, Tan, T.N, Wang, L., and Maybank, S.J., 2004.
A survey on visual surveillance of object motion and
behaviors. IEEE Trans. on System Man and
Cybernetics, vol. 34, no. 3, pp. 334-351.
Isard, M. and Blake, A., 1998.
CONDENSATION-conditional density propagation
for visual tracking. vol. 29, no. 1, pp. 5-28,
International Journal of Computer Vision.
Kim, K.H., Hwang, J.Y., Han, K.H., et al, 2003. A
Quantum-Inspired Evolutionary Algorithm for disk
allocation method. IEICE Trans. on Information &
Systems, vol. 86, no. 3, pp. 645-649.
Nielsen, M.A. and Chuang, I.L., 2000. Quantum
Computation and Quantum Information, Cambridge
University Press. Cambridge.
Paragio, N. and Deriche, R., 2000. Geodesic active
contours and level sets for the detection and tracking
of moving objects. IEEE Trans. on Pattern Analysis
and Machine Intelligence, vol. 22, no. 3, pp. 266-280.
Wren, C., Azarbayejani, A., Darrell, T. and Pentland, A.P.,
1997. Pfinder: Real-Time Tracking of the Human
Body. IEEE Trans. on Pattern Analysis and Machine
Intelligence, vol. 19, no. 7, pp.780-785.
Wu, Y., Hua, G. and Yu, T., 2003. Tracking Articulated
Body by Dynamic Markov Network. In Proceedings
of the Ninth IEEE International Conference on
Computer Vision.
Zhao, T. and Nevatia, R., 2003. Bayesian Human
Segmentation in Crowded Situations. In IEEE
Proceedings of International Conference on Computer
Vision and Pattern Recognition.
Zhao, T. and Nevatia, R., 2004. Tracking Multiple
Humans in Crowded Environment. In IEEE
Proceedings of International Conference on Computer
Vision and Pattern Recognition.
Zhong, Y., Jain, A., and Dubuisson, J.M., 2000. Object
tracking using deformable templates. IEEE Trans. on
Pattern Analysis and Machine Intelligence, vol. 22, no.
5, pp. 544-549.
VISAPP 2006 - MOTION, TRACKING AND STEREO VISION
308

(a)
(b)
(c)
Figure 6: Some tracking results of sequence 1. (a) Tracking based on APF. (b) Tracking based on PEA with population size
1 (PEA1). (c) Tracking based on PEA with population size 4 (PEA2).
(a)
(b)
(c)
Figure 7: Some tracking results of sequence 2. (a) Tracking based on APF. (b) Tracking based on PEA with population size
1 (PEA1). (c) Tracking based on PEA with population size 4 (PEA2).
HUMAN BODY TRACKING BASED ON PROBABILITY EVOLUTIONARY ALGORITHM
309
