SPEEDING UP SNAKES

Enrico Kienel, Marek Van

co and Guido Brunnett

Chemnitz University of Technology

Strae der Nationen 62, D-09107 Chemnitz, Germany

Keywords:

Active Contour Models, Snakes, Image Segmentation.

Abstract:

In this paper we summarize new and existing approaches for the semiautomatic image segmentation based

on active contour models. In order to replace the manual segmentation of images of the medical research of

the Center of Anatomy at the Georg August University of G

ottingen we developed a user interface based on

snakes. Due to the huge images (sometimes bigger than 100 megapixels) the research deals with, an efﬁcient

implementation is essential.

We use a multiresolution model to achieve a fast convergence in coarse scales. The subdivision of an active

contour into multiple segments and their treatment as open snakes allows us to exclude those parts of the

contour from the calculation, which have already aligned with the desired curve. In addition, the band structure

of the iteration matrices can be used to set up a linear algorithm for the computation of one single deformation

step. Finally, we gained an acceleration of the initial computation of the Edge Map and the Gradient Vector

Flow by the use of contemporary CPU architectures.

Furthermore, the storage of huge images next to additional data structures, such as the Gradient Vector Flow,

requires lots of memory. We show a possibility to save memory by a lossy scaling of the traditional potential

image forces.

1 INTRODUCTION

Imaging techniques have achieved a great importance

in many scientiﬁc domains, particularly in the med-

ical science. Whole series of digital photos are con-

sulted for the analysis of three-dimensional structures.

In order to reconstruct these three-dimensional mod-

els, it is necessary to perform an image segmentation.

In the framework of studying cellular events in the

embryonic development at the Georg August Univer-

sity of G

ottingen, the segmentation of huge images

of serial histological sections is done manually in a

tedious process. We developed a user interface that

allows a semiautomatic segmentation of these images

based on active contours.

The snake model, ﬁrst introduced by Kass (Kass

et al., 1987), offers a practical tool for the semiauto-

matic image segmentation. It combines many advan-

tages but features also some drawbacks which gave

reason for the publication of serveral improvements.

One major disadvantage is the necessity of initial-

izing a contour nearby the object’s edges due to the

narrow attraction range of the classical image en-

ergy. Kass proposed a convolution of the image with

a Gaussian kernel which slightly increases the cap-

ture range by blurring the original image. Rueck-

ert’s (Rueckert and Burger, 1996) multiscale approach

faces that problem by using different scales of the ker-

nel’s standard deviation. A balloon model was pro-

posed by Cohen (Cohen, 1991). Pressure forces along

the contour’s normals allow the inﬂation or the accel-

erated deﬂation of the snake. In order to increase the

attraction range of image edges Xu and Prince (Xu

and Prince, 1997) introduced an alternative image en-

ergy called Gradient Vector Flow. They calculate a

diffusion of the gradient vectors of a gray-level Edge

Map which additionally enables the active contour to

move into concave boundary regions. This is another

problem associated with the classical snake model.

The snake’s tendency of shrinking due to the for-

mulation of the internal energy terms discouraging the

stretching and bending behavior is sometimes stated

as a disadvantage, too. By applying Cohen’s balloon

model (Cohen, 1991) a snake is able to counteract the

contraction. Perrin (Perrin and Smith, 2001) proposed

alternative formulations of the internal energy which

323

Kienel E., Van

co M. and Brunnett G. (2006).

SPEEDING UP SNAKES.

In Proceedings of the First International Conference on Computer Vision Theory and Applications, pages 323-330

DOI: 10.5220/0001362403230330

 SciTePress

also produce locally smooth curvatures and an evenly

spacing of the control points. In contrast to the tra-

ditional method this approach avoids shrinking and

pushing the model toward a straight line.

In (Mayer et al., 1997) ribbon snakes are proposed

for the road extraction in cartographic images, i.e. the

detection of thick lines with a signiﬁcant width. A

ribbon snake is represented by a set of control points

on the centerline and a width at each point forming

two ribbon sides that are forced to be parallel. Ker-

schner (Kerschner, 2003) modiﬁes this approach and

treats the two ribbon sides as separate snakes, called

twin snakes, with an additional attraction force among

each other which are thus relatively independent of

their initial position. This idea is similar to the dual

active contour model, published by Gunn (Gunn and

Nixon, 1997). In order to relax the sensitive choice of

parameters and the snake’s initialization nearby the

desired edges, they use two interlinked contours. One

contour expands from inside the target object while

the other one contracts from the outside. By the

means of an alternating deformation process the cou-

pled snakes try to reach the same equilibrium. That

way, even weak local minima can be rejected.

Ziplock snakes were introduced by Neuenschwan-

der (Neuenschwander et al., 1997). Only the two end

points of the open snake must be speciﬁed by the op-

erator, but exactly on the desired curve. The snake is

ﬁrst approximated with a straight line between these

points. Beginning at the end points, gradually the

vertices are activated to optimize their position, i.e.

take part in the deformation process which is ﬁnished

when all vertices are movable and the snake stabilizes.

One further drawback of classical snakes is their

topological inﬂexibility. Geometric active contours,

developed independently by Caselles (Caselles et al.,

1993) and Malladi (Malladi et al., 1995), are based

on the theory of curve evolution and geometric ﬂows.

Using a level set based implementation (Osher and

Sethian, 1988), the contours can easily split and

merge in the deformation process. A parametric ac-

tive contour model, that solves this problem, is the

topologically adaptable snake model, called T-Snake

which was presented by McInerney (McInerney and

Terzopoulos, 1995). There, a simplicial grid is super-

posed over the image domain which is used to iter-

atively reparameterize the deforming active contour,

also allowing a dynamical change in topology.

Due to the different problems associated with

snakes, an adaption of the model is required for each

special case. This paper summarizes some existing

approaches and some new aspects of speeding up the

snake deforming algorithm that are applied in our im-

plementation. It comprises a multiresolution strategy,

the use of multithreading techniques, subdividing the

snake into segments and a detailed description how to

compute one iteration step in O(n) instead of O(n

2 ACTIVE CONTOUR MODELS

A snake is a unit speed curve ~v : [0, 1]

→ R

with

~v(s) = (x(s), y(s))

that deforms on the spatial do-

main of an image by minimizing the following energy

functional:

E =



∂~v

∂s



+ β



∂

∂s



ext

(~v)ds (1)

where α and β are positive weighting parameters. The

ﬁrst two terms belong to the internal energy E

int

con-

trolling the smoothness of the snake while the external

energy E

ext

= E

img

+ E

con

consists of a potential

energy E

img

providing information about the image

and possibly a constraint energy E

con

The image energy E

img

deﬁnes a potential ﬁeld

with low values at the desired image features. For

the edge extraction of an image I the following term

is often used (Xu and Prince, 1997):

img

(x, y) = −κ|∇(G

(x, y) ∗ I(x, y))|

(2)

where G

is a two-dimensional Gaussian function

with the standard deviation σ, ∇ is the gradient op-

erator and κ is a positive weighting parameter.

User interactions are often desirable to inﬂuence

the deformation, e.g. if an active contour is trapped

in a local energy minimum. Formulations of the con-

straint energy E

con

can be used to integrate an indi-

vidual behavior. Kass proposed user-deﬁned points,

called springs and volcanos, that attract and push

away snakes. These points are useful instruments to

control a snake in the deforming process.

Using the calculus of variations a curve that mini-

mizes the integral (1) has to satisfy the Euler equation:

∂

∂s

− β

∂

∂s

− ∇E

ext

0 (3)

This is often taken as a force balance equation:

int

ext

0 (4)

with

int

= α

∂

∂s

−β

∂

∂s

and

ext

img

con

−∇E

ext

. Treating ~v as function of time and dis-

cretization of the equation (3) by approximating the

snake as a polygon and the partial derivatives as ﬁ-

nite differences, a solution can be found iteratively as

follows (Kass et al., 1987):

(t+1)

= (A+γI)

−1

(γ~v

(t)

−

img

(~v

(t)

)−

con

(~v

(t)

))

(5)

where ~v

(t)

is the vector of control points of the snake

at time step t, ~v

(t+1)

at time step t + 1 respectively,

A is a quadratic iteration matrix according to the di-

mension of the snake vector containing elements that

are linear combinations of α and β, I is the identity

matrix and γ is a positive weighting parameter con-

trolling the step size of each iteration which can be

considered as viscosity parameter.

VISAPP 2006 - IMAGE ANALYSIS

324

2.1 Extending Abilities

Due to the limited capture range of the image forces

and the sensitivity of local minima an initial contour

must be placed very close to the desired object bound-

aries. This is one of the most important disadvantages

of classical snakes.

One approach diminishing that problem was pub-

lished by Xu and Prince (Xu and Prince, 1997). The

replacement of the classical image force formulation

by a vector ﬁeld, they called Gradient Vector Flow

(GVF), provides a larger attraction range by the pres-

ence of boundary information in homogeneous re-

gions. They deﬁne an Edge Map f(x, y) derived from

the image I(x, y) having large values at the features

of interest, e.g. image edges:

f(x, y) = |∇(G

(x, y) ∗ I(x, y))|

(6)

Note, the ﬁeld ∇f has vectors pointing to the image

edges, but still with a narrow capture range. The GVF

ﬁeld ~g(x, y) = (u(x, y), v(x, y))

is calculated in the

next step by minimizing the energy functional:

E =

µ(u

)+|∇f |

|~g−∇f |

dxdy

(7)

The energy is dominated by the partial derivatives of

the vector ﬁeld in homogeneous regions where |∇f |

is small, yielding a smooth ﬁeld. |∇f| is large at im-

age edges and there E is minimal when ~g = ∇f . µ

is a positive weighting parameter which should be in-

creased the more noisy the image is. A possible way

to ﬁnd a solution of equation (7) was described in (Xu

and Prince, 1998). Finally the potential force

img

equation (5) is replaced by the GVF term −~g.

Figure 1 illustrates the diffusion of the image gradi-

ent considering a simple U-shaped object as example.

The enlarged attraction range of image edges sim-

pliﬁes the active contour’s convergence into concave

boundary regions. Further on, the immediate close-

ness of initial contours to the desired object bound-

aries is not necessary any longer. But the advantages

of this method are bought dearly by the expensive

computation of the GVF ﬁeld, especially with huge

images. We observed, GVF snakes produced more

qualitative results in our tests if a Gaussian ﬁlter was

applied to the image.

Cohen (Cohen, 1991) proposed a balloon model to

solve the problems encountered with the limited cap-

ture range of image edges while using the traditional

image energy. To allow an expansion of active con-

tours they introduced an inﬂation force:

= w

~n(s) (8)

where ~n(s) is the unit normal vector of the oriented

contour at the point ~v(s) and w

is a weighting pa-

rameter that controls the inﬂuence of that force. Ap-

plying this pressure force, as an additional part of the

(b)

(a) (b)

Figure 1: Image forces. (a) Traditional potential force ﬁeld.

(b) Gradient Vector Flow ﬁeld.

constraint forces

con

, the curve behaves like a bal-

loon, that is inﬂated. So it counteracts the snake’s

tendency to shrink under the predominant inﬂuence of

the elasticity force. Inﬂating active contours are also

able to detect closed object contours not only from

outside with the implicit aid of the shrinking behav-

ior but also from inside. Using this pressure force the

snake can easier move into concave boundary regions.

Changing the sign of w

makes the snake deﬂating

instead of inﬂating. An adequate choice of w

can

speed up the convergence process, particularly when

strong edges should be detected.

3 SPEEDING UP METHODS

This section describes the different methods for a fast

semiautomatic segmentation using snakes. The re-

search at the Georg August University of G

ottingen

often deals with image sizes of more than 100

megapixels. Therefore an efﬁcient implementation is

essential for a proﬁtable practical use.

3.1 Acceleration of Initial

Computations

Once the potential image forces are determined, they

can be used for the entire segmentation process with-

out recalculation. In order to speed up the computa-

tion of the Edge Map and the GVF we take advantage

of current processor architectures that support the par-

allel execution of multiple arithmetical ﬂoating point

operations. However properly memory aligned data is

necessary for fast loading and storing instructions in

order to gain an noticeable acceleration. In fact load-

ing and storing time could slow down the computation

in spite of parallel execution due to unaligned data.

Further on, we use separate background threads for

their computation, particularly the GVF, which is very

SPEEDING UP SNAKES

325

time expensive for huge images like those from the re-

search in G

ottingen. This saves a little time because

in the meantime the user is able to perform indepen-

dent tasks like setting up one or more initial contours

or adjusting parameter values.

3.2 Multiresolution with an

Automation Approach

We use a multiresolution approach which is very sim-

ilar to Leroy (Leroy et al., 1996). After a huge im-

age has been loaded several smaller scales of the im-

age are computed. Each scale has half the width

and height of the above scale. This computation is

repeated until the coarsest image size is about one

megapixel.

Starting with a rough initial contour with a few

points in the coarsest scale, we can set up an iter-

ative process. By solving small systems of linear

equations our approach determines a suitable solu-

tion curve very rapidly. Furthermore, the tendency to

shrink is stronger if the active contour has only a few

points, due to the structure of the internal forces, i.e.

the snake needs less iterations. A simple polygonal

initialized snake is ﬁlled with many collinear points

on the edges of the polygon. If these points are lo-

cated in regions without a potential image force they

have a minimal energy. So they will not move unless

a discrete curvature is present which can be found,

of course, at the polygon’s vertices. That means that

these vertices are the ﬁrst deforming parts of the snake

spreading a smaller curvature to their neighbors. One

can imagine that the snake is shrinking faster the less

points it has. In fact, this behavior can be desired,

though it is commonly seen as a disadvantage. Often,

a snake has to move across regions without any edge

information when detecting object boundaries from

outside by contraction. Therefore, it has to deform

while being exposed only to the internal forces.

In order to keep an approximate point distance, new

points are inserted when switching to a higher resolu-

tion next to scaling the contour to an appropriate size.

That means the result of the last lower scale is used

as the initial curve for the current scale. When the

original resolution is reached the snake should be al-

ready very close to the desired curve and therefore

only a few iterations are needed for a more detailed

extraction. This approach leads to an acceleration,

because the biggest distance of the contour is covered

in coarse scales with only a few points and in higher

scales just minimal reﬁnements are needed.

User interaction can be further reduced if accept-

able results can be achieved without the need of pa-

rameter adjustments during the deforming process.

Based on that multiresolution strategy, we have de-

signed an automation technique, that allows an auto-

matic image segmentation for images with a sufﬁcient

quality. We start with a given initial contour in the

coarsest scale with the traditional image forces (no

GVF). Besides we use the opposite image forces for

the beginning convergence process, i.e. using

img

instead of −

img

in equation (5). That way, we can

keep the snake slightly distant from the desired object

boundaries. Otherwise we observed the contour of-

ten moving across weak edges in lower scales. The

deformation procedure automatically switches to the

next scale after the snake has stabilized its position.

It is scaled to double size and additional points are

inserted. For each reached scale the potential im-

age forces are recomputed, according to the new size.

These steps are repeated until we reached the original

size of the image. Then the classical image energy

(with the correct sign) or the GVF ﬁeld is used for

the last time the deforming process gets started. Con-

verged close to the desired edges in the meantime the

snake can now ﬁt to them very quickly.

3.3 Using Segments

Kerschner (Kerschner, 2003) proposed an approach

that uses segments in order to overcome local min-

ima. A trafﬁc light system enables the snake to diag-

nose the quality of the segmentation result of itself.

Thereby segments in different colors (red for rejected

results, yellow for unsure results, green for trustwor-

thy results) are presented to the operator who can in-

ﬂuence the accepting procedure of the automatic rat-

ing system. Typically, yellow and red parts are linked

and deform afterward with a modiﬁed energy func-

tion, e.g. by changing parameter values.

We use segments to gain another acceleration. Dur-

ing the deforming process parts of a snake often reach

the desired object boundaries faster than others, e.g.

an active contour has not moved into an concave

boundary region yet while the rest of the object has

been detected already. Points in these parts will not

move anymore and thus can be excluded from the it-

erative minimization procedure. This can be done by

subdividing the snake into segments and treating them

as open snakes.

The segmentation process is started with one seg-

ment – one closed contour. The movement of each

point of the snake is traced for the last few iterations.

If the position of several adjacent points does not

change signiﬁcantly within that time, two segments

are formed. The ﬁrst segment contains these adja-

cent points and is locked, i.e. is ignored in the future

minimization process. The second segment is ﬁlled

with the remaining points and further on deforming

as open snake by solving a respectively smaller sys-

tem of equations. Figure 2 shows the use of segments.

VISAPP 2006 - IMAGE ANALYSIS

326

(a) (b) (c)

Figure 2: Segments. (a) Rough initial contour. (b) First

segments are formed. (c) Approximately 90% of the desired

curve are already detected. Only 10% of the vertices are

included in the computation.

3.4 Fast Implementation

For the computation of one single iteration step a

system of linear equations (Kass et al., 1987) has to

be solved. We write the system (5) as ~y = B~x.

B ∈ R

n×n

is a sparse matrix with a band structure

for both closed and open snakes where n is the num-

ber of control points of the snake. In this section we

describe an efﬁcient O(n) algorithm to solve that sys-

tem for both cases.

We assume α and β being constant along the whole

curve. According to the deﬁnition of ﬁnite differ-

ences, we set:

a := β

b := −α − 4β

c := 2α + 6β + γ

3.4.1 Closed Snakes

In compliance with cyclic boundary conditions, i.e.

the knot vector ~v of the contour is periodically con-

tinued, all ﬁnite differences are computable. Thus, B

has the shape:

B =







c b a a b

b c b

a b c

b a

a b c b a

a b

c b a

b c b

b a a b c







We now subdivide the symmetric matrix B as follows:

B =



E F



(9)

where E ∈ R

(n−2)×(n−2)

, F ∈ R

(n−2)×2

and H ∈

2×2

are also matrices and E is invertible. Note E

is really pentadiagonal. With the Schur complement

S := H − F

−1

F of E in B we can factorize the

matrix:

B =



E 0



I E

−1

0 I



(10)

where I is the identity matrix of an appropriate size.

In order to solve the system ~y = B~x in O(n), we

perform the following steps.

1. Compute Cholesky’s decomposition of the matrix

E = LL

in O(n) (see algorithm 1 in the appen-

dix). Note, L is a lower triangular matrix and has

the lower bandwidth 2, i.e. l

= 0 as i > j + 2.

2. Compute the matrix Q

of the equation LQ

= F .

A solution of that matrix equation can be found by

solving the systems L~q

, (i = 1, 2) by an

optimized forward substitution in O(n) (see algo-

rithm 2 in the appendix) where ~q

and

are the

i-th column vectors of Q

and F .

3. Compute the matrix Q of the equation L

Q = Q

the same way by an optimized backward substitu-

tion in O(n) (analogous to forward substitution).

Now Q = E

−1

F is determined.

4. Compute the Schur complement S = H − F

Now we split the vector ~x = [~x

, ~x

]

, where ~x

∈

(n−2)

and ~x

∈ R

. All other vectors are split anal-

ogous, yielding with equation (10):



E 0



I Q

0 I









For the determination of ~x, some steps remain:

5. Compute ~w

by solving E ~w

= ~y

6. Set ~w

= ~y

− F

7. Compute ~x

by solving S~x

= ~w

8. Set ~x

= ~w

− Q~x

Finally, the solution of B~x = ~y is determined. Note,

the steps 1–4 are only needed if one of the parameters

or the size of the system (n) changes by the inser-

tion or deletion of vertices. The steps 5–8 have to be

performed after each iteration. The complexity of all

steps is O(n), except the steps 6 and 7 which can be

computed in O(1). Thus, the overall complexity for

all steps is O(n).

3.4.2 Open Snakes

Open snakes need other boundary conditions. We re-

peat twice the ﬁrst vertex at the beginning and the last

vertex at the end of the snake’s knot vector ~v. Again,

all ﬁnite differences are computable. Now the matrix

SPEEDING UP SNAKES

327

B has the following shape:

B =







˜c b a

b c b

a b c

b a

a b c b a

a b

c b a

b c

a b ˜c







where ˜c = a + b + c and

b = a + b. Note, B

is not symmetric anymore and thus, we cannot use

Cholesky’s decomposition. Instead, we can use an

optimized LU decomposition of B = LU , because

B is completely pentadiagonal. Then, the solution of

the system B~x = ~y can be found as follows:

1. Compute the LU decomposition of B = LU in

O(n) (see algorithm 3 in the appendix). Note, L

is again a lower triangular matrix with the lower

bandwidth 2, and U is an upper triangular matrix

respectively with the upper bandwidth 2.

2. Compute ~w by solving L~w = ~y using again an op-

timized forward substitution.

3. Compute ~x by solving U ~x = ~w using again an op-

timized backward substitution.

The LU decomposition has to be recomputed each

time the parameters or the number of vertices change.

All of the steps have a linear complexity and thus, the

overall computation has the complexity O(n), too.

3.5 Memory Saving by Scaling

The semiautomatic segmentation of huge images us-

ing snakes needs a lot of memory, especially for the

precalculation of the image’s potential energy, such as

the traditional image energy or the GVF. However, it

is desirable, that the image next to all necessary data

structures ﬁts into physical memory.

We store the Edge Map and the Edge Map’s gra-

dient internally scaled in a lossy format in order to

be able to handle larger images. In either case, the

Edge Map gradient will be needed, because it is the

starting point for the GVF computation and also the

traditional image forces can be derived directly from

it. Typically, ﬂoating point values use 32 bit for single

or 64 bit for double precision. We only use 16 bit.

Let x

∈ [x

min

, x

max

], i = 1, . . . , n be n ﬂoating

point values. In order to represent these values using

16 bit, they can be scaled to integer values of the in-

terval [0, 65535] using the encoding function f

and

the decoding function f

) =



− x

min

max

− x

min

· 65535



(11)

) =

65535

· (x

max

− x

min

) + x

min

(12)

min

and x

max

must be stored as 32 bit or 64 bit ﬂoat-

ing point values, while the storage of the n integer

values y

only needs 16 bit each with.

The storage of the Edge Map needs one and its gra-

dient two ﬂoating point values per pixel. Using the

introduced scaling method we save 3 bytes per pixel.

Considering an image with 100 megapixels, we would

save 300 MB.

Of course, that approach slows down the computa-

tion of these structures, because at the beginning the

minimal and maximal values have to be determined

and elements need to be decoded in order to access

them. That is why this method was not applied to

the GVF, because the permanent encoding, decoding

and redetermination of x

min

and x

max

slowed down

its computation disproportionately, while the deceler-

ation, caused by the implementation for the Edge Map

and its gradient, is tolerable.

This technique leads to another speedup, because a

larger amount of data can be kept in physical memory,

instead of swapping out portions on a slow secondary

storage when reaching the memory limit.

4 RESULTS

Synthetic situations were created, to test the different

speeding up methods.

We optimized our implementation by the use of

SSE

instructions. Due to the memory alignment

condition, these techiques were not applied to all cal-

culations. Actually, the time for the determination of

the Edge Map and the GVF could be considerably de-

creased to approximately 30%.

Table 1 points out the importance of an optimized

implementation. It shows the time of a naive O(n

)

implementation of the solution of the system (5) us-

ing the LU decomposition, confronting the optimized

O(n) version, described in section 3.4.

Figure 3 shows a histological section of the re-

search in G

ottingen with the original size of 3900 ×

4120 pixels. The time for achieving the result (3b),

was measured in different scales of the same image,

starting from the same initial contour (3a), but with

different number of vertices respectively. The results

are presented in table 2.

All results were achieved on an Intel Pentium IV

2.4GHz processor with 1GB DDR-RAM.

VISAPP 2006 - IMAGE ANALYSIS

328

Table 1: Comparison between naive and optimized imple-

mentation. 1000 deforming steps were calculated in each

case. The times neither include the costs of the precompu-

tation of the Edge Map nor the costs for the GVF.

vertices O(n

) O(n) factor

256 1 min 36 s 4.8 s 20

512 23 min 25 s 8.6 s 166

1024 6 h 28 min 11.2 s 2079

2048 - 22.4 s -

4096 - 52.8 s -

(a) (b)

Figure 3: A histological section scaled at

size. (a) Rough

initial contour. (b) Deformation to the approximate convex

hull of the object.

Finally, the introduced techniques were applied to

detect the outer contour of the object of the histo-

logical section in ﬁgure 4a. The image with a size

of 9100 × 15965 pixels was preprocessed with some

image ﬁlters and scaled to 3376 × 5923 pixels (4b)

so that the GVF and the image itself ﬁt into mem-

ory. The ﬁnal contour (4c), has 1555 vertices and was

achieved after 2 minutes and 15 seconds and 5660 it-

erations (without the computational time for the po-

tential forces). Assuming two vertices per second

can be set by hand, a manual segmentation would

have taken approximately 15 minutes. The deform-

ing process comprises four image scalings and a ﬁne

tuning of the result by the insertion of some springs.

5 CONCLUSION

In this article, we presented different methods of

speeding up the semiautomatic image segmentation

process using parametric active contour models. Aim-

ing the replacement of the tedious manual segmen-

tation by a faster semiautomatic segmentation for

the medical research at the University of G

ottingen,

we developed a graphical user interface combining

these techniques with other improving approaches

Table 2: Times and deforming steps to achieve the result of

ﬁgure 3b in different scales.

scale vertices iterations time

12.5% 130 563 1.1 s

25% 240 2113 10.5 s

50% 480 8867 1 min 20 s

100% 950 35269 10 min 5 s

(a) (b) (c)

Figure 4: (a) Original image. (b) Filtered and scaled image

with initial contour. (c) Final result after interactions.

that were already published, such as the Gradient Vec-

tor Flow and the balloon model which are popular

extensions of the traditional snake model providing a

larger attraction range. This research deals with huge

images and thus an efﬁcient and memory saving im-

plementation is desirable to justify the practical appli-

cation.

It was shown how important it is, to take advantage

of the band structure of the underlying matrices. Also

the multiresolution method leaded to a considerable

acceleration due to the fast convergence in coarser

scales. Using segments is advantageous for the ﬁ-

nal reﬁnement steps, e.g. in the original scale of the

image where many successfully detected parts of the

snake can be excluded from the calculation.

Because of dealing with those huge images, mem-

ory saving approaches are also very important, like

the scaling of the values of the traditional potential

energy. Further approaches reducing the memory us-

age would be useful, especially for the storage of the

Gradient Vector Flow.

APPENDIX: ALGORITHMS

All of the shown algorithms were used to achieve

O(n) complexity for one single iteration step.

SPEEDING UP SNAKES

329

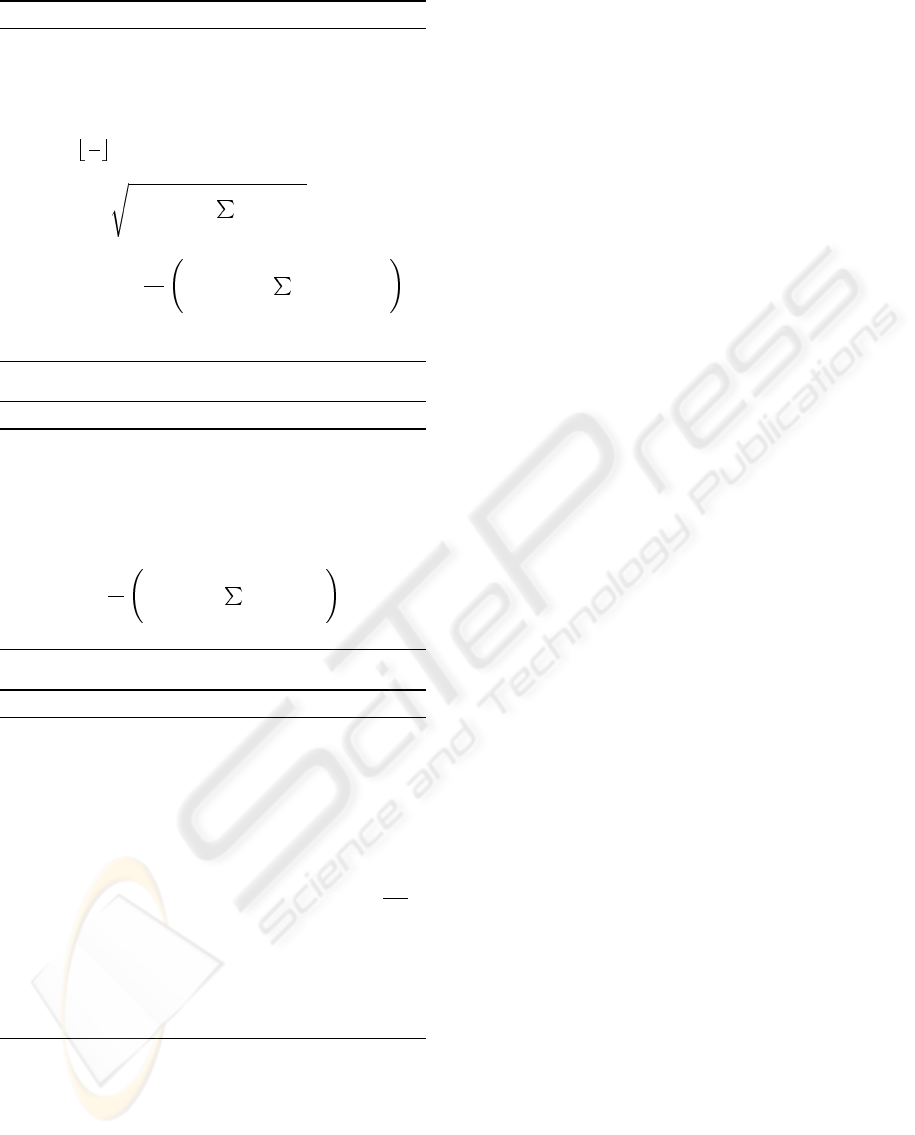
Algorithm 1: Efﬁcient Cholesky decomposition

Input : Symmetric band matrix A = (a

)

n,n

i=1,j=1

with the bandwidth w.

Output : Cholesky decomposition of the matrix

A = LL

. A will be overwritten with the

elements of the matrix L.

←

for i ← 1 to n do

← a

−

i−1

k=max{1,i−w

}

for j ← i+1 to min{i+w

, n} do

←

−

i−1

k=max{1,j−w

}

end

Algorithm 2: Efﬁcient forward substitution

Input : Lower triangular matrix L = (l

)

n,n

i=1,j=1

with the lower bandwidth w

, result vector

b = (b

, . . . , b

)

Output : Solution vector ~x = (x

, . . . , x

)

of the

system L~x =

for i ← 1 to n do

←

−

i−1

j=max{1,i−w

}

end

Algorithm 3: Efﬁcient LU decomposition

Input : Band matrix A = (a

)

n,n

i=1,j=1

with the

lower and upper bandwidth w

and w

Output : LU decomposition of the matrix A = LU.

A will be overwritten with elements of the

lower triangular matrix L below and with

elements of the upper triangular matrix U

above of and upon the main diagonal.

for k ← 1 to n do

for i ← k+1 to min{k+w

, n} do a

←

for j ← k+1 to min{k+w

, n} do

for i ← k+1 to min{k+w

, n} do

← a

− a

end

REFERENCES

Caselles, V., Catte, F., Coll, T., and Dibos, F. (1993). A geo-

metric model for active contours. Numerische Mathe-

matik, 66:1–31.

Cohen, L. D. (1991). On active contour models and bal-

loons. CVGIP: Image Understanding, 53(2):211–218.

Gunn, S. R. and Nixon, M. S. (1997). A robust snake im-

plementation; a dual active contour. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

19(1):63–68.

Kass, M., Witkin, A., and Terzopoulos, D. (1987). Snakes:

Active contour models. International Journal of Com-

puter Vision, 1(4):321–331.

Kerschner, M. (2003). Snakes f

ur Aufgaben der digi-

talen Photogrammetrie und Topographie. Disserta-

tion, Technische Universit

at Wien.

Leroy, B., Herlin, I. L., and Cohen, L. D. (1996). Multi-

resolution algorithms for active contour models. In

Proceedings of the 12th International Conference

on Analysis and Optimization of Systems Images,

Wavelets and PDE’S, Rocquencourt (France).

Malladi, R., Sethian, J. A., and Vemuri, B. C. (1995).

Shape modeling with front propagation: A level set

approach. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 17(2):158–175.

Mayer, H., Laptev, I., Baumgartner, A., and Steger, C.

(1997). Automatic road extraction based on multi-

scale modeling, context, and snakes. In Theoretical

and Practical Aspects of Surface Reconstruction and

3-D Object Extraction, volume 32, Part 3-2W3, pages

106–113.

McInerney, T. and Terzopoulos, D. (1995). Topologically

adaptable snakes. In Fifth International Conference

on Computer Vision, pages 840–845. IEEE Computer

Society.

Neuenschwander, W. M., Fua, P., Iverson, L., Szkely, G.,

and K

ubler, O. (1997). Ziplock snakes. International

Journal of Computer Vision, 25(3):191–201.

Osher, S. and Sethian, J. A. (1988). Fronts propagating

with curvature-dependent speed: algorithms based on

hamilton-jacobi formulations. Journal of Computa-

tional Physics, 79(1):12–49.

Perrin, D. P. and Smith, C. E. (2001). Rethinking classical

internal forces for active contour models. In IEEE In-

ternational Conference on Computer Vision and Pat-

tern Recognition, pages II: 354–359.

Rueckert, D. and Burger, P. (1996). A multiscale approach

to contour ﬁtting for mr images. In SPIE Confer-

ence on Medical Imaging: Image Processing, volume

2710, pages 289–300. SPIE.

Xu, C. and Prince, J. L. (1997). Gradient vector ﬂow: A new

external force for snakes. In Proceedings of the 1997

Conference on Computer Vision and Pattern Recogni-

tion (CVPR ’97), pages 66–71. IEEE Computer Soci-

ety.

Xu, C. and Prince, J. L. (1998). Snakes, shapes, and gra-

dient vector ﬂow. In IEEE Transactions on Image

Processing, pages 359–369. IEEE Computer Society.

VISAPP 2006 - IMAGE ANALYSIS

330