ALGEBRAIC CURVES IN PARALLEL COORDINATES
Avoiding the “Over-Plotting” Problem
Zur Izhakian
Tel Aviv University
The School of Mathematical & Computer Science, Ramat Aviv, 69978, Tel Aviv, Israel
Keywords:
Scientific Visualization, Multi-dimensional Geometric Modeling and Algorithms, Parallel Coordinates.
Abstract:
Until now the representation (i.e. modeling) of curve in Parallel Coordinates is constructed from the point
↔ line duality. The result is a “line-curve” which is seen as the envelope of it’s tangents. Usually this
gives an unclear image and is at the heart of the “over-plotting” problem; a barrier in the effective use of
Parallel Coordinates. This problem is overcome by a transformation which provides directly the “point-curve”
representation of a curve. Earlier this was applied to conics and their generalizations. Here the representation,
also called dual, is extended to all planar algebraic curves. Specifically, it is shown that the dual of an algebraic
curve of degree n is an algebraic of degree at most n(n − 1) in the absence of singular points. The result that
conics map into conics follows as an easy special case. An algorithm, based on algebraic geometry using
resultants and homogeneous polynomials, is obtained which constructs the dual image of the curve. This
approach has potential generalizations to multi-dimensional algebraic surfaces and their approximation. The
“trade-off” price then for obtaining planar representation of multidimensional algebraic curves and hyper-
surfaces is the higher degree of the image’s boundary which is also an algebraic curve in -coords.
1 PARALLEL COORDINATES
Over the years a methodology has been developed
which enables the visualization and recognition of
multidimensional objects without loss of informa-
tion. It provides insight into multivariate (equiva-
lently multidimensional) problems and lead to several
applications. The approach of Parallel Coordinates
(abbr. -coords) (Inselberg, 1985) is in the spirit of
Descartes, based on a coordinate system but differing
in an important way as shown in Fig 1. On the Euclid-
ean plane R
2
(more precisely on the projective plane
P
2
) with xy-Cartesian coordinates, n copies of a real
line, labelled
¯
X
1
,
¯
X
2
,...,
¯
X
n
, are placed equidistant
and perpendicular to the x-axis with
¯
X
1
and y being
coincident. These lines, which have the same orienta-
tion as the y-axis, are the axes of the Parallel Coor-
dinate system for the n-dimensional Euclidean space
R
n
. A point C =(c
1
,c
2
,...,c
n
) ∈ R
n
is repre-
sented by the polygonal line
¯
C having vertices at the
values c
i
on the X
i
-axes. In this way a one-to-one
correspondence is established between a points in R
n
and planar polygonal lines with vertices on the paral-
lel axes. The polygonal line
¯
C contains the complete
lines and not just the segments between adjacent axes.
y
x
X
n
X
n-1
X
n-2
X
i+1
X
i
X
i-1
X
2
X
1
X
1
. . .
. . .
c
n
c
n- 1
c
n- 2
c
i+ 1
c
i
c
i- 1
c
2
c
1
c
1
Figure 1: A point C =(c
1
,c
2
,...,c
n
) ∈ R
n
is rep-
resented by the polygonal line
¯
C (consist of n − 1 sec-
tions) with vertices at the c
i
values of the
¯
X
i
axis for
i =1, 2,...,n.
The restriction to R
2
provides that not only is a
point represented by a line, but that a line is repre-
sented by a point. The points on a line are represented
by a collection of lines intersect at a single point as
can be seen in Fig. 2; i.e. a “pencil” of lines in
the language of Projective Geometry. A fundamental
point ↔ line duality is induced which is the corner-
150
Izhakian Z. (2006).
ALGEBRAIC CURVES IN PARALLEL COORDINATES Avoiding the “Over-Plotting” Problem.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 150-157
DOI: 10.5220/0001356601500157
Copyright
c
SciTePress

X
1
y
x
x
2
x
1
X
2
l
l
l
Figure 2: Fundamental point ↔ line duality.
X
1
y
x
x
2
x
1
X
2
γ
γ
Figure 3: Point-curve mapped into line-curve (envelope of
lines).
stone of deeper results in -coords. The multidimen-
sional generalizations for the representation of linear
p-flats in R
n
(i.e. planes of dimension 1 ≤ p ≤ n−1),
in terms of indexed points have been obtained. The
proper setting for dualities is the projective P
2
rather
than the Euclidean plane R
2
. A review of the mathe-
matical foundations is available in (Inselberg, 1999).
For non-linear, especially non-convex, objects the
representation is naturally more complex. In R
2
a point-curve, a curve considered as collection of
points, is transformed into a line-curve; a curve pre-
scribed by it’s tangent lines as in Fig. 3. The line-
curve’s envelope, a point-curve, is the curve’s image
in -coords. In many cases this yields an image that is
difficult to discern. This point requires elaboration in
order to motivate and understand some of the devel-
opment presented here. As posed, the construction of
a curve’s image involves the sequence of operations:
point − curve → line − curve −→
point−curve (as the envelope of line− curve).
Unlike the example shown in Fig. 3, where the
line-curve’s image is clear, the plethora of overlap-
ping lines obscures parts of the resulting curve-line.
This is a manifestation of what is sometimes called
“over-plotting” problem in -coords; the abundance
P
P
γ
γ
Figure 4: In line-curve (on the left) the tangents cover the
image shown on the right as a point-curve.
X
1
y
x
x
2
x
1
X
2
γ
γ
Figure 5: Point-curve mapped into point-curve.
of “ink” in the picture covers many underlying pat-
terns. Simply our eyes are not capable of “extracting”
the envelope of lots of overlapping lines. There are
also computational difficulties involved in the direct
computation of the image curve’s envelope. In a way
this is the “heart” of the “over-plotting” problem con-
sidered as a barrier in the effective use of -coords.
This problem can be overcome by skipping the inter-
mediate step and go to an equivalent
point − curve −→ point − curve
transformation which provides directly a clear image.
as shown in Fig. 5.
This point-to-point mapping (Inselberg Transfor-
mation (Inselberg, 1985) ) preserves the curve’s con-
tinuity properties. The idea is to use the → part of the
duality and map the tangents of the curve into points
as illustrated in Fig. 5. Therefore, a curve is repre-
sented by a point-curve (the “dual curve”) in the -
coords plane. For a point-curve, γ, defined implicitly
by
γ : f(x
1
,x
2
)=0. (1)
the x, y coordinates of the point-curve image (i.e.
ALGEBRAIC CURVES IN PARALLEL COORDINATES – Avoiding the "Over-Plotting" Problem
151
dual) ¯γ are given by
⎧
⎨
⎩
x =
∂f/∂x
2
(∂f/∂x
1
+∂f/∂x
2
)
,
y =
(x
1
∂f/∂x
1
+x
2
∂f/∂x
2
)
(∂f/∂x
1
+∂f/∂x
2
)
.
(2)
It was shown by B. Dimsdale (Dimsdale, 1984) and
generalized in (Inselberg, 1985), using this transfor-
mation that conics are mapped into conics in 6 differ-
ent ways (Dimsdale, 1984). Here we develop the ex-
tension of the dual image for the family of general al-
gebraic curves. This family of curves is highly signifi-
cant in many implementations and applications, since
these curves can easily and uniquely be reconstructed
from a finite collection of their points (for instance
using simple interpolation methods (Burden, 1989),
(Walter, 1997)). Approximations of such curves can
simply be obtained using similar methods.
As will be seen, the dual of an algebraic curve
in general has degree higher than the original curve.
There are some fringe-benefits, illustrated later,
where “special-points” such as self-intersections or
inflection-points which are conveniently transformed.
But we do not want to get ahead of ourselves. The key
reason for this effort is to pave the way for the repre-
sentation of algebraic curves and more general hyper-
surfaces, as well as their approximations, in terms of
planar regions without losing information. To pursue
this goal then we need firstly to study the image of
curves starting with general algebraic curves.
2 TRANSFORMS OF
ALGEBRAIC CURVES
2.1 The Idea Leading to the
Algorithm
In order to represent non-linear relations in -coords
it is essential to extend the representational results
first to algebraic curves; those described by either,
explicitly or implicitly by irreducible polynomials of
arbitrary degree. The direct application of eq. (2)
turns out to be difficult even for degree 3. There is a
splendid way to solve this problem using some ideas
and tools from Algebraic Geometry. These involve
properties of homogeneous polynomials and Resul-
tant which are explained during the development of
the method. For extensive treatments the reader is re-
ferred to (Cox, 1997), (Hariss, 1992), (Hodge, 1952)
and (Walker, 1978).
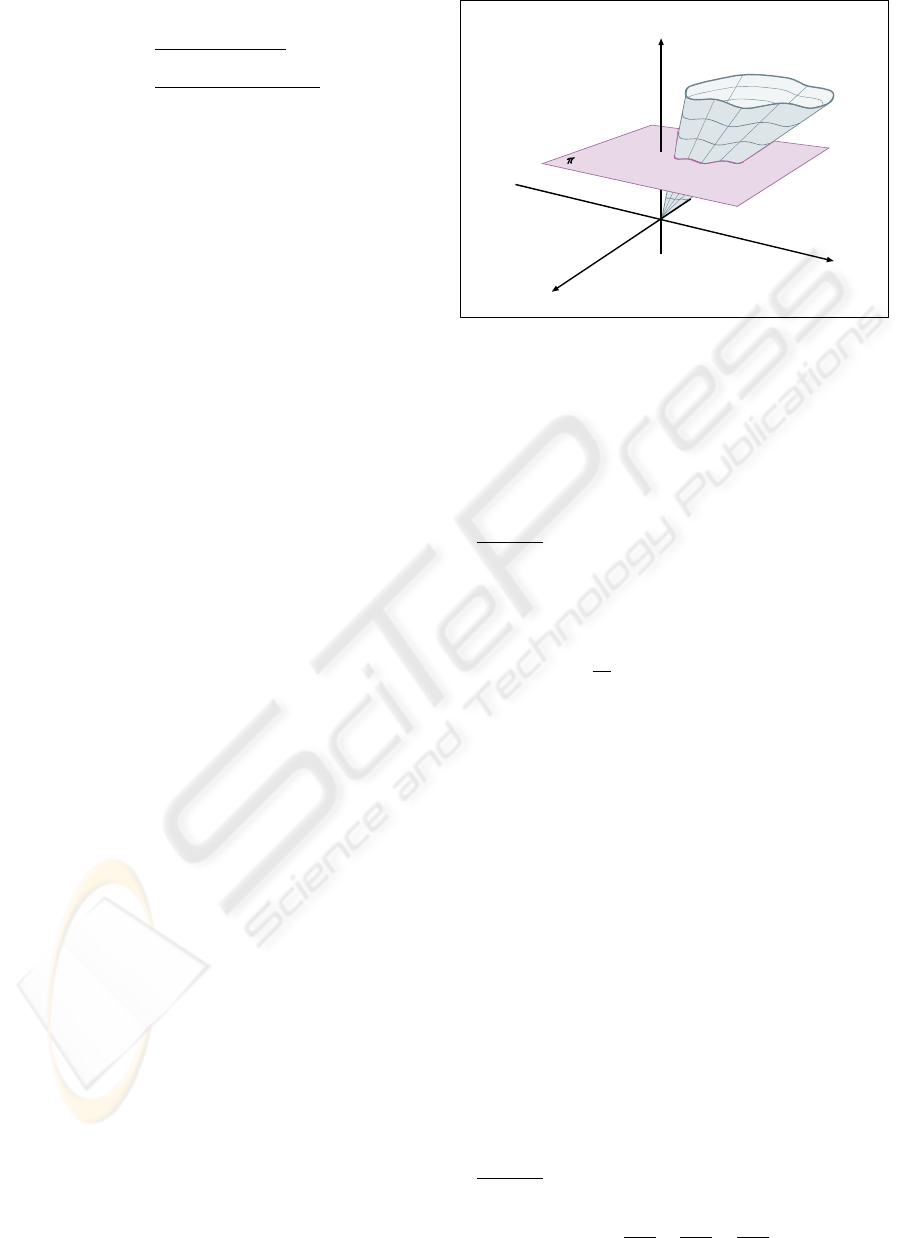
Starting with an algebraic curve γ defined by an
irreducible polynomial f (x
1
,x
2
)=0in R
2
its im-
age in -coords is sought. A number of preparatory
steps smooth the way for the easier application of the
transformations in eq. (2). First the curve γ ⊂ R
2
is
),,(
321
xxxF
3
x
)(
2
RP
),(
21
xxf
1:
3
=
x
2
x
1
x
Figure 6: Cone F (x
1
,x
2
,x
3
)=0generated by embed-
ding the curve f(x
1
,x
2
)=0in P
2
.
“raised” to a surface embedded in the projective space
P
2
and only then the corresponding mapping into -
coords is applied.
Step 1:
There exists a one-to-one correspondence
(preserving the reducibility of polynomials) between
any polynomial f(x
1
,x
2
)=0of degree n and a
homogenous polynomial in the projective plane P
2
,
which is obtained by using homogeneous coordinates.
Specifically,
• replace x
k
by
x
k
x
3
for k =1, 2,
• multiply the whole polynomial by x
3
n
and sim-
plify.
These multiplications are, of course, allowable for
x
3
=0. The result is a homogeneous polynomial
(which is also irreducible if f =0is) with each term
having degree n. To wit,
f(x
1
,x
2
)=
n
i+j=0
a
ij
x
i
1
x
j
2
→
F (x
1
,x
2
,x
3
)=
n
i+j=0
a
ij
x
i
1
x
j
2
x
n−i−j
3
, (3)
which describes a surface in P
2
where the original
polynomial curve is embedded as:
f(x
1
,x
2
)=F (x
1
,x
2
, 1). (4)
Step 2:
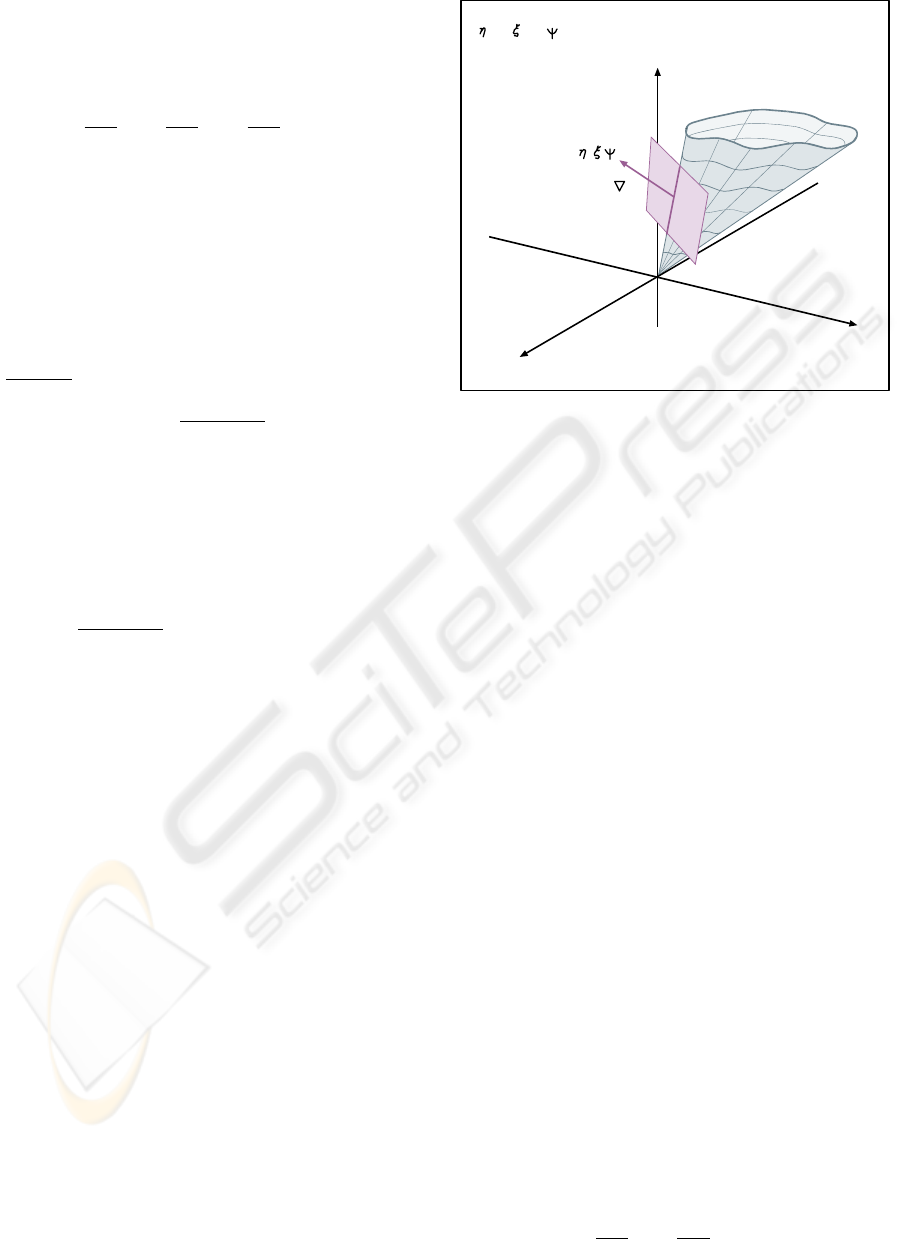
The Gradient of F is found and denoted
by :
∇F (x
1
,x
2
,x
3
)=(
∂F
∂x
1
,
∂F
∂x
2
,
∂F
∂x
3
)=(η, ξ, ψ).
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
152
The three derivatives provide the direction numbers
of the normal to the tangent plane at the point
(x
1
,x
2
,x
3
) . It is a fundamental property of homoge-
neous polynomials that
x
1
∂F
∂x
1
+ x
2
∂F
∂x
2
+ x
3
∂F
∂x
3
= nF (5)
where n is the degree of F . In our case F =0and
hence the equation of the tangent planes is
ηx
1
+ ξx
2
+ ψx
3
=0. (6)
Since the tangent plane at any point of the surface
goes through the origin it is clear that the surface F is
a cone with apex at the origin as shown in Fig. 6.
Step 3:
Substituting for x
3
from eq. (6) in
F (x
1
,x
2
, −(
ηx
1
+ ξx
2
ψ
)) = 0. (7)
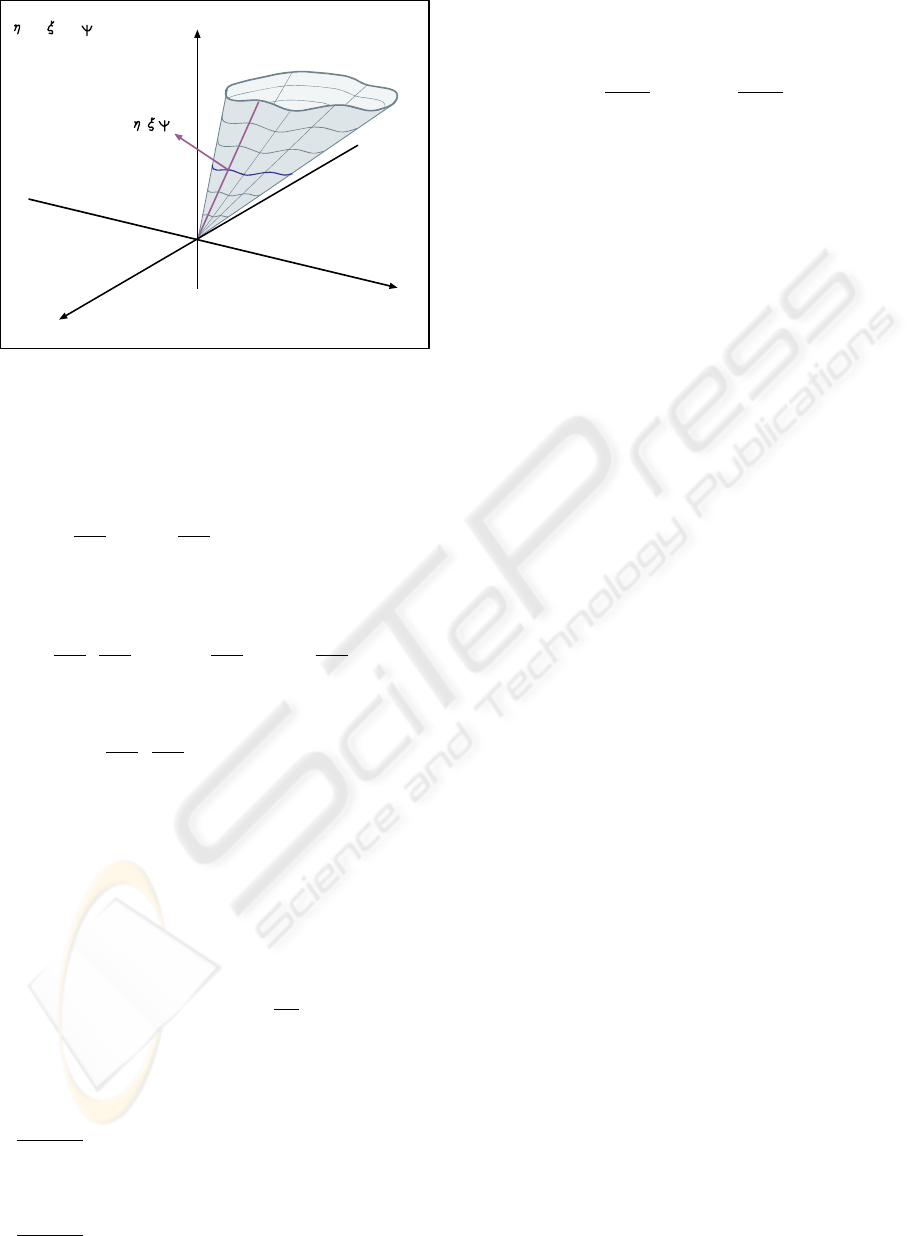
provides the intersection of the tangent plane with the
cone which is a whole line as shown in Fig. 7. Each
one of these lines, of course, goes through the origin
and therefore it can be described by any one other of
its points and in particular by (x
1
,x
2
, 1). Simplifying
the homogeneous coordinates by,
(x
1
,x
2
, −(
ηx
1
+ ξx
2
ψ
)=(ψx
1
,ψx
2
, −(ηx
1
+ξx
2
))
results in
F (ψx
1
,ψx
2
, −(ηx
1
+ ξx
2
)) = 0. (8)
By the way, this is also a homogeneous polynomial
in the five variables appearing in its argument. It is
helpful to understand the underlying geometry. Eq.
(8) can be considered as specifying a family of lines
through the origin (0, 0, 0) and through each point
(x
1
,x
2
, 1) along the curve given by eq. (4). Alterna-
tively, the cone can be considered as being generated
by a line, the generating line – see Fig. 8, pivoted at
the origin and moving continuously along each point
(x
1
,x
2
, 1) of the curve described by eq. (4). On each
one of these lines the direction numbers (η, ξ, ψ) are
unique and constant as shown in Fig. 8; i.e. there is a
one-to-one correspondence:
(x
1
,x
2
, 1) ↔ (η, ξ, ψ).
Eq. (7), and hence it’s rephrasing eq. (8), contains
two equivalent descriptions of the cone, i.e. in terms
of the coordinates (x
1
,x
2
, 1) and also the direction
numbers (η, ξ, ψ). Hence one can be eliminated and
as it turns out it is best to eliminate the x
i
,i=1, 2
something which is very conveniently done by means
of the Resultant. The resultant R(F, G) of two ho-
mogenous polynomials
),,(
321
xxxF
3
x
2
x
1
x
),(
21
xxf
)(
2
RP
+⋅
1
x
+⋅
2
x
F
,
(
,
)
0
3
=⋅
x
Figure 7: The intersection of the cone F (x
1
,x
2
,x
3
)=0
with any of it’s tangent planes is a whole line. Along such a
line the direction numbers (η, ξ, ψ) are constant and unique.
F (x
1
,x
2
)=
n
i=0
a
i
x
1
i
x
2
n−i
=0 and
G(x
1
,x
2
)=
m
j=0
b
j
x
1
j
x
2
m−j
=0
is the polynomial obtained from the determinant of
their coefficients matrix:
R(F, G)=
Det
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
a
0
a
1
a
2
··· a
n
0
ra
0
a
1
a
n
.
.
.
.
.
.
a
0
··· a
n
b
0
b
1
b
2
··· b
m
b
0
b
2
b
m
.
.
.
.
.
.
0 b
0
··· b
m
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
,
where the empty spaces are filled by zeros. There are
m lines of a
i
and n lines of b
j
. When F and G are
both irreducible so is their resultant. Due to the ho-
mogeneity of F and G,
R(F, G)=0⇔ F =0,G=0.
Let us rewrite eq. (8) as
F
(η,ξ,ψ)
(x
1
,x
2
)=
n
i=0
a
i
(η, ξ, ψ)x
1
i
x
2
n−i
=0.
(9)
Appealing again to the homogeneity of F to obtain
the relation
x
1
∂F
∂x
1
+ x
2
∂F
∂x
2
= nF
ALGEBRAIC CURVES IN PARALLEL COORDINATES – Avoiding the "Over-Plotting" Problem
153
),,(
321
xxxF
3
x
2
x
1
x
),(
21
xxf
)(
2
RP
+⋅
1
x
+⋅
2
x
,
(
,
)
0
3
=⋅
x
)1,,(
21
xx
Figure 8: This shows the generating line of the cone (which
is found from the intersection of the tangent planes with the
cone) together with the gradient vector.
which has already been mentioned earlier. Therefore
∂F
∂x
1
=0 ,
∂F
∂x
2
=0⇒ F =0
and from the property of the resultant of homoge-
neous polynomials mentioned above
R(
∂F
∂x
1
,
∂F
∂x
2
)=0⇔
∂F
∂x
1
=0 ,
∂F
∂x
2
=0.
Altogether then
R(
∂F
∂x
1
,
∂F
∂x
2
)=R(η, ξ, ψ)=0 (10)
has finite degree since F and R are polynomials. It
was shown that
R =0⇔ F =0
so not only their zero sets agree, which ensures that
they are equivalent polynomials, but they also agree
at an infinite number of points. Hence, R =0pro-
vides the description of the cone F =0in terms of
the direction numbers (η, ξ, ψ) and is also a homoge-
neous polynomial. The degree of
∂F
∂x
i
is n − 1. This
and the structure of the resultant with the four trian-
gular zero portions results in R being a polynomial of
degree at most n(n − 1).
Step 4:
Since we are interested in the solutions of
R =0the multiplier in powers of ψ of R, if there is
one, can be safely neglected due to the homogeneity.
Step 5:
Only in this, the final step, the transforma-
tion of the curve from the x
1
x
2
-plane to the xy-plane
with parallel coordinates is performed. It is done us-
ing equations (2) rewritten, in view of eq. (6) as
x =
ξ
η + ξ
,y= −
ψ
η + ξ
. (11)
It is important to notice that both this and eq. (10) in-
volve only the derivatives η, ξ, ψ. Let c = η + ξ,so
that ξ = cx, η = c − cx = c(1 − x) and ψ = −cy.
Substitution provides the transform of the original
curve f(x
1
,x
2
)=0:
R(η, ξ, ψ)=R(c(1 − x),cx,−cy)=
c
n
R((1 − x),x,−y)=0 ⇒
R((1 − x),x,−y)=0,
when c =0. In the previous step it was pointed out
that this polynomial has degree at most n(n − 1), the
actual degree obtained depends on the presence of sin-
gular points in the original algebraic curve f =0.
2.2 Algorithm
Here the process involved is presented compactly as
an algorithm (Izhakian, 2001) whose input is an alge-
braic curve γ : f (x
1
,x
2
)=0and the output is the
polynomial which describes ¯γ, the curve’s image in
-coords. To emphasize, the algorithm applies to im-
plicit or explicit polynomials of any degree and curves
with or without singular points. The formal descrip-
tion of the algorithm is followed by examples which
clarify the various stages and their nuances.
For a given irreducible polynomial equation (oth-
erwise apply the algorithm for each of it’s component
separately) f(x
1
,x
2
)=0.
1. Convert to homogeneous coordinates to obtain the
transformation of f , a homogenous polynomial
F (x
1
,x
2
,x
3
)=0.
2. Substitute
x
1
→ ψx
1
, x
2
→ ψx
2
and
x
3
→−(ηx
1
+ ξx
2
).
3. Find the resultant of the two derivatives F
x
1
and
F
x
2
.
4. Cancel the multiplier in a power of ψ of the resul-
tant R and denote the result by R
.
5. The output is obtained by the substitution
η =1− x, ξ = x, ψ = −y in R
.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
154

3 EXAMPLES OF ALGEBRAIC
CURVES AND THEIR
TRANSFORMS
3.1 Conic Transforms
T he algorithm is illustrated with some examples
starting with the conics.
f(x
1
,x
2)
=
(
x
1
x
2
1
)
A
1
A
4
A
5
A
4
A
2
A
6
A
5
A
6
A
3
x
1
x
2
1
=
A
1
x
2
1
+2A
4
x
1
x
2
+2A
5
x
1
+A
2
x
2
2
+2A
6
x
2
+A
3
=
0.
Applying the algorithm in the sequence given above:
Step 1:
The homogeneous polynomial obtained
from f by using homogeneous coordinates is
F (x
1
,x
2
,x
3
)=
A
1
x
2
1
+2A
4
x
1
x
2
+2A
5
x
1
x
3
+
A
2
x
2
2
+2A
6
x
2
x
3
+ A
3
x
2
3
=0.
Step 2:
Substituting
x
1
→ ψx
1
,x
2
→ ψx
2
,x
3
→−(ηx
1
+ ξx
2
)
yields
F (ψx
1
,ψx
2
, −(ηx
1
+ ξx
2
)) =
(−2A
5
ψη + A
1
ψ
2
+ A
3
η
2
)+x
1
2
2(−A
5
ψξ + A
3
ξη + A
4
ψ
2
− A
6
ψη)x
1
x
2
+
(A
2
ψ
2
− 2A
6
ψξ + A
3
ξ
2
)x
2
2
=
c
1
x
1
2
+2c
2
x
1
x
2
+2c
3
x
2
2
=0,
where c
i
= c
i
(η, ξ, ψ), for i =1, 2, 3.
Step 3:
Calculate the two derivatives of F and
their resultant:
∂F
∂x
1
=2c
1
x
1
+2c
2
x
2
,
∂F
∂x
2
=2c
2
x
1
+2c
3
x
2
,
R(
∂F
∂x
1
,
∂F
∂x
2
)=Det
2c
1
2c
2
2c
2
2c
3
=
R(η, ξ, ψ)=
4ψ
2
[
A
3
A
2
− A
2
6
η
2
+
A
1
A
3
− A
2
5
ξ
2
+
A
1
A
2
− A
2
4
ψ
2
+2(A
5
A
6
− A
3
A
4
)ηξ+
2(A
5
A
4
− A
1
A
6
)ξψ +2(A
4
A
6
− 2A
5
A
2
)ηψ.
Step 4:
Retain the resultants component which is
multiplied by a power of ψ and let
R
(η, ξ, ψ)=
R(η,ξ,ψ)
4ψ
2
.
Step 5:
The dual of f(x
1
,x
2
)=0is then given in
matrix form by
X
1
y
x
x
2
x
1
X
2
γ
γ
Figure 9: An ellipse is mapped into hyperbola.
R
(1 − x, x, −y)=
(
xy1
)
a
1
a
4
a
5
a
4
a
2
a
6
a
5
a
6
a
3
x
y
1
,
where the individual a
i
are :
a
1
= A
3
(A
1
+ A
2
+2A
4
) − (A
5
+ A
6
)
2
,
a
2
= A
1
A
2
− A
4
2
,
a
3
= A
2
A
3
− A
6
2
,
a
4
= A
6
(A
1
+ A
4
) − A
5
(A
2
+ A
4
),
a
5
= A
6
2
+ A
5
A
6
− A
3
(A
2
+ A
4
),
a
6
= A
2
A
5
− A
4
A
6
.
The result is illustrated for the ellipse in fig 9 and
can also be contrasted to the earlier ways for obtaining
the transformation
conic ↔ conic.
3.2 Algebraic Curves of Degree
Higher than Two
N ext the algorithm is applied to the algebraic curve
of 3rd degree
f(x
1
,x
2
)=x
3
1
− x
2
1
− x
2
2
+ x
2
− 1=0.
Step 1:
The homogeneous polynomial obtained
from f by using homogeneous coordinates is
F (x
1
,x
2
,x
3
)=x
3
1
−x
2
1
x
3
−x
2
2
x
3
+x
2
x
2
3
−x
3
3
=0.
Step 2:
Substituting
x
1
→ ψx
1
,x
2
→ ψx
2
,x
3
→−(ηx
1
+ ξx
2
)
yields
F (ψx
1
,ψx
2
, −(ηx
1
+ ξx
2
)) =
(ψ
3
+ ψ
2
η − η
3
)x
1
3
+
ALGEBRAIC CURVES IN PARALLEL COORDINATES – Avoiding the "Over-Plotting" Problem
155
X
1
y
x
x
2
x
1
X
2
γ
γ
γ
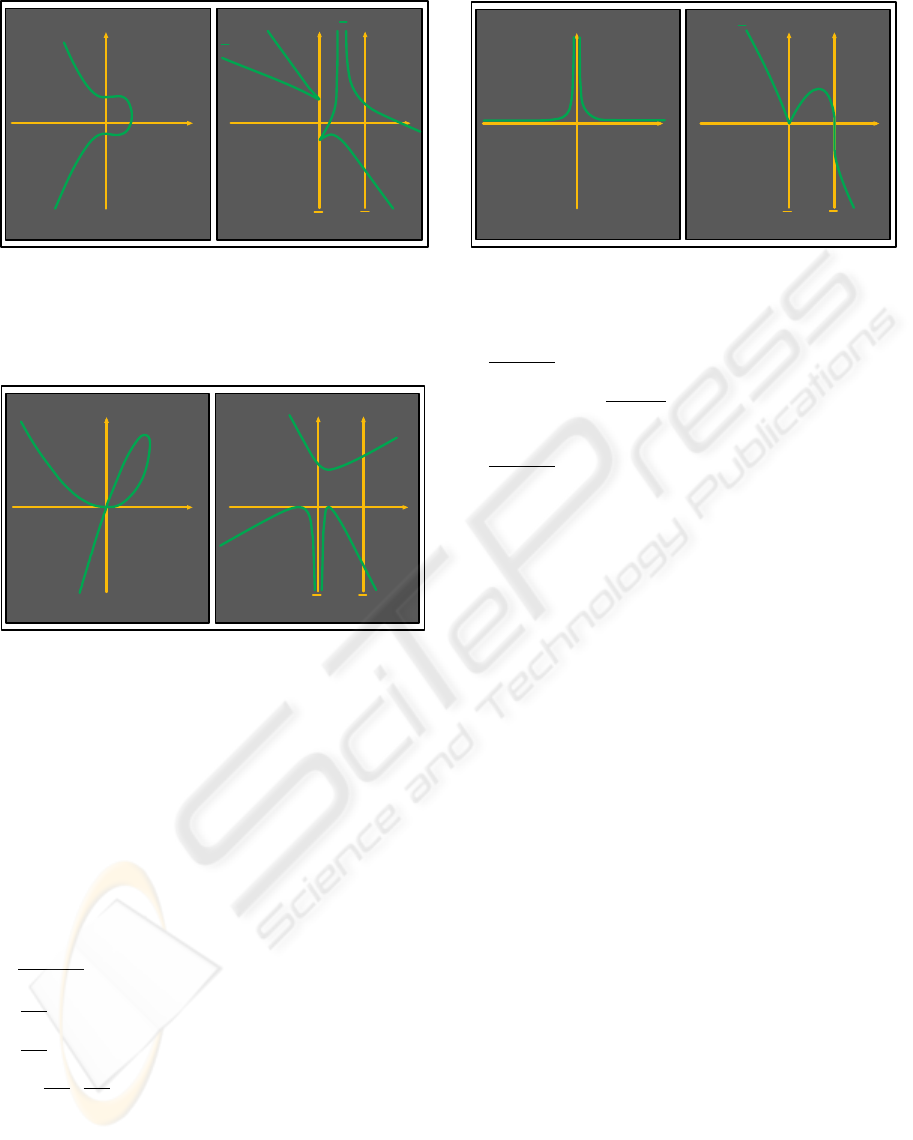
Figure 10: The cubic curve x
3
1
− x
2
1
− x
2
2
+ x
2
− 1=
0 (on the left) is mapped into a six degree curve (on the
right). Notice also an instance of the duality inflection-point
↔ cusp [4].
X
1
y
x
x
2
x
1
X
2
Figure 11: The self intersection point in the cure x
3
1
+
x
2
2
−3x
1
x
2
=0(on the left), disappears in the image curve
27y
2
− 54y
2
x +27y
2
x
2
− 108y + 270yx − 198yx
2
+
40yx
3
+ 108x
3
− 36x
4
− 81x
2
=0(on the right) .
(−3ξη
2
+ ψη
2
+ ψ
2
ξ)x
1
2
x
2
+
(2ψξη + ψ
2
η − 3ξ
2
η)x
1
x
2
2
+
(−ξ
3
+ ψξ
2
+ ψ
2
ξ)x
2
3
=
c
1
x
1
3
+ c
2
x
1
2
x
2
+ c
3
x
1
x
2
2
+ c
4
x
2
3
=0,
where the c
i
= c
i
(η, ξ, ψ), for i =1, ..., 3.
Step 3:
Calculate the resultant of the two deriva-
tives of F :
∂F
∂x
1
=3c
1
x
1
2
+2c
2
x
1
x
2
+ c
3
x
2
2
,
∂F
∂x
2
= c
2
x
1
2
+2c
3
x
1
x
2
+3c
4
x
2
2
,
R(
∂F
∂x
1
,
∂F
∂x
2
)=
Det
⎛
⎜
⎝
3c
1
2c
2
c
3
0
03c
1
2c
2
c
3
c
2
2c
3
3c
4
0
0 c
2
2c
3
3c
4
⎞
⎟
⎠
=
R(η, ξ, ψ)=−3ψ
6
R
(η, ξ, ψ),
where R
is polynomial of degree 6.
X
1
y
x
x
2
x
1
X
2
γ
γ
Figure 12: x
2
1
x
2
− 1=0 −→ 4y
3
+27x
3
− 27x
2
=0.
Step 4: Discarding the resultant’s factor (−ψ
6
)
i.e. let
R
(η, ξ, ψ)=
R(η,ξ,π)
−3ψ
6
.
Step 5:
Finally, substituting
η =1− x, ξ= x, ψ= −y
results in the 6th-degree curve :
R
(1 − x, x, −y)=
−23 + 292y
2
x
2
− 422x
2
+ 326yx
3
− 146y
2
x
+610x
3
+23y
2
− 27y
4
x
2
+54y
4
x − 27y
4
−22yx
5
− 244y
2
x
3
− 66yx
4
− 420yx
2
−126y
3
x+232yx+214x
5
−499x
4
+90y
3
x
2
+54y
3
+ 156x − 50y − 31x
6
+71y
2
x
4
−14y
3
x
3
. The source and image curve are
shown in Fig. 10. In this case n =3and the max-
imum degree n(n − 1) = 6 is attained. Notice that
this covers as special cases :
– the point ↔ line duality where points (with n =0)
are mapped into lines (with n =1) and vice-versa,
and
– the conics with n =2.
The next two examples show that the image curve
may have degree less than n(n − 1). Apparently the
maximal degree is attained by the image curve in the
absence of singularities in the function or it’s deriva-
tives. The full conditions relating the image’s degree
to less then the maximal are not known at this stage.
Two such examples are shown in the subsequent fig-
ures, Fig. 11 and Fig. 12.
4 CONCLUSIONS
Consider the class S of hyper-surfaces in R
n
which
are the envelopes of their tangent hyper-planes. As
mentioned earlier (Inselberg, 1999) hyper-planes can
be represented in -coords by n − 1 indexed points.
Hence for a hyper-surface σ ∈Seach point P ∈ σ
maps into n − 1 indexed planar points. From this
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
156

it follows that the hyper-surface σ can be mapped
(i.e. represented) by n − 1 indexed planar regions
¯σ
i
composed of these points. Restricted classes of
hyper-surfaces have been represented in this way and
it turns out that the ¯σ
i
reveal non-trivial properties
of the corresponding hyper-surface σ. It has already
been proved that for any dimension Quadrics (alge-
braic surfaces of degree 2) are mapped into planar re-
gions whose boundaries are conics (Izhakian, 2004).
This also includes non-convex surfaces like the “sad-
dle”. There are strong evidence supporting the con-
jecture that algebraic surfaces in general map into pla-
nar regions bounded by algebraic curves. This, be-
sides their significance on their own right, is one of
the reasons for studying the representation of alge-
braic curves. In (Inselberg, 2000) families of approx-
imate planes and flats are beautifully and usefully rep-
resented in -coords. Our results cast the foundations
not only for the representation of hyper-surfaces in
the class (S), but also their approximations in terms
of planar curved regions.
REFERENCES
B. Dimsdale, “Conic transformations and projectivities”,
IBM Los Angeles Scientific Center, 1984, Rep. G320-
2753.
A. Inselberg and T. Matskewich, “Approximated planes
in parallel coordinates”, Vanderbilt University Press,
Paul Sabloniere Pierre-Jean Laurent and Larry L. Shu-
maker (eds.), Eds., 2000, pp. 257–267.
Z. Izhakian, “An algorithm for computing a polynomial’s
dual curve in parallel coordinates”, M.sc thesis, De-
partment of Computer Science, University of Tel Aviv,
2001.
Z. Izhakian, “New Visualization of Surfaces in Parallel Co-
ordinates - Eliminating Ambiguity and Some Over-
Plotting”, Journal of WSCG - FULL Papers Vol.1-3,
No.12, ISSN 1213-6972, 2004, pp 183-191.
A. Inselberg, “The plane with parallel coordinates”, The
Visual Computer, vol. 1, no. 2, pp. 69–92, 1985.
A. Inselberg, “Don’t panic ... do it in parallel!”, Computa-
tional Statistics, vol. 14, pp. 53–77, 1999.
R. L. Burden and J. D. Faires, “Numerical analysis”, 4th
ed, PWS-Kent, Boston, MA, 1989.
D. Cox, J. Little, and D. O’Shea, “Ideals, Varieties, and
Algorithms”, Springer, New York, second ed. edition,
1997.
G. b. Folland, “Real analysis: modern techniques and their
applications”, Wiley, New York, second ed. 1999.
J. Harris, “Algebraic geometry”, A first course, Springer-
Verlag, New York, 1992.
W. Hodge and D. Pedoe, “Methods of algebraic geometry”,
Vol. II. Cambridge: Cambridge Univ. Press, 1952.
R. J. Walker, “Algebraic Curves”, Springer-Verlag, New
York, 1978.
G. Walter, “Numerical analysis : an introduction”,
Birhauser, Boston, 1997.
ALGEBRAIC CURVES IN PARALLEL COORDINATES – Avoiding the "Over-Plotting" Problem
157
