
SURFACE SIMPLIFICATION GUIDED BY MORPH-TARGETS
Uwe Berner, Thomas Rieger
Interactive Graphics Systems Group (GRIS), Department of Computer Science, Technische Universität Darmstadt,
Fraunhoferstr. 5, D-64283Darmstadt, Germany
Keywords: Surface Simplification, Morph-Targets, Quadric Error Metrics, Avatar.
Abstract: Many effective automatic surface simplification algorithms have been developed. These automatic
algorithms create very plausible results in many cases, but at very low levels of detail they do not preserve
the visual appearance of the original model very well. This could be improved if surface simplification
algorithms were able to make use of semantic or high-level meaning of models. The idea of our new method
using a morph-target-based surface simplification is to use distance information inside the morph-targets to
acquire the relative importance of different surface regions without user guidance. Using this additional
input the model is simplified by using modified quadric error metrics.
1 INTRODUCTION
An important field of activity at the Interactive
Graphics Systems Group (GRIS) are conversational
user interfaces where the primary goal is to give the
computer a face to talk with. The goal is the
development of software architectures to shift
complex tasks to human like assistants (avatars)
which can be incorporated on different stationary
and mobile devices like laptops, PDAs and mobile
phones. Our present work deals with scalability of
animation and graphical representation of avatars to
make our system available even on small platforms.
More details are provided in (Berner and Rieger,
2005) and (Rieger, Taponecco and Berner, 2005). In
this paper, we will focus on optimization strategies
for the graphical representation of a conversational
avatar.
During the last years many effective automatic
surface simplification algorithms have been
developed which generate a surface approximation
of fewer polygons from complex models. These
automatic algorithms create very plausible results in
many cases, but at very low levels of detail they do
not preserve the visual appearance of the original
model very well. This could be improved if surface
simplification algorithms were able to make use of
semantic or high-level meaning of models. Kho and
Garland introduced a user-guided mesh
simplification (Kho and Garland, 2003) that allows
the user to selectively control the relative importance
of different surface regions. While this approach
allows to preserve the visual appearance of the
original model well, interaction from the user is
required to achieve this result. The idea of morph-
target-based surface simplification is the usage of
distance information inside the morph-targets to
acquire the relative importance of different surface
regions without user guidance. Using this additional
input data the graphical model is simplified by using
the well known quadric error metrics (Garland and
Heckbert, 1997) as the base simplification
algorithm.
2 BACKGROUND
Many successful methods to simplify a given
complex mesh are based on iterative edge
contraction (Hoppe, 1996, Garland and Heckbert,
1997, Lindstrom and Turk, 1998). These approaches
iteratively collapse edges in increasing order of cost,
not regarding any semantc meaning of a
differentiated region. On the other hand, there are
amongst others three semi-automatic simplification
methods “Zeta” (Cignoni, 1998) , “Semisimp” (Li
and Watson, 2001) and “User-Guided
Simplification” (Kho and Garland, 2003) which are
using user interaction to produce improved
simplification results. Zeta requires a precomputed
sequence of simplifications as input. Users can
selectively refine a model by locally changing error
116
Berner U. and Rieger T. (2006).
SURFACE SIMPLIFICATION GUIDED BY MORPH-TARGETS.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 116-121
DOI: 10.5220/0001355001160121
Copyright
c
SciTePress

thresholds. With Semisimp the user uses a vertex
tree structure to provide segmented simplification.
Now, let’s have a more detailed look at the User-
Guided Simplification. The method of Kho and
Garland modifies an input model in an interactive
manner and produces a simplified version guided by
geomety constraints. They use a quadric based
simplification method as a base algorithm (Garland
and Heckbert, 1997), working in the following way.
A given plane nv+d=0 with unit normal n and
point v defines a quadric Q. Q is
Q=(A,b,c)=(nn
T
,dn,d
2
) (1)
The squared distance of a point v to the plane is:
Q(v)=v
T
Av+2b
T
v+c (2)
and the error at a vertex v to a set of planes is the
sum of squared distances:
Σ Qi(v)=(ΣQi)(v) (3)
During the initialization phase of the algorithm each
vertex is assigned a quadric derived from the normal
and the incident faces. For each possible edge
contraction (v
i
,v
j
)→v
ij
the optimal position and the
contraction cost is computed by:
v
ij
=-(A
i
+A
j
)
-1
(b
i
+b
j
) (4)
and
Q(v
ij
)=Qi(v
ij
)+Qj(v
ij
)=(Qi+Qj)(v
ij
) (5)
The new vertex after the edge collapse accumulates
the quadrics by
Qv
ij
=Qi+Qj (6)
The quality of the approximation is determined by
the order of contractions, respectively by the costs.
The main idea of the algorithm from Kho and
Garland is to guide of the simplification by
manipulating the quadric associated with each
vertex. One way to do this is weighting the quadrics
adaptively. This is done by the user painting on the
surface of the geometric model. Based on this
interactive input, the quadrics are weighted with a
scalar at the initializing step:
Qi←w
i
Qi (7)
Thereby the vertices of the colored regions gain
higher costs than before. Thus the order of
contraction is rearranged via the weights, which are
dependant from the interactively marked regions of
the mesh. You can see an example from Kho and
Garland in Figure 1.
Figure 1: Simplified models, interactively improved.
3 SIMPLIFICATION WITH
MORPH-TARGETS
The key idea behind the animation with morph
targets is to combine different geometries
corresponding to given weights during an animation
(see Figure 2). During a time intervall the weights
are changing and thus the geometric objects will be
animated. In our example the different morph targets
G
1
:”normal shape”, G
2
:”eyes closed” and G
3
:”mouth
smile” were combined regarding different weights
(w
1
, w
2
w
3
) to the resulting geometry G
res
., which
results in a smiling head while closing the eyes.
Using a combination of morph-targets, an avatar
animation system can run different animations, let
the face speak or show emotions. Even all possible
combinations can be activated by choosing the
corresponding weights for the individual geometry.
SURFACE SIMPLIFICATION GUIDED BY MORPH-TARGETS
117
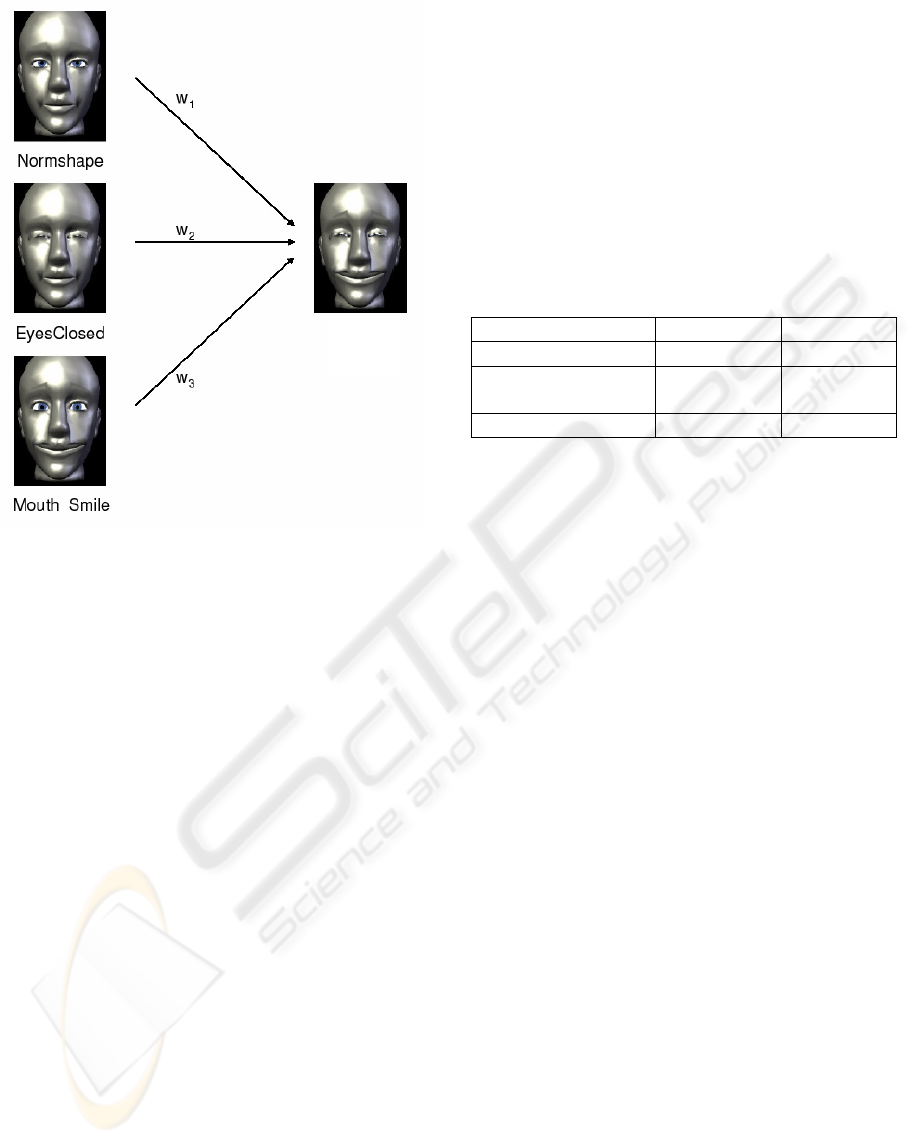
Figure 2: Combination of morph-targets.
The algorithm used for the morph-target-based mesh
simplification is implemented as an extension of the
quadric error metrics algorithm from Garland and
Heckbert using adaptive weighting of quadrics. The
interactive drawing on the mesh from Kho and
Garland is replaced by an automatic procedure based
on the existing morph-targets.
The key idea is that regions with a great distance
between the neutral morph-target and the others are
more animated. This implies more importance for
the visual appearance during an animation.
Therefore, this regions should be presented in more
details after a mesh simplification. This is done by
assigning bigger weights to have bigger contraction
costs and the face would be more detailed at that
regions after the simplification. The differences of
the morph-targets are used to weight the quadrics at
the initialization step. The scalars w
i
in (7) are
computed on the basis of the distances to each
morph-target.
For every vertex the distance D between the
morph-target mt and the neutral morph-target is
computed. Then all the distances belonging to one
vertex are summed up. Thus every vertex is
provided with a distance sum DS.
DS=Σ D
mt
(8)
Now the vertices are sorted by their distances DS
and weights w
i
are given depending on the position
of the vertex inside the resulting order sequence of
vertices.
This is done by grouping the vertices inside three
areas of the sequence. The first of the three with
least distances is weighted with 0.33, the second
with 0.66 and the third with 1.0. This gives for N
vertices:
Index Weights Distances
<= 1/3 N 0.33 small
1/3 N< Index < 2/3
N
0.66 middle
>= 2/3 N 1.0 great
Thus at the initialization step of the simplification
the weighting of the quadrics Qi←w
i
Qi is modified
depending of the distances of the vertices related to
the neutral morph-target. More animated regions
with greater distances get higher weights and
therefore higher contraction costs which implies a
delayed contraction of those areas.
4 RESULTS
The new simplification method was integrated inside
an existing avatar animation system, described in
(Berner, 2004). The animation system is devided in
three components: One for the graphical
representation, one for the speech synthesis and one
for controlling the behavior of the avatar. All these
components are driven from an external dialog
control giving commands to the avatar like “speak
this sentence” or “do this gesture”.
The subject discussed in this paper affects only
the representation component. The complexity of the
animated face could be changed at different levels.
The user has the possibility to select more than ten
different levels of complexity and the system
simplifies the face of the avatar with the quadric
based method of Garland and Heckbert or with our
new morph-target guided simplification. In a later
version of the system the different levels
should be selected automatically depending on the
actual performance conditions. A detailed
description for this method can be found in (Berner
and Rieger, 2005).
G
res
= w
1
*G
1
+w
2
*G
2
+w
3
*G
3
Gres
G
1
G
2
G
3
Table 1: Distance dependent quadric weights.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
118
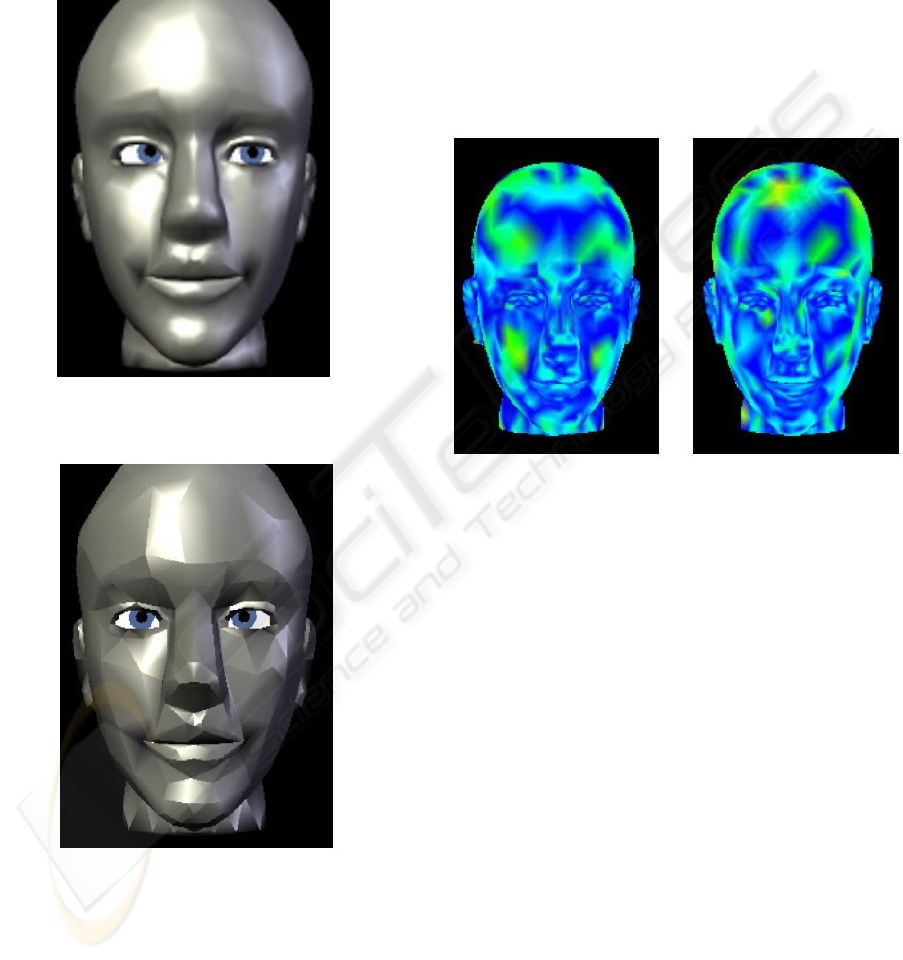
The first idea to evaluate the results was to look
at the reduced heads. But using our present model of
the head, the reduced results were difficult to
distinguish. In Figure 3 the original head with 3128
triangles is shown, in Figure 4 a reduced one with
878 triangles, produced from the running avatar
animation system.
Figure 3: Head, not simplified (3128 triangles).
Figure 4: Head, simplified (878 triangles).
As mentioned, it is not easy to remark the different
results of the two algorithms in an obvious manner.
To compare the results of the different algorithms in
an objective way, we used a tool called MESH
(Aspert et al., 2002), which can compare different
meshes using the Hausdorff-Distance. The
differences between the meshes are colored, blue is a
little difference, green a middle one and yellow a
bigger. We compared the simplified head with the
original and expected a greater discrepancy in the
animated regions using the original algorithm from
Garland and Heckbert. In Figure 5 the comparison
between the basic quadric based algorithm and our
new one is shown. The figure on the right hand side,
is the result of our simplification algorithm where
the head is reduced to 878 triangles. You can see
more blue (dark) areas in the animated regions
defined by the distances of the morph-targets. This is
most obvious at the cheeks.
Figure 5: Comparison of the output.
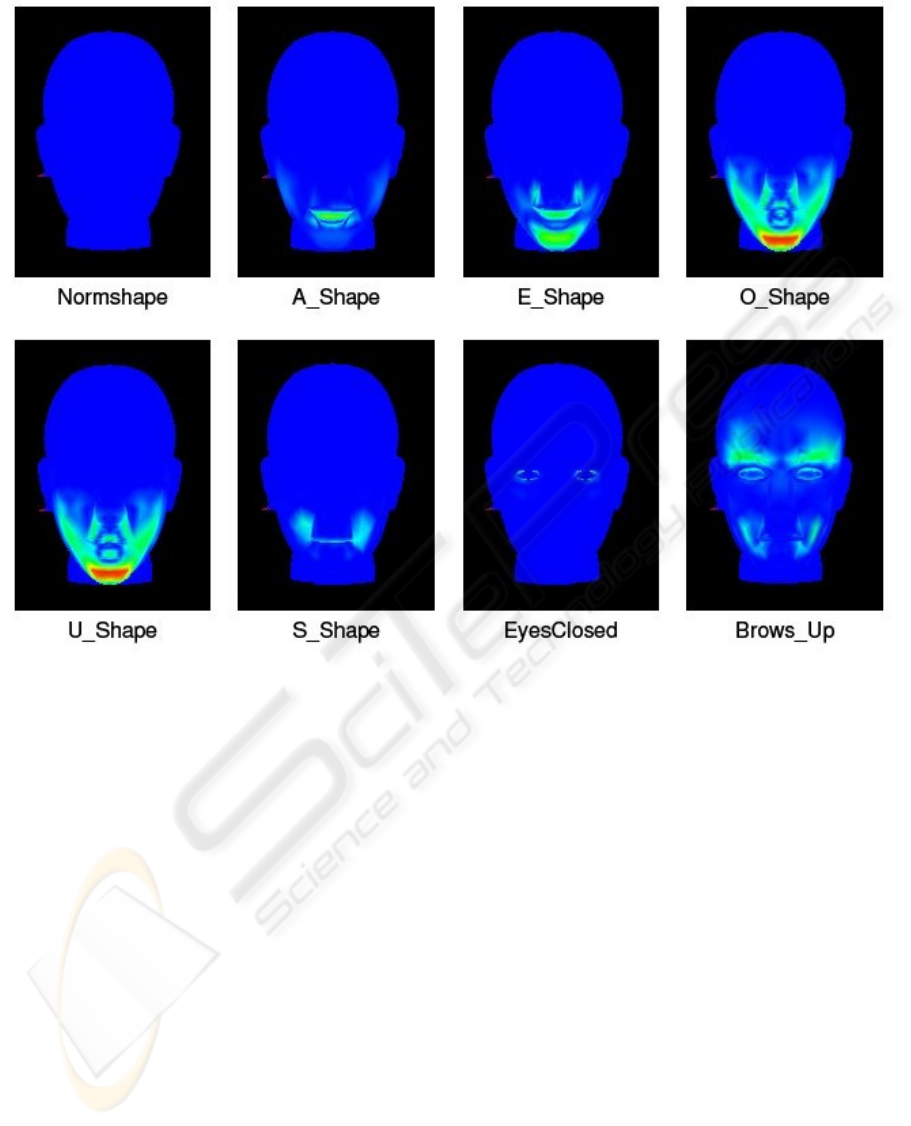
In Figure 6 the differences between the neutral
morph-target and the animated ones are shown.
There you can see, that the cheeks, the chin and the
eyebrows are the most animated regions of the
avatar. And the results above shows that the
animated regions are better approximated than in the
classical algorithm.
SURFACE SIMPLIFICATION GUIDED BY MORPH-TARGETS
119
5 CONCLUSION AND FUTURE
WORK
We have developed an extension of the algorithm
from Kho and Garland presented in the paper “User-
Guided Simplification” (Kho and Garland, 2003).
Our new approach uses the morph-targets related to
the face animation to determine areas which are
highly animated. Using a distance measure the
quadrics of the simplification algorithm are
weighted automatically at the initialization phase.
While our experimental results show that our
idea works satisfactorily, there is still room for
further development in different directions. The
algorithm should be applied to other geometric
models, which are more complex or animate other
regions. Neverthenless it must not be a head. Also
3D scanned datasets should be involved in the
testing of new models.
The strategy of weighting the quadrics should be
more improved, this first one was only implemented
for testing the fundamental method. It can be
advanced for instance by regarding the number of
existing vertices or the total amount of the distances.
Even the function over the order sequence must not
be linear. Another point is, that the not animated, but
relevant regions could be included in the weighting.
This could be the ears or the nose which are relative
important to represent the visual appearance of a
head.
ACKNOWLEDGEMENTS
Our thanks to Eric Hofmann, who did the
measurements, some programming and the graphics.
This work was partially funded by the German
"Bundesministerium für Bildung und Forschung”,
(Federal Ministry of Education and Research)
Figure 6: Comparison of the morph-targets.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
120

through the Research Project Virtual Human, see
(VirtualHuman, 2005).
REFERENCES
Aspert, M., Santa-Cruz, D. and Ebrahimi, T. 2002. MESH:
Measuring Errors Between Surfaces Using The
Hausdorff Distance. In IEEE International Conference
in Multimedia and Expo (ICME)
Berner, U., 2004. Optimized Face Animation with Morph-
Targets. In Proceedings of WSCG 2004.
Berner, U. and Rieger, T. 2005. An Architecture To Adapt
Scalable Virtual Characters. In Proceedings of WSCG
2005.
Cignoni, P., Montani, C.,Rocchini, C., and Scorpigno, R.,
1998. Zeta: A resolution modeling system. GIMP:
Graphical Models and Image Processing 60.
Garland, M. and Heckbert, P.S. 1997. Surface
simplification using quadric error metrics. In
Proceedings of ACM SIGGRAPH 97
Hoppe, H. 1996. Progressive Meshes. In Proceedings of
ACM SIGGRAPH 96
Kho, Y. and Garland, M. 2003. User-Guided
Simplification. In ACM Symposium on Interactive 3D
Graphics.
Li, G. and Watson, B. 2001. Semiautomatic simplification.
In ACM Symposium on Interactive 3D Graphics
Lindstrom, P. and Turk, G. 1998. Fast and memory
efficient polygonal simplification. In IEEE
Visualization 98
Rieger, T., Taponecco, F. and Berner, U., 2005. Multilevel
XML based Behavior Controller for 2d and 3d Virtual
Characters. In Conference on Computational
Intelligence for Modelling, Control and Automation
(CIMCA).
Virtual Human Web-Site 2005. www.virtualhuman.de
SURFACE SIMPLIFICATION GUIDED BY MORPH-TARGETS
121
