DATA PROCESSING AND COMPACT REPRESENTATION OF
MEASURED ISOTROPIC SPECTRAL BRDF
Huiying Xu
Department of Computer Sciences, Purdue University, West Lafayette, Indiana 47907, USA
Keywords: BRDF, Data processing, Representation.
Abstract: This paper presents the methods for both data processing and compact representation of measured isotropic
spectral BRDF. For the data processing, we develop a numerical method for filtering the noises, re-sampling
the data from non-uniform sampling to uniform sampling, and interpolation. For the compact representation,
we propose a method to represent the spectral BRDF in both the spectral and spatial domains. In spectral
domain, for each pair of the incident and outgoing directions, we represent the spectral BRDF with Fourier
coefficients. In spatial domain, for all the outgoing directions of a given incident direction, we represent the
same-order Fourier coefficients either directly using a linear combination of spherical harmonics or a linear
combination of spherical harmonics and a Gaussian, depending on their angular dependencies. Three
Gaussian expressions are presented. Numerical studies are given for a measured isotropic spectral BRDF.
1 INTRODUCTION
Characterizing light reflection from object surfaces
is essential in many areas, such as computer graphics
and visualization, image analysis, remote sensing,
medical imaging, confocal microscopy imaging,
computational simulation, nondestructive inspection,
and etc. The surface light reflections are generally
described by a bi-directional reflection distribution
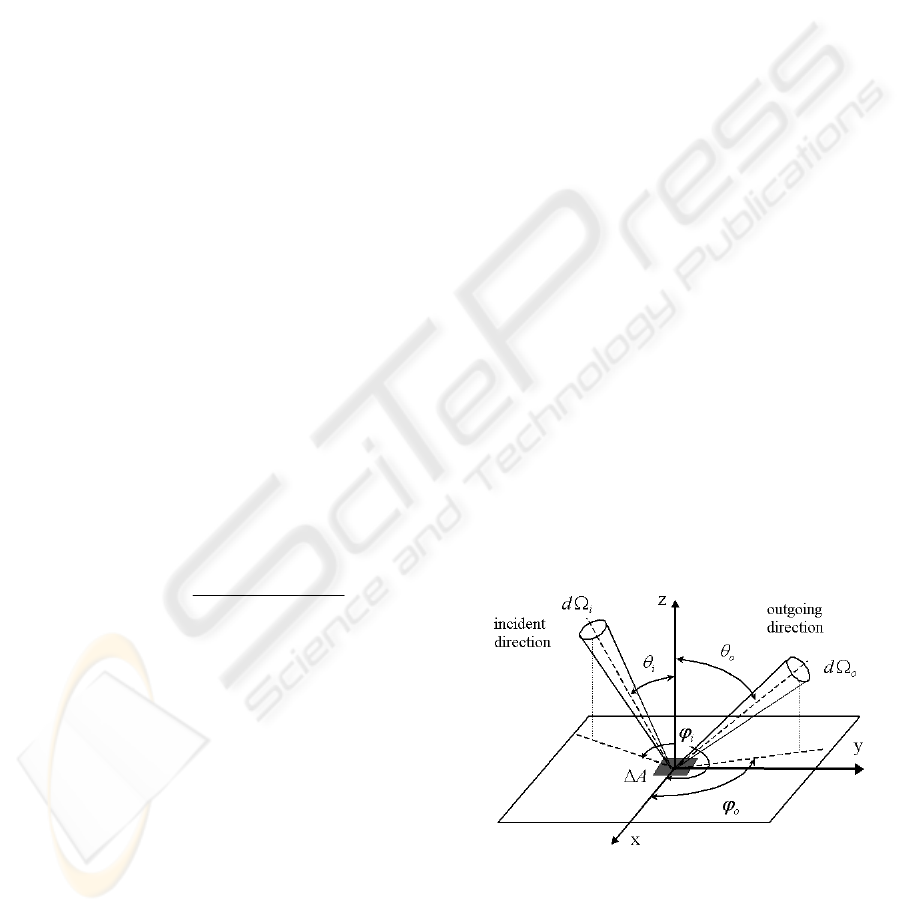
function (BRDF)
(,,)
(,, , ,)
(,,)cos
ooo
iioo
iii i i
dL
Ld
θϕλ
ρθ ϕ θ ϕ λ
θϕλ θ
=
Ω
, (1)
which is the ratio of the reflected radiance
o
dL in
direction
(, )
oo
θ
ϕ
to the incident irradiance
cos
iii
L
d
θ
Ω in solid angle sin
iiii
ddd
θ
θϕ
Ω= (Figure
1), and
λ
is the wavelength. The incident (or
lighting) and outgoing (or viewing) directions are
specified respectively using the angle pairs
(, )
ii
θ
ϕ
and
(, )
oo
θ
ϕ
.
Some analytic models have been developed to
describe surface reflection behavior. However, the
current analytic models were developed based on
various assumptions so that they are not applicable
for all kinds of surfaces. Alternatively, one may
obtain the raw data of BRDFs from the experimental
measurements. However, there are some problems
with the raw data. First, the data has unavoidably
involved the noises so that the data cannot be
directly used. Second, we cannot measure the raw
data for arbitrary pair of incident and outgoing
directions, so we need a method to accurately
interpolate the unmeasured pairs from all the
measured pairs. Third, the measured raw data is
often non-uniformly sampled. However, in some
cases the uniformly sampled data is necessary for
practical application. Fourth, since a spectral BRDF
is a five dimensional function, the storage of raw
data unavoidably occupies a huge space.
Figure 1: The geometry and notations of BRDF definition.
In this paper, we present the methods for both
the data processing and compact representation. For
the data processing, we developed a method to filter
the noises involved in the raw data, resample the
data, and interpolate it for the unmeasured pairs of
407
Xu H. (2006).
DATA PROCESSING AND COMPACT REPRESENTATION OF MEASURED ISOTROPIC SPECTRAL BRDF.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 407-414
DOI: 10.5220/0001352404070414
Copyright
c
SciTePress

incident and outgoing directions. For the compact
representation, we proposed a method to represent
the spectral BRDF. In this method, for each pair of
the incident and outgoing directions, we represent a
BRDF with the Fourier coefficients. For all the
outgoing directions of a given incident direction, we
represent the same-order Fourier coefficients either
directly using a linear combination of spherical
harmonics or using a linear combination of spherical
harmonics and a Gaussian, based on their angular
dependencies. The reconstruction of spectral BRDF
from representation just reverses this process.
This paper is organized as the follows. Section 2
reviews the background. Section 3 elaborates the
data processing method. Section 4 describes the
representation method. Section 5 presents the
numerical studies. Section 6 gives the conclusions
and future work.
2 BACKGROUND
Current analytic models commonly decompose the
entire reflection into the diffuse and specular
components. The diffuse component is typically
assumed to be a Lambertian, but the specular
component varies among models. A simple approach
describes the specular component with the empirical
functions (Phong, 1975; Strauss, 1990). More
accurate models were developed from physically
based approaches. One physically based approach
uses Kirchoff theory with the tangent plane
approximation (Beckmann, 1963). He et al. (1991)
used this approach to model complex effects
including light polarization, surface masking and
shadowing, and subsurface scattering. Another
approach is based on the Torrance-Sparrow
microfacet model of surfaces (Torrance, 1967). This
model assumes that a rough surface is comprised of
many V-shaped planar, perfectly smooth, and
isotropic microfacets. The specular component is
expressed as a product of the Fresnel coefficient, the
masking and shadowing factor, and the surface
orientation probability, as presented in the Blinn-
Cook-Torrance model (Blinn, 1977; Cook, 1982).
An early measurement of BRDFs used gonio-
reflectometer (Murray-Coleman, 1990). However,
the equipment is very expensive, and the
measurement takes very long time. Ward (1992)
introduced a novel device called imaging gonio-
reflectometer. This system uses a half-silvered
hemispherical mirror to collect the light from the
sample surface and reflect it back into a CCD
camera with a fisheye lens. This device is
inexpensive and the measurement is relatively faster.
Dana et al. (1999) developed a simple system to
measure bidirectional texture functions and BRDFs.
Marschner et al. (1999, 2000) constructed a simple
and rapid system to measure isotropic surfaces with
spherical geometry. Matusik et al. (2003a, 2003b)
developed a similar device and measured densely
sampled BRDF data for different materials.
Recently, Sun et al. (2005) measured some spectral
BRDFs by the sample-rotated method. In which, the
spectrum is captured by a PR-650 SpectraScan
colorimeter. During the entire measurement, the
colorimeter is fixed. Instead, the sample is rotated
very often and the light source is relocated several
times for all sampled incident and outgoing
directions.
To save the storage space, it is desirable to
represent the BRDF with fewer parameters. There
are three popular representation methods. The first is
representing a BRDF in terms of an empirical or
physical model (Ward, 1992; Lafortune, 1997). This
method is compact, but inaccurate. The second is
representing a BRDF with a linear combination of a
set of basis functions, such as spherical harmonics
(Carbal, 1987; Sillion, 1991), Zernike polynomials
(Koenderink, 1998), and wavelets (Schröder, 1995;
Lalonde, 1997). The third is factoring a high-
dimensional BRDF into a sum of low-dimensional
functions (Fournier, 1995; DeYong, 1997). The
second and third methods have the same problem:
there exists a trade-off between the accuracy and
compactness. For example, given a BRDF with the
sensitive angular dependency, the larger number of
coefficients is used, the more accurate the
representation, but the less compact.
Most of the previous measurements and
representations focused on the non-spectral BRDF
(such as RGB-based). However, spectral BRDF
offers the better commitment for faithful image
rendering and analysis. Therefore, we need to
develop the correspondent methods for the noises
filtering, data re-sampling, data interpolation, and
compact representation of measured spectral BRDF.
All of these considerations ignite the current work.
3 DATA PROCESSING METHOD
The errors involved in the measurement of spectral
BRDF are diversified. First, for different outgoing
directions, the sample surface viewed by the
colorimeter is different. The larger is the angle
between the surface normal and outgoing direction,
the larger is the area. Since the sample surface is not
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
408
()
f
t
()
f
t
t t
()F
ω
()F
ω
ω
ω
t
()
f
t ()F
ω
ω
()
f
t
0
()
k
tkT
δ
−
∑
0
()
g
nT
strictly smooth and isotropic, the measured spectra
must involve some errors. Second, since the sample,
light source, and colorimeter are rotated or located
manually, this can result in another kind of errors.
Third, the unstable intensity of light source can also
be a source of errors.
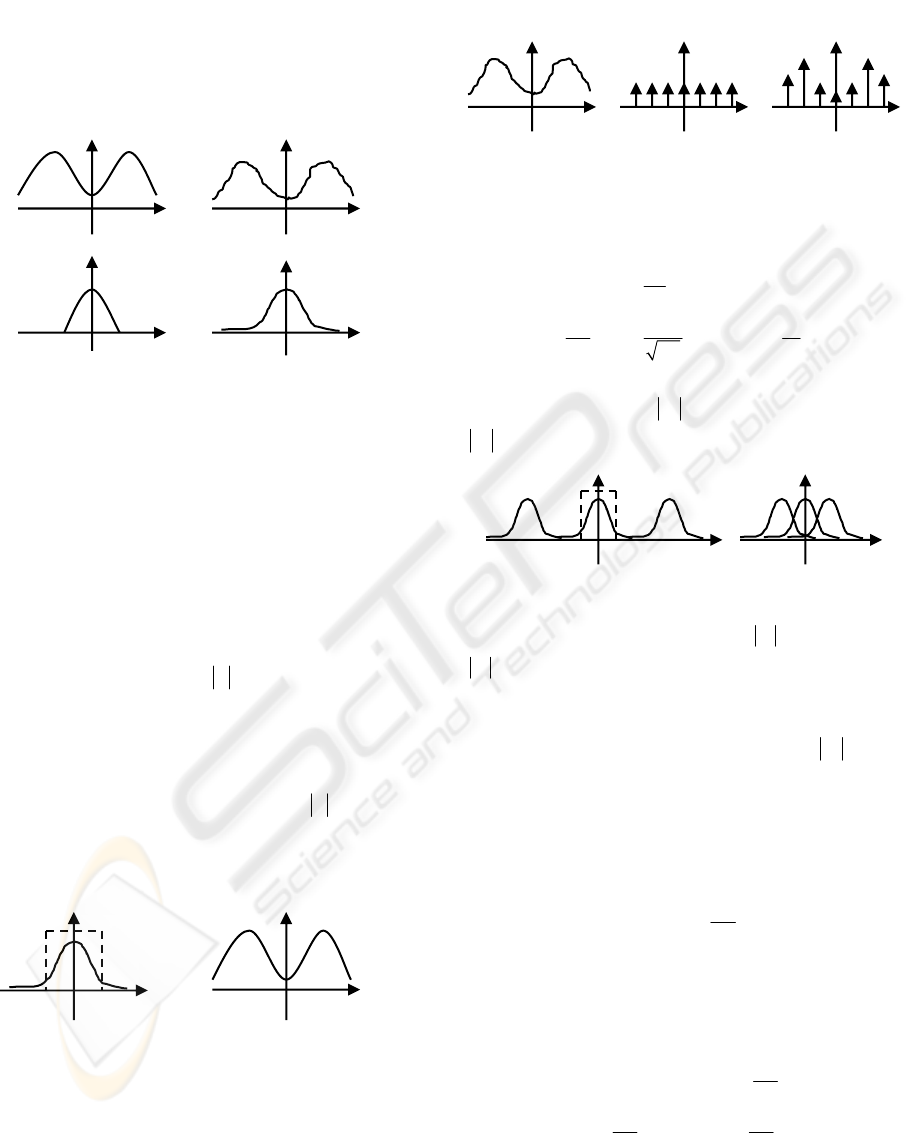
(a) (b)
Figure 2: Fourier transformations of ()
f
t without noises
(a) and with noises (b).
Generally, the contribution of experimental
errors to the measured data oscillates quickly
between the positive and negative effects. Therefore,
we can regard them as the noises that are dominated
by the high frequency components. Consider one-
dimensional case, Fourier transformations of
()
f
t
with and without the noises are shown in Figure 2.
In the subfigure (a), we can find a cut-off frequency
F
ω
so that () 0F
ω
= for
F
ω
ω
>
. However, in the
subfigure (b), it is difficult to find such a cut-off
frequency since the noises contribute wide high
frequency components to the spectrum
()F
ω
.
Therefore, to filter the noises, we can cut off the
high frequency components with
F
ω
ω
> , and
perform inverse Fourier transformation to get the
clean raw data, as shown in Figure 3.
Figure 3: Inverse Fourier transformations for noises
removing.
Given the one-dimensional function
()
f
t , the
uniformly sampled data
0
()
g
nT
with the period
0
T
can be expressed as (Glassner, 1995)
00
() () ( )
k
g
nT f t t kT
δ
=−
∑
. (2)
The sampling process is shown in Figure 4.
Figure 4: Illustration of uniform data sampling.
Using the property of convolution, Fourier
transformation of the sampled data
0
()
g
nT is given
as (Glassner, 1995)
0
() ( )
T
k
GFk
κ
ω
ωω
κ
=−
∑
, (3)
where
0
0
2
T
π
ω
= ,
1
2
κ
π
= , and
0
1
T
T
κ
= .
()G
ω
is
shown in Figure 5. We can see that, copies of
()F
ω
overlap just a little for
0
2
F
ω
ω
> , and quite a lot for
0
2
F
ω
ω
< .
(a) (b)
Figure 5: Illustration of
()G
ω
for
0
2
F
ω
ω
> (a) and
0
2
F
ω
ω
< (b).
To filter the noises from
()
f
t , we need to sample
the raw data with the period
0
T
so that
0
F
ω
ω
> .
Then we can multiply
()G
ω
with a box spectrum
()
F
B
ω
ω
, as dotted line shown in Figure 5(a). Finally
we perform the inverse Fourier transformation to
obtain the filtered
()
f
t . The one-dimensional
expression is given as (Glassner, 1995)
F
00
() ( )sinc ( )
2
n
f
tgnT tnT
ω
π
⎡⎤
=−
⎢⎥
⎣⎦
∑
. (4)
The isotropic BRDF can be described by a four-
dimensional function with the parameters
λ
,
i
θ
,
o
θ
,
and
o
ϕ
. Following Eqs. (2-4), the BRDF for each
component of wavelength is given as
1
1
23
23
(, , ) [,,]sinc[ ( )]
2
sinc[ ( )]sinc[ ( )]
22
ioo i
mn l
oo
W
g
mnl mT
WW
nT lT
λλ
ρθθϕ θ
π
θϕ
ππ
=−
⋅− −
∑∑∑
(5)
where
1
T ,
2
T and
3
T are the sampled periods for
i
θ
,
o
θ
and
o
ϕ
, respectively,
[,,]
g
mnl
λ
is the uniformly
DATA PROCESSING AND COMPACT REPRESENTATION OF MEASURED ISOTROPIC SPECTRAL BRDF
409

sampled data for the grid point (
i
mT
θ
=
,
2o
nT
θ
=
,
3o
lT
ϕ
= ), and
1
1
2
W
T
π
= ,
2
2
2
W
T
π
= , and
3
3
2
W
T
π
= .
Although the raw data of measured spectral
BRDF is non-uniformly sampled and densely
distributed, we can obtain the optimal solution
[,,]
g
mnl
λ
by solving the linear least squares problem
1
1
23
23
2
min [ , , ]sinc[ ( )]
2
sinc[ ( )sinc[ ( )
22
raw i
mn l
oo
W
g
mnl mT
WW
mT mT
λ
ρθ
π
θϕ
ππ
−−
⋅− −
∑∑∑
, (6)
with the constraint
[,,] 0gmnl
λ
≥ . This constraint
comes from the property that the reflectance is non-
negative. We can implement the non-negative least
squares (NNLS) algorithm (Lawson, 1995) to solve
this constrained linear least squares problem.
For the outgoing directions perpendicular to the
sample surface, the BRDF has the property:
33
(,0,0) (,0,) (,0, )
ii i
TlT
ρθ ρθ ρθ
==⋅⋅⋅=
. (7)
In addition, the isotropic BRDF has the property:
33
(0, ,0, ) (0, , , ) (0, , , )
oo o
TlT
ρ
θλρθ λ ρθ λ
==⋅⋅⋅= . (8)
Therefore, we renormalize the matrix in Eq. (6) so
that the optimal solution still satisfies these
properties. Assume that
12
x
x= for the following
linear least squares problem
11 12 13 1 1
21 22 23 2 2
31 32 33 3 3
2
min
aaa x b
aaa x b
aaa x b
⎛⎞⎛⎞⎛⎞
⎜⎟⎜⎟⎜⎟
−
⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠
, (8)
the matrix can be renormalized so that the linear
least squares problem becomes
11 12 13 1
1
21 22 23 2
3
31 32 33 3
2
min
aaa b
x
aaa b
x
aaa b
+
⎛⎞⎛⎞
⎛⎞
⎜⎟⎜⎟
+−
⎜⎟
⎜⎟⎜⎟
⎝⎠
⎜⎟⎜⎟
+
⎝⎠⎝⎠
. (9)
For the outgoing directions far away from the
highlights, the BRDF varies smoothly and gradually.
Hence, the raw data is usually captured sparsely.
However, the sparse data can result in the failure of
solving Eq. (6). To solve this problem, we introduce
the following linear relations into the linear least
squares problem
[ 1,,] 2 [,,] [ 1,,] 0
[, 1,]2 [,,] [, 1,] 0
[,, 1]2 [,,] [,, 1] 0
gm nl gmnl gm nl
gmn l gmnl gmn l
gmnl gmnl gmnl
λλλ
λλλ
λλλ
−− ++=
−− + +=
−− + +=
. (10)
It is obvious that the optimal solution is
uniformly sampled. To interpolate the BRDF for any
unmeasured pair of incident and outdoing directions,
we just need to follow Eq. (5).
4 REPRESENTATION METHOD
Our representation method consists of two stages. In
the first, we represent the spectral BRDF in the
spectral domain. In the second, we represent the
Fourier coefficients in spatial domain.
4.1 Spectral Domain
For each pair of incident and outgoing directions, a
spectral BRDF is a spectrum. Therefore, we perform
Fourier transformation to it and represent it with
Fourier coefficients. The expression is given as
0
min
1
min
1
(, , ,) (, , )
2
2( )
(, , )cos
2( )
(, , )sin
ioo ioo
kioo
k
kioo
a
k
a
k
b
ρθθϕλ θθϕ
πλλ
θθϕ
λ
πλλ
θθϕ
λ
=
=
⎧
−
⎡
⎤
+
⎨
⎢
⎥
∆
⎣
⎦
⎩
⎫
−
⎡⎤
+
⎬
⎢⎥
∆
⎣⎦
⎭
∑
(11)
where
max min
λ
λλ
∆
=− is the visible range, and
max
min
max
min
min
min
2
(, , ) (, , ,),
2( )
cos , 0,1, ,
2
(, , ) (, , ,),
2( )
sin , 1,2, ,
kioo ioo
kioo ioo
ad
k
k
bd
k
k
λ
λ
λ
λ
θθϕ λρθθ ϕ λ
λ
πλλ
λ
θθϕ λρθθ ϕ λ
λ
πλλ
λ
=
∆
−
⎡⎤
⋅
=∞
⎢⎥
∆
⎣⎦
=
∆
−
⎡⎤
⋅
=∞
⎢⎥
∆
⎣⎦
∫
∫
K
K
(12)
4.2 Spatial Domain
For all the outgoing directions of a given incident
direction, we represent the same-order Fourier
coefficients. If these coefficients have insensitive
angular dependencies on the outgoing directions, we
represent them directly using a linear combination of
spherical harmonics. Otherwise, we decompose
them into a smooth background and a sharp lobe.
Since the smooth background is dominated by the
low-frequency components, we can represent them
efficiently using a linear combination of low-level
spherical harmonics. The sharp lobe is dominated by
the high-frequency components, so we represent it
using a Gaussian. The decomposition is shown in
Figure 6. For the kth Fourier coefficients, the
representation is given as
,
,(, )
0
() (, ) (, , )
Ll
ilmo o kio o
klm
lml
AY G
θ
θϕ θθϕ
==−
+
∑∑
. (13)
Here the first term represents the smooth
background,
,
(, )
lm o o
Y
θ
ϕ
is the spherical harmonic
with the level (
l ,
m
),
L
the maximum level, and
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
410
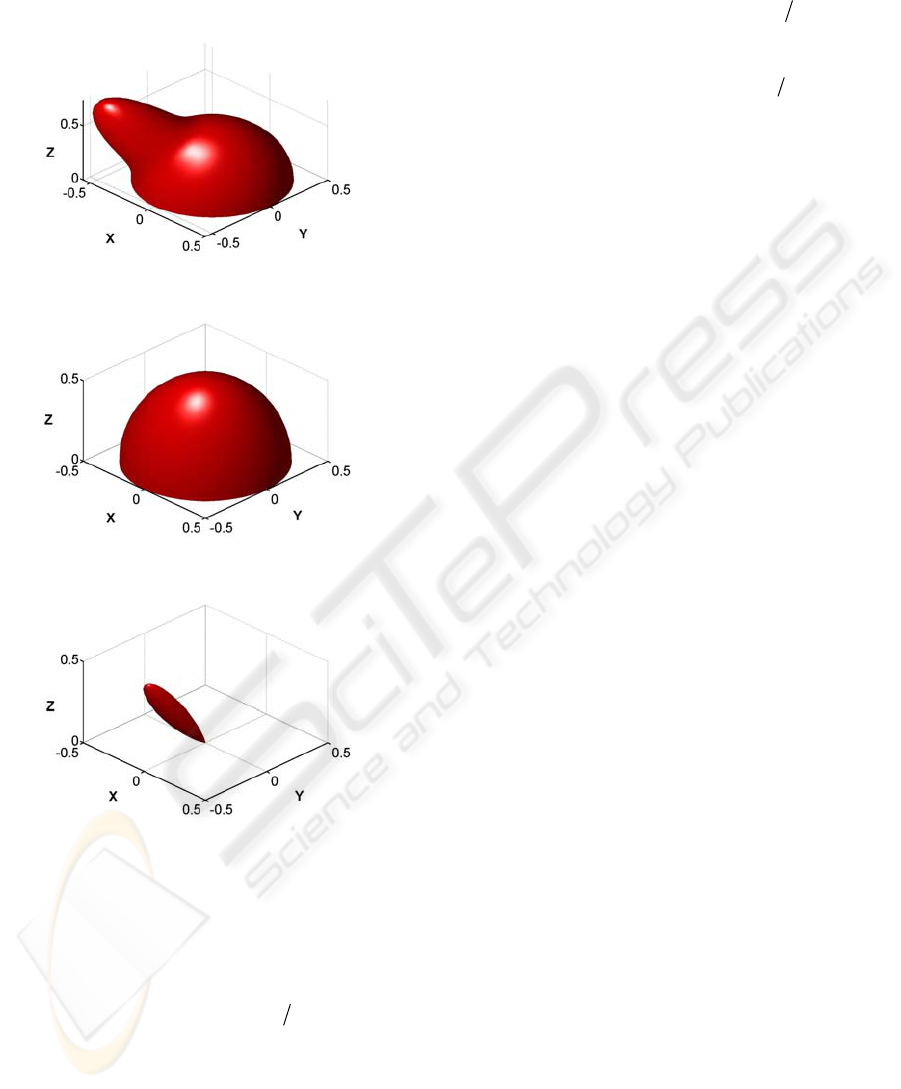
,(, )
()
i
klm
A
θ
the coefficients. The second term
(, , )
kioo
G
θ
θϕ
represents the sharp lobe, and it is a
Gaussian.
(a)
(b)
(c)
Figure 6: Decomposition of the same-order Fourier
coefficients (a) into a smooth background (b) and a sharp
lobe (c).
In this paper, we tried three Gaussians for the
representation of the sharp lobe. The first is given as
2
(, , ) exp[ (, , ) ]
kioo k kioo k
Gp b
θθϕ α θθϕ
=− , (14)
where
k
p
and
k
b specify the height and width of the
sharp lobe, and
(, , )
kioo
α
θθϕ
is the angle between the
outgoing direction
(, )
oo
θ
ϕ
and the direction of the
peak of sharp lobe. For the isotropic spectral BRDF,
the direction of the peak of sharp lobe is a function
of
i
θ
. The second is generated from the empirical
model (Ward, 1992)
2
( , , ) exp[ tan ( , , ) ]
kioo k kioo k
Gp b
θθϕ α θθϕ
=− , (15)
and the third from the physically based model (Sun,
2004)
( , , ) exp[ tan ( , , ) ]
kioo k kioo k
Gp b
θθϕ α θθ ϕ
=− . (16)
The decomposition of Fourier coefficients into a
smooth background and a sharp lobe is a key point
for this representation method. To achieve this, we
need to obtain the critical angle first. Then, for all
the outgoing directions with the angles from the
peak of the sharp lobe are larger than the critical
angle, we treat the Fourier coefficients as the smooth
background. We can use the regression analysis (or
linear least squares) to determine the coefficients
,(, )
()
i
klm
A
θ
. Finally, we extract the smooth
background from the Fourier coefficients, and use
the regression analysis (or linear least squares) to
determine the coefficients
k
p and
k
b .
Finding the critical angle is a little tricky since
we cannot directly obtain it from the raw data. In
this paper, we first evaluate the range of critical
angle from the raw data. Then we uniformly sample
the range with a reasonable interval. For each
sampled angle, we take it as the critical angle and
use it for the decomposition. Correspondently we
calculate the relative error between the raw data and
the representation. Finally we select the sampled
angle with the least relative error as the real critical
angle.
5 NUMERICAL STUDIES
In this paper, the raw data of spectral BRDF is
measured from a sample “ME01_AmberGlass”. The
data is non-uniformly sampled for the incident and
outgoing directions in terms of the geometry of
BRDF, and has the noises involved. Furthermore,
the data is sparsely distributed around some pairs of
incident and outgoing directions, while it is densely
distributed around some other directions.
5.1 Data Processing
Following Eqs. (5-10), we obtain the uniformly
sampled and noises-filtered spectral BRDF data. For
different incident angle
i
θ
, the spectral BRDF at
550nm
λ
=
for different outgoing directions is
shown in Figure 7. In this paper,
θ
φ
=−
stands for
the outgoing direction
(,0)
φ
° , and
θ
φ
= for
DATA PROCESSING AND COMPACT REPRESENTATION OF MEASURED ISOTROPIC SPECTRAL BRDF
411
( ,180 )
φ
° . We can see that the BRDF shows apparent
off-specular reflection for
15 ,45
i
θ
=° °. Moreover,
the BRDF shows higher peak for normal incidence,
and for the incidence close to the grazing direction.
0.00
0.20
0.40
0.60
0.80
1.00
1.20
1.40
-90-75-60-45-30-150 153045607590
Theta (degree)
BRDF
line 1
line 2
line 3
Figure 7: Spectral BRDF at
550nm
λ
=
for 0
i
θ
=° (line 1),
15
i
θ
=° (line 2), and 45
i
θ
=° (line 3).
Following Eq. (5), we interpolate the spectral
BRDF for the unmeasured pairs of incident and
outgoing directions. By converting the spectra into
the RGB color components, the BRDF for normal
incidence is shown in Figure 8.
0
5
10
15
20
25
30
0 102030405060708090
Theta (degree)
BRDF (RGB)
Figure 8: Interpolated BRDF for normal incidence.
From Figure 8, we can see some oscillations for
10 60
θ
°< < °. This phenomenon is commonly called
the ring effect. It may come from two reasons. One
is caused from the introduction of linear relations, as
shown in Eq. (10), and another from the inherit ring
effect of Eq. (5) (Glassner, 1995). To remove the
ring effect, we multiply a window function
(,,)wmnl
to the right term of Eq. (5),
1
23
(,,) cos[2( )]
cos[2( )]cos[2( )]
i
oo
wmnl mT
nT lT
θ
θϕ
=−
⋅− −
. (17)
In calculation, we always take
(,,) 0wmnl
=
if
(,,) 0wmnl
<
for some cases. The interpolated BRDF
with the ring effect removed is shown in Figure 9.
0
5
10
15
20
25
30
0 102030405060708090
Theta (degree)
BRDF (RGB)
Figure 9: Interpolated BRDF with the ring effect removed
for normal incidence.
5.2 Representation
The accuracy of a representation method can be
evaluated in terms of the relative error between the
reconstructed spectral BRDF and the original one
2
2
(, , ) (, , )
(, , )
oo
oo
reconstr i o o orig i o o
orig i o o
λθ ϕ
λθ ϕ
ρ θθϕ ρ θθϕ
η
ρθθϕ
⎡
⎤
−
⎣
⎦
=
⎡⎤
⎣⎦
∑∑∑
∑∑∑
,(18)
where
(, , )
reconstr i o o
ρ
θθϕ
and (, , )
orig i o o
ρ
θθϕ
are the
reconstructed and original spectral BRDFs,
respectively.
For the re-sampled and noises-filtered data, we
represent the spectral BRDF for each pair of incident
and outgoing directions with 19 Fourier coefficients,
while the original data size is 101. Since the spectral
BRDF is sensitively angular dependent, the same-
order Fourier coefficients of each sampled incident
direction is also highly angular dependent. We have
to decompose the Fourier coefficients into a smooth
background and a sharp lobe, and represent them
respectively. For normal incidence, Figure 9 shows
the comparisons between the original data and the
ones reconstructed from the representations at
550nm
λ
=
. Here, the line “orig” stands for the
original data, the line “rep 1” for the representation
using Eq. (14), the line “rep 2” for that using Eq.
(15), and the line “rep 3” for that using Eq. (16).
For
1
L
=
, as shown in Figure 9(a), the
representation error for the representation using
either Eq. (14) or Eq. (15) is 14.3%, and that using
Eq. (16) is 11.5%. From Figure 9(a), we can see that
the representation error mainly comes from the
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
412
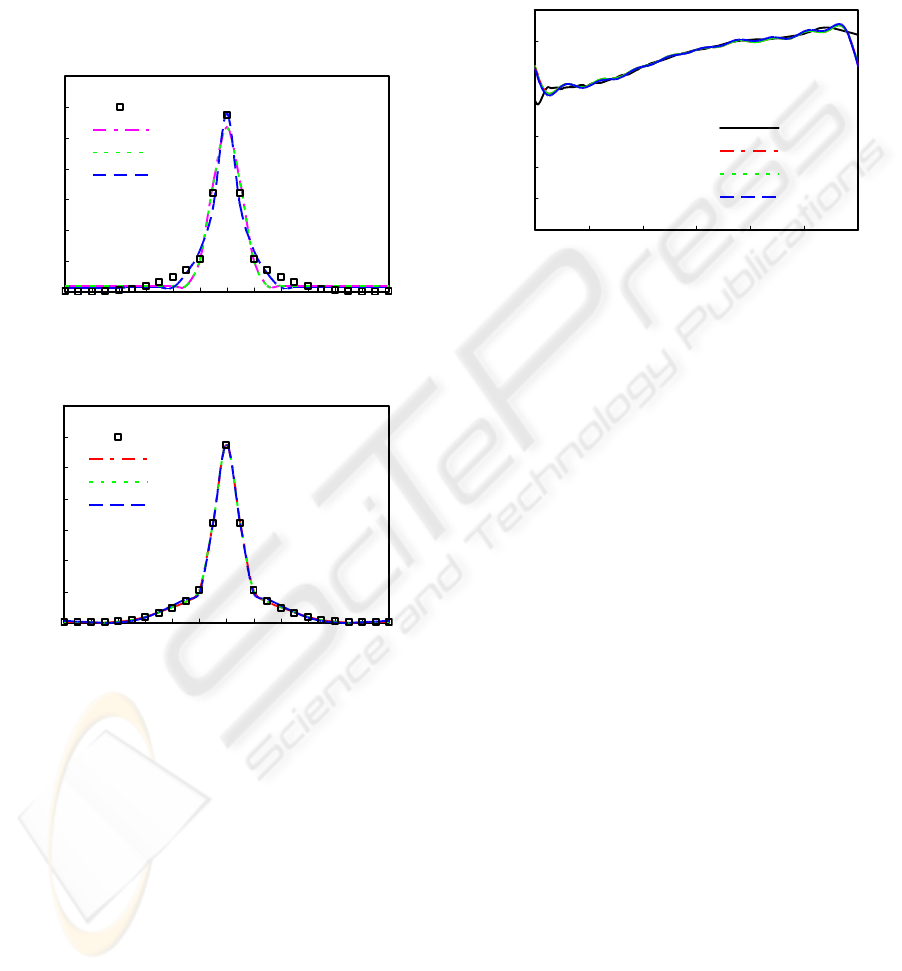
representation for the smooth background; this is
due to the fact that the low-level spherical harmonics
cannot represent the high-frequency components
completely. Moreover, we can see that the
representation using Eq. (16) matches the sharp lobe
of the original data better than the representations
using Eq. (14) and Eq. (15). This fact indicates that
the physical model (Sun, 2004) might match the
original data better than the empirical model (Ward,
1992).
0
0.2
0.4
0.6
0.8
1
1.2
1.4
-90 -75 -60 -45 -30 -15 0 15 30 45 60 75 90
Theta (degree)
BRDF
orig
rep 1
rep 2
rep 3
(a)
0
0.2
0.4
0.6
0.8
1
1.2
1.4
-90-75-60-45-30-150 153045607590
Theta (degree)
BRDF
orig
rep 1
rep 2
rep 3
(b)
Figure 10: Comparisons between the original data and the
representations for normal incidence.
For 4
L
= , as shown in Figure 9(b), the
representation error for using each of Eqs. (14-16) is
lower than 4.5%. Here, the total number of
coefficients used for representation is
(25 2) 19
+
× .
Consider the size of the original data size
13 49 101×× for each incident direction, in which the
sample interval for all the angles is
7.5 degrees, the
compression ratio is
125:1.
To understand how well the representations
match the original data for full range of wavelength,
we compare the original data with the
representations for the normal incidence and the
outgoing direction
(0 ,0 )°°, as shown in Figure 10.
We can see that the representation error mainly
comes from the two bottoms of full range of
wavelength. This is due to the property of Fourier
transformation; the representation always starts and
ends with the same value.
0
0.2
0.4
0.6
0.8
1
1.2
1.4
400 450 500 550 600 650 700
Wavelength (nm)
BRDF
orig
rep 1
rep 2
rep 3
Figure 11: Comparisons between the original data and the
representations for full range of wavelength.
6 CONCLUSIONS AND FURTHER
WORK
In this paper, we present the methods for both data
processing and compact representation of the
measured isotropic spectral BRDF. For the data
processing, we develop a numerical method to filter
the noises and resample the raw data by solving a
constrained linear least squares problem, and
interpolate the processed data for the unmeasured
pair of incident and outgoing directions from the
measured pairs. Numerical results show that the
interpolated spectral BRDF has the ring effect,
which might cause from the introduction of linear
relations into the matrix for linear least squares
analysis and the inherit ring effect. By introducing a
window function into the interpolation, the ring
effect is remarkably reduced.
For the compact representation of processed
data, we develop a method to represent the data in
both the spectral and spatial domains. In the spectral
domain, for each pair of the incident and outgoing
directions, we consider it as a spectrum, and
represent it with the Fourier coefficients by
performing the Fourier transformation to it. For all
the outgoing directions of a given direction, we
consider the same-order Fourier coefficients. If these
coefficients are insensitively angular dependent, we
represent them directly using a linear combination of
DATA PROCESSING AND COMPACT REPRESENTATION OF MEASURED ISOTROPIC SPECTRAL BRDF
413

spherical harmonics. Otherwise, we decompose
them into a smooth background and a sharp lobe; we
represent the smooth background using a linear
combination of spherical harmonics, and the sharp
lobe using a Gaussian. Numerical studies show that,
for the measured isotropic spectral BRDF of a
sample, the representation error can be lower than
4.5% by using
4
L
=
and the number of Fourier
coefficients 19. The compression ratio is achieved as
125:1.
In further work, we will continue to work on
representing the processed data for an arbitrary
incident direction. We will use both the processed
data and represented data for the spectral imaging
and give the comparisons. Furthermore, we will
measure the spectral BRDFs for different surfaces,
and use these methods for data processing and
representation. Once the data is processed, we will
compare it with the current analytic models for the
full range of wavelength, and find the hiding
problems with them. Based on the comparisons, we
can work on developing the new analytic models.
ACKNOWLEDGEMENTS
The author thanks Yinlong Sun for providing the
spectral BRDF of the sample “ME01_AmberGlass”.
REFERENCES
Beckmann, P., & Spizzichino, A., 1963, The scattering of
electromagnetic waves from rough surfaces
microform, Macmillan, New York.
Blinn, J. F., 1977, Models of light reflection for computer
synthesized pictures, Proc. Siggraph, pp. 192-198.
Carbral, B., Max, N., & Springmeyer, R., 1987,
Bidirectional reflection functions from surface bump
maps, Computer Graphics, vol. 21, no. 4, pp. 273-281.
Cook, R. L., & Torrance, K. E., 1982, A reflection model
for computer graphics, ACM Transactions on
Graphics, vol. 1, no. 1, pp. 7-24.
Dana, K. J., van Ginneken B., Nayar, S. K., &
Koenderink, J. J., 1999, Reflectance and texture of
real-world surfaces, ACM Transactions on Graphics,
vol. 18, no. 1, pp. 1-34.
DeYong, and Fourier A., 1997, Properties of tabulated bi-
directional reflectance distribution functions, Proc.
Graphics Interface, pp. 47-55.
Fournier, A., 1995, Separating reflection functions from
linear radiosity, Proc. Eurographics Workshop on
Rendering, pp. 296-305.
Glassner, A. S., 1995, Principles of Digital Image
Synthesis, Morgan Kaufmann Publishers, San
Francisco, CA.
He, X. D., Torrance, K. E., Sillion, F. X., and Greenberg,
D. P., 1991, A comprehensive physical model for light
reflection, Proc. Siggraph, pp. 175-186.
Koenderink, J. J., & van Doorn A. J., 1998,
Phenomenological description of bi-directional surface
reflection, J. Opt. Soc. Am. A., vol. 15, no. 11, pp.
2903-2912.
Lafortune, E. P. F., Foo, Sing-Choong, Torrance, K. E.,
Greenberg, D. P., 1997, Non-linear approximation of
reflectance functions, Proc. Siggraph, pp. 117-126.
Lawson, C. L., & Hanson, R. J., 1995, Solving Least
Squares Problems, Philadelphia: SIAM.
Marschner, S. R., Westin, S. H., Lafortune, E. P. F.,
Torrance, K. E., & Greenberg, D. P., 1999, Image-
based BRDF measurement including human skin,
Proc. Euro-graphics Workshop on Rendering, pp.
139-152.
Marschner, S. R., Westin, S. H., Lafortune, E. P. F., &
Torrance, K. E., 2000, Image-based measurement of
the bi-directional reflection distribution function,
Applied Optics, vol. 39, no. 16, pp. 2592-2600.
Murray-Coleman, J. F., & Smith, A. M., 1990, The
automated measurements of BRDFs and their
applications to luminaire modelling, Journal of the
Illumination Engineering Society, vol. 19, no. 1, pp.
87-89.
Phong, B., 1975, Illumination for computer generated
images, Communications of the ACM, vol. 18, no. 6,
pp. 311-317.
Schröder, P., & Sweldens, W., 1995, Spherical wavelets:
efficiently representing functions on the sphere,
Computer Graphics, vol. 29, pp. 161-172.
Sillion, F. X., Arvo, J. R., Westin, S.H., and Greenberg, D.
P., 1991, A global illumination solution for general
reflectance distributions, Computer Graphics, vol. 25,
no. 4, pp. 187-196.
Strauss, P., 1990, A realistic lighting model for computer
animators, IEEE Computer Graphics & Appl., vol. 10,
no. 6, pp. 56-64.
Sun, Y., 2004, Self shadowing and local illumination of
randomly rough surfaces, Proc. CVPR, pp. 158-165.
Sun, Y., & Wang, Q., 2005, Spectral BRDF measurement
and data interpolation, Proc. of the 13th Color
Imaging Conference, pp. 114-119.
Torrance, K. E., & Sparrow, E. M., 1967, Theory for off-
specular reflection from roughened surfaces, J. Opt.
Soc. Am., vol. 57, no. 9, pp. 1105-1114.
Ward, G. J., 1992, Measuring and modelling anisotropic
reflection, Proc. Siggraph, pp. 265-272.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
414
