
EFFICIENT RENDERING OF HIGH-DETAILED OBJECTS USING A
REDUCED MULTI-RESOLUTION HIERARCHY
Mathias Holst
University of Rostock
Albert-Einstein-Str. 21, 18059 Rostock, Germany
Heidrun Schumann
University of Rostock
Albert-Einstein-Str. 21, 18059 Rostock, Germany
Keywords:
Multi-Resolution Modeling, Real-Time Rendering.
Abstract:
In the field of view-dependant continuous level of detail of triangle-meshes it is often necessary to extract
the current LOD triangle by triangle. Thus, triangle strips are only of very limited use, or only usable with a
high effort. In this work a method is proposed that allows a stepwise reduction of a great, fine stepped LOD
hierarchy by merging nodes. The result of this process is a reduced hierarchy, which allows the extraction of
many neighboring static triangles in one step, so that triangle strips are applicable more efficiently. We show
that this results in a significant decimation of processed vertices without loosing a smooth LOD transition.
1 INTRODUCTION
It is not possible to render high-detailed triangle
meshes with interactive framerates even with current
hardware. In many cases the triangle size in image
space is very low (< 1 pixel) and it is often more nec-
essary to achieve interactive framerates than showing
fine details. Thus, level of detail techniques are an
important part of many rendering techniques for large
scenes and high-detailed objects. For this purpose,
the original triangle mesh is simplified using global
or local operations (see (Luebke et al., 2002) for an
overwiew). Every operation creates a level of detail
(short LOD) of the original mesh. During rendering a
certain LOD is selected with respect to a high image
quality versus low costs.
For doing so, there are two techniques: Discrete
techniques save a certain number of offline generated
LOD. Then, in every frame, an appropriate LOD is se-
lected, e.g. depending on the viewer distance. On the
other hand, continuous techniques use a data struc-
ture to extract an appropriate LOD, which contains
the whole detail spectra of the original mesh. The
advantage of continuous techniques is a very smooth
LOD transition in contrast to discrete approaches, and
they adapt the LOD better to the viewing situation, so
that in most cases less triangles have to be rendered
compared to using a discrete LOD.
On the other side graphics cards are specialized to
accelerate the rendering of large triangles sets, e.g.
using triangle strips. A triangle strip is a sequence of
triangles in which adjacent triangles share a common
edge. A strip of k triangles is described as a sequence
of k +2vertices: three vertices for the first triangle
and one for each additional triangle. A set of triangle
strips that contains all triangles of a mesh is called a
striptification of that mesh.
Triangle strips are very useful when using discrete
LOD techniques, because the whole LOD is rendered
at once. In contrast, triangle strips are less useful
when using continuous techniques. This is because
triangles, that belong to LOD are extracted in small
sets only. Thus, the triangle strip length is limited to
this set size. To overcome this limitation more sophis-
ticated and time consuming striptification techniques
have to be used. Thus, sometimes discrete LOD tech-
niques are more efficient than continuous LOD, al-
though discrete LOD contain more triangles (but less
vertices because of longer triangle strips).
To decrease the number of processed vertices in
continuous LOD by using triangle strips, a trade-off
has to be found: On the one hand the calculation effort
should be small (time-consuming calculations should
be done offline), and triangle strips should be as long
as possible on the other hand.
In this paper a continuous technique is proposed
that uses triangle strips more efficiently. Thus, the
rendering process is accelerated significantly. A LOD
is created by small patches in our approach. Every
patch contains a small amount of adjacent triangles.
3
Holst M. and Schumann H. (2006).
EFFICIENT RENDERING OF HIGH-DETAILED OBJECTS USING A REDUCED MULTI-RESOLUTION HIERARCHY.
In Proceedings of the First International Conference on Computer Graphics Theory and Applications, pages 3-10
DOI: 10.5220/0001351100030010
Copyright
c
SciTePress

Such a patch is described by a few triangle strips. We
have developed a technique to enlarge these patches
offline before rendering, so that longer triangle strips
are useable. In contrast to other approaches these tri-
angle strips are static, so that the striptification is com-
puted offline, too. This results in a fast LOD extrac-
tion during rendering time.
The remainder of this paper is structured as fol-
lows. First, in section 2, we will give a short overview
on related works. Section 3 describes the basic LOD
structure we use. In section 4 we demonstrate, how
the patch size is increased by reducing this structure.
After this, we will discuss the achieved results in sec-
tion 5. We conclude with a short summary and an
outlook to future work in section 6.
2 RELATED WORK
The rendering acceleration of continuous LOD
meshes by using triangle strips was the issue of some
previous works. The Skip Strip algorithm (El-Sana
et al., 1999) uses a merge tree that is represented by
a skip strip. For the original mesh a striptification is
created, which is updated and repaired during traver-
sal the strip. In addition, the generated triangle strips
are scanned for redundant vertices before rendering.
In (Stewart, 2001) an elegant and efficient algo-
rithm for creating a striptifaction of a static mesh is
proposed using a so called tunneling-operator. This
operator connects previously given triangle strips it-
eratively to reduce their number. They show how
this operator can be used to update a striptification
that was broken by a local vertex-split (resp. edge-
collapse) operation. Thus, it can be used for continu-
ous LOD, too.
In (Velho et al., 1999) an initial striptification is
generated for a low detailed mesh. After this, the
mesh is refined by inserting new vertices and edges,
so that the resulting new triangles can be inserted in
the initial striptification, without requiring more trian-
gle strips. The position of an inserted vertex is esti-
mated from an implicit or parametric surface descrip-
tion.
All these techniques do not limit the length of tri-
angle strips. On the other side triangle strips are not
static and have to be updated from LOD to LOD, so
potentially in every frame. This is time consuming,
especially the LOD changes a lot. In our approach
the triangle strip length is limited, but they are static,
and can be generated offline. Since the benefit of tri-
angle strips decreases with their length, the overhead
for processed vertices is small (as shown in section
5). In addition the whole striptification can be stored
in a vertex buffer on the graphics card to further re-
duce the rendering time. This is not possible using
dynamic triangle strips, as are used in the described
approaches.
Beside these works, there are algorithms that focus
on special object types, unlike our approach, which
can be used for nearly all kind of objects: In (Lind-
strom et al., 1996) an efficient algorithm for height
fields is proposed. The single LOD of these land-
scapes are represented by Quad-Trees. The ROAM-
Renderer (Duchaineau et al., 1997) was developed for
landscapes, as well. It includes an iterative algorithm
to get and update triangle strips with a length of four
or five triangles. Both approaches also create trian-
gle strips during or after LOD selection, unlike our
approach, which uses static triangle strips.
3 BASIC LOD HIERARCHY
To render an original mesh regarding the viewing dis-
tance and other parameters, a data structure is needed
that allows the access to all surface areas in differ-
ent resolutions. These structures are in general hier-
archies or trees, like the merge tree (Xia et al., 1997).
We use the elegant MT-hierarchy developed in (Flo-
riani et al., 1997). Using this, it is already possible
to extract a small patch of two or more fixed trian-
gles that belong to a certain LOD at once. This is an
important property as shown in section 4.
The MT-hierarchy is a directed acyclic graph (ab-
breviated DAG) G =(N , A). Its nodes N repre-
sent local simplification operation and are labeled by
a simplification error. Hierarchy arcs
1
are labeled by
triangle sets. We denote a triangle set of an arc a as
a patch p
a
. The outgoing arcs of a node contain all
triangles that are changed (or deleted) by this simpli-
fication operation, and its ingoing arcs contain these
changed triangles (figure 1). There are two special
nodes: The drain node n
D
at the bottom of the hi-
erarchy (with simplification error 0), whose ingoing
arcs represents the original mesh, and the source node
n
S
on top of the hierarchy (with simplification error
∞), whose outgoing arcs contains the most simplified
mesh.
3.1 Hierarchy Creation
The hierarchy is generated bottom up, as described
in (Floriani et al., 1997). We use edge-collapse op-
erations (Hoppe et al., 1993) to simplify the original
mesh iteratively: All possible edge-collapse opera-
tions are ordered in a priority queue, in respect to their
simplification error. This queue is processed until it
1
Since we operate on meshes, the term ”edge” already
has a meaning. For clarity the term ”arc” is used for a hier-
archy edge.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
4
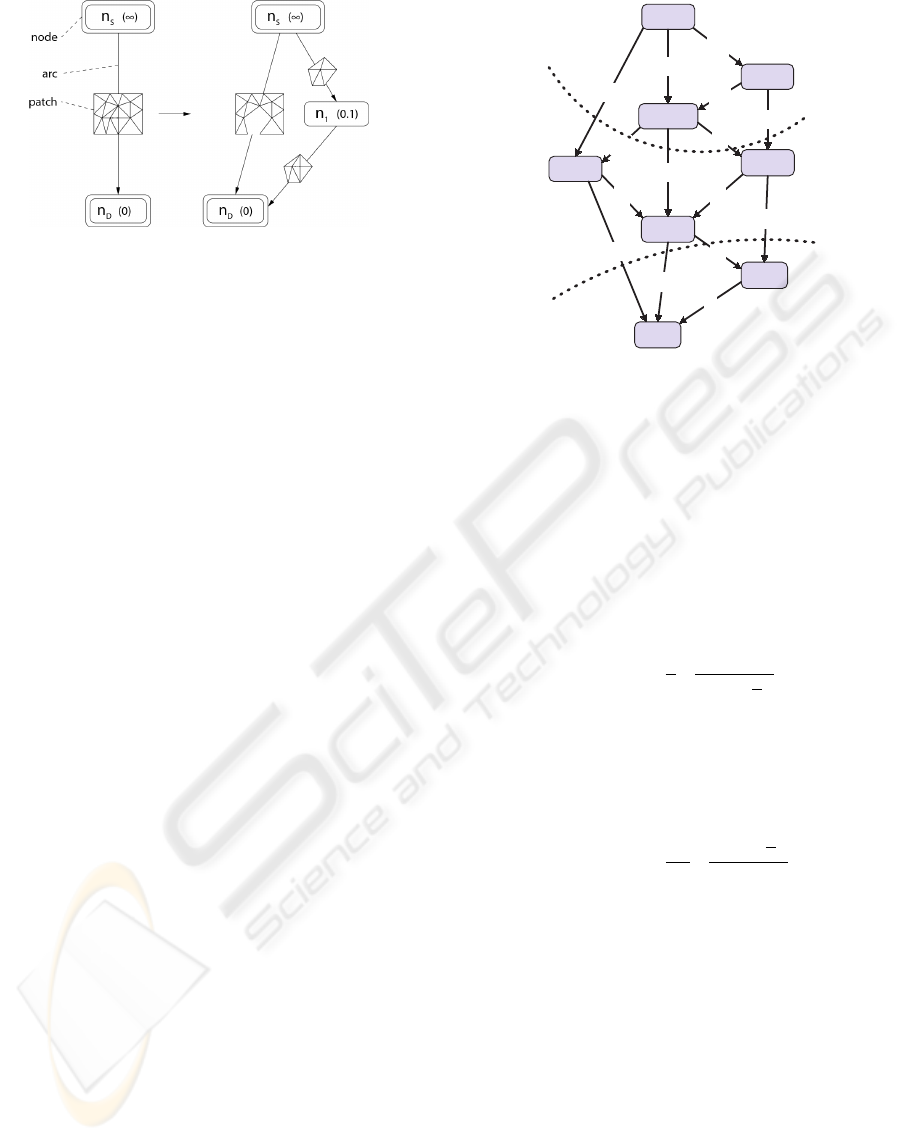
(a) (b)
Figure 1: Hierarchy creation steps: basic mesh, the dashed
edge is collapsed (a), patch hierarchy after this edge-
collapse operation with simplification error 0.1 (b).
is empty. We calculate the simplification error using
the widely used quadric error metric (short: QEM)
(Garland and Heckbert, 1997). By this iterative cre-
ation and by the QEM it is ensured that the simplifi-
cation error of the father node n
i
of every arc (n
i
,n
j
)
is greater than (or equal to) the simplification error of
its child node n
j
.
3.2 LOD Selection
To extract a LOD out of the hierarchy it is necessary
to create a cut. A cut is an arc subset C⊆Awith the
following two properties:
1. ∀ a=(n
i
,n
j
),a
=(n
k
,n
l
) ∈C: ∃ n
j
→
∗
n
k
(→
∗
denotes a path of any length)
2. C is maximal (no arc can be added to C without
breaking property 1).
The first property ensures that there are no overlap-
ping arc patches. The second property ensures on the
other hand, that the whole original mesh is covered by
the arc patches of the cut.
Since the simplification error e
i
, that is stored in
every node n
i
, decreases monotonically from top to
bottom of the hierarchy, a cut is uniquely defined by:
C = {(n
i
,n
j
) ∈ A : e
i
≥ ε>e
j
} (1)
as shown in figure 2. The parameter ε describes the
desired LOD accuracy. A simple algorithm scans A
linearly for cut determination. Since the hierarchy has
a logarithmic height, it is of course more efficient to
traverse the hierarchy bottom up or top down to avoid
unnecessary arc tests. Usually a cut does not change
very much from frame to frame. Thus, it is even better
to update the cut of the last frame up or down to get
the cut for the current frame as described in (Floriani
et al., 1998).
Since the QEM measures a quadratic distance in
object space, ε has to be interpreted as a quadratic
n
3
(0.2)
n
2
(0.1)
a
5
n
5
(0.3)
n
1
(0)
n
D
(0)
a
8
a
11
a
2
a
1
a
3
a
4
a
9
n
6
(0.5)
a
12
n
4
(0.2)
n
S
(
∞
)
a
6
a
10
a
13
a
14
a
15
a
7
cut 1
cut 2
Figure 2: Demonstration of two cuts specifying differ-
ent LOD. The first cut C
1
= {a
8
,a
9
,a
10
,a
11
,a
13
} for
ε =0.25 and the second cut C
2
= {a
2
,a
3
,a
4
,a
6
} for
ε =0.05.
distance, too. However, using an image error in pixels
is more intuitive. Thus, we propose to define ε by
a pixel value γ in image space: Using a perspective
projection the length l of a line defined in object space
with a distance d to the viewer has the maximum pixel
length s in image space of
s(l, d)=
l
d
·
h
2 tan
α
2
, (2)
where h is the output image height (in pixels) and α
is the field of view angle.
If the user defines an image error γ in pixels, then
its quadratic length in object space is given by
ε =(s(l, d
O
)
−1
)
2
=
d
O
γ
·
2 tan
α
2
h
2
, (3)
where d
O
is the object distance to the viewer. Using
the bounding sphere of the object with center M
O
and
radius r
O
, the value of d
O
is bounded below by
d
O
= max(|M
O
− V |−r
O
, 0), (4)
where V is the viewer position in object space. If γ,
d
O
, the image dimension h or the field of view angle
α change, ε is recalculated and a new cut is deter-
mined.
In figure 3 examples for different choices of γ and
their effect on image quality are shown.
This cut estimation only considers the object dis-
tance to the viewer. But it is of course extensible by
using a more sophisticated cost and benefit heuristic
as proposed in (Funkhouser and Sequin, 1993).
EFFICIENT RENDERING OF HIGH-DETAILED OBJECTS USING A REDUCED MULTI-RESOLUTION
HIERARCHY
5
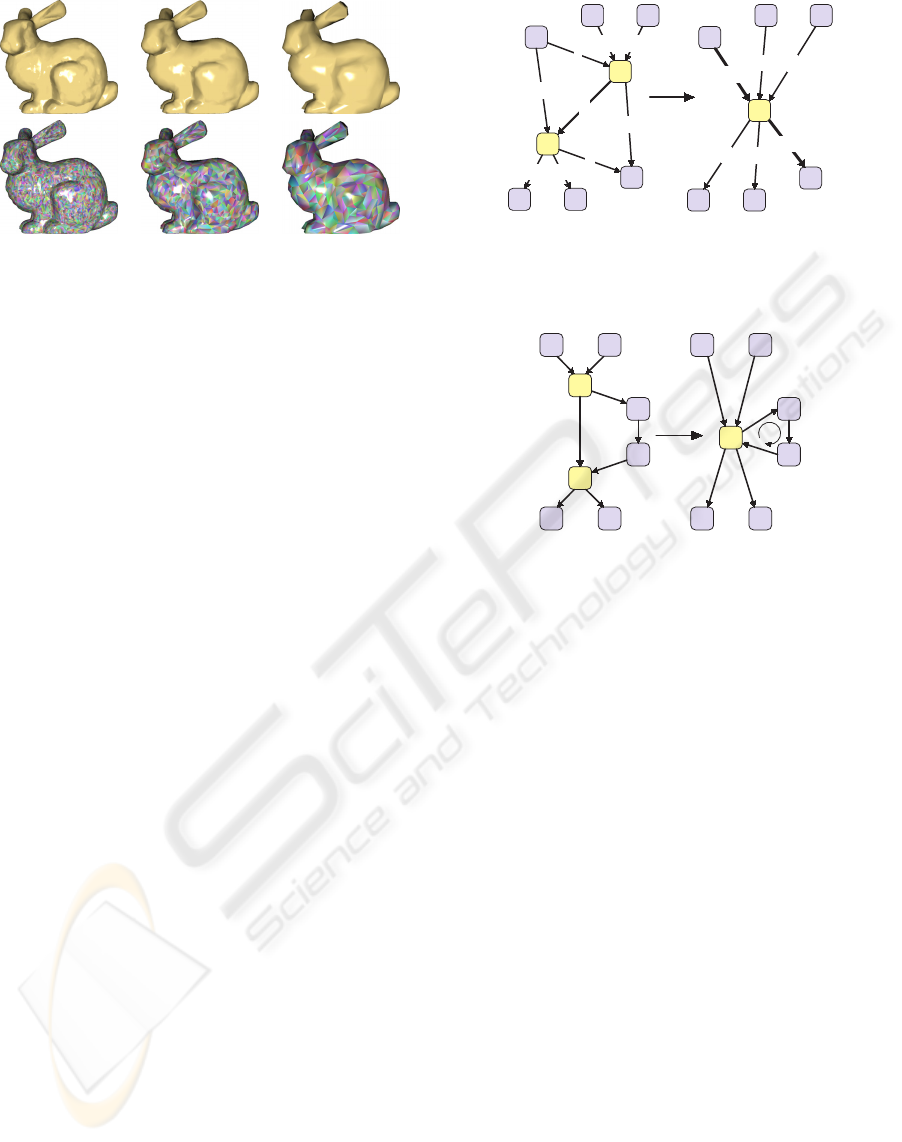
(a) γ =1 (b) γ =5 (c) γ =20
13k vertices 4k vertices 1.8k vertices
Figure 3: Showing LOD selection using the Stanford
bunny: With increasing allowed pixel error the granular-
ity of the mesh decreases significantly for the benefit of less
vertices.
4 PATCH ENLARGEMENT
Our purpose is to accelerate rendering by using trian-
gle strips, because the number of processed vertices
is a frame rate limiting factor. Since we construct a
certain LOD out of several patches, triangle strips can
only be defined within these patches. But an arc patch
of the hierarchy contains only ≈ 2 triangles in aver-
age, so triangle strips are not very efficient. Thus, it is
useful to enlarge these patches.
4.1 Arc-Collapse Operator
To achieve a larger average patch size, a coarser local
simplification operations than the common used edge-
collapse operator could be used, e.g. the removal of
more than one vertex at once, with a following retri-
angulation of the created mesh hole. But it is hard to
archive a specified average patch size using this ap-
proach. In addition other operators have to be used
(and implemented), if a different patch size is desired.
Thus, we propose another way: To increase the aver-
age patch size we introduce an arc-collapse opera-
tor, which merges two adjacent hierarchy nodes. This
has the effect that the ingoing arcs (resp. outgoing
arcs) of both merged nodes with the same father node
(resp. child node) are merged to one arc each (figure
4). Thus, larger patches are created. This arc col-
lapsing can be interpreted as the application of two
simplification operations at once instead of one after
the other.
To guarantee that the used hierarchy is still a DAG
after an arc-collapse operation, it has to be ensured
that there is no other path between the merged nodes
than this arc, otherwise a cycle is created (figure 5).
This would cause a conflict situation during cut esti-
mation.
n
î
n
j
a
c
n
a
n
b
n
c
n
f
n
e
n
d
a
k
a
m
a
n
a
o
a
p
a
r
a
s
a
l
n
i
n
a
n
b
n
c
n
f
n
e
n
d
a
m
a
n
a
o
a
p
(a
r,
a
s
)
(a
k,
a
l
)
collapse
Figure 4: Arc collapse operation: If arc a
c
=(n
i
,n
j
) is
collapsed to a new node other arcs a
k
,a
l
and a
r
,a
s
are
merged to new arcs, that contain larger patches.
n
î
n
j
n
a
n
b
n
c
n
f
n
e
n
d
n
î
n
a
n
b
n
c
n
f
n
e
n
d
collapse
Figure 5: Error situation: If there is another path between
two nodes of an arc, this arc can not be collapsed, because
a cycle would be created.
A collapse of randomly selected arcs is not pur-
poseful, because several criteria should be consid-
ered: On the one hand a desired average patch size
should be achieved by collapsing as few arcs as possi-
ble. On the other hand an efficient striptifaction of the
resulting patches and the keeping of a smooth LOD
transition are important.
For achieving an average patch size two factors are
relevant.
1. The number of triangles in the patch p
a
of the col-
lapsed arc a, denoted as |p
a
|:If|p
a
| is small the
average patch size is bigger after collapsing this arc
than if |p
a
| would be greater. Hence, a small |p
a
|
should be preferred.
2. The patch sizes of merged arcs: M
a
denotes the
set of the merged arc pairs (in figure 4: M
a
=
{(a
k
,a
l
), (a
r
,a
s
)}). Using this, the sum ps of the
patch sizes is estimated by:
ps(a)=
(a
,a
)∈M
a
|p
a
| + |p
a
| (5)
If ps is big, few large, or many small patches are
created, which yields a bigger average patch num-
ber as wanted. On the other side, it is better to
merge as many small patches as possible in order
to get a nearly constant patch size over the whole
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
6

(a) original (b) av. patch size 5 (c) av. patch size 10 (d) av. patch size 20
7512 patches 3575 patches 1941 patches 1018 patches
Figure 6: Rendering of the same LOD of the Armadillo model with different average patch sizes (each patch is differently
colored).
hierarchy, because patches can only be enlarged.
Thus, it is useful to use ps in relation to the number
of merged arcs:
ps
rel
(a)=
ps(a)
|M
a
|
. (6)
It sometimes happens that merging two arcs in M
a
does not form a contiguous patch. Thus, for these
patches at least 2 triangle strips have to be used,
so that there would be no benefit in the number of
processed vertices. Denotes U
a
⊆M
a
the set of arc-
pairs with neighboring patches:
U
a
={(a
,a
) ∈M
a
: p
a
,p
a
neighboring}, (7)
then a relation adj that considers this is given by:
adj(a)=
|U
a
|
|M
a
|
(8)
and should be considered for selecting an arc to col-
lapse, whereas adj should be as large as possible.
To preserve a smooth LOD transition inside the hi-
erarchy as far as possible, the relation e
diff
of the
simplification errors of a collapsed arc’s father node
and child node is considered. If it is small, a smooth
LOD transition is preserved after collapsing this arc.
The value e
diff
for every a =(n
i
,n
j
) is given by:
e
diff
(a)=
max(e
i
,µ)
max(e
j
,µ)
, (9)
where µ is a very small constant. This constant is nec-
essary because e
j
can be 0 (e.g. if n
j
is the drain node
n
D
). Thus, e
diff
= ∞, which would have the effect
that such edges would not be collapsed, although a
smooth LOD transition could be given. Our choice
for µ is the smallest simplification error =0of all
nodes in N divided by 10, which seems to be a prac-
ticable value.
To use all these factors for creating an order of arc
collapse operations, it is useful to combine them to
a single weight w(a) for every arc a. We found that
it is very effective to multiply these factors (or their
reciprocal) equally weighted, so that a small weight
means to collapse an arc before higher weighted arcs.
w(a)=|p
a
|·e
diff
(a) · ps
rel
(a) ·
1
adj(a)
. (10)
To achieve a specific average patch size our proce-
dure is as follows: All arcs are ordered in a priority
queue, starting with the smallest weight. Then, itera-
tively, the arc at the head of this queue is collapsed (if
it does not produce a cycle, of course). During this,
weights of the in- and outgoing arcs of the merged
nodes are updated. We stop collapsing arcs if the de-
sired average patch size is reached (or if there is only
one arc left in the hierarchy).
Results of such a hierarchy reduction by using arc-
collapse operations are shown in figure 6: The num-
ber of patches gets significantly smaller with bigger
patch sizes.
4.2 Node Error Adjustment
As illustrated in figure 7(a) the simplification error of
an arc’s father node can get smaller than its child node
after an arc-collapse operation. Thus, the LOD se-
lection algorithm (3.2) is non-deterministic. To solve
this problem the hierarchy is repaired by an additional
breadth-first traversal after reduction. This traversal
detects these problematic arcs. If such an arc is found
the simplification error of its father node is set to its
child’s simplification error (figure 7(b)). This slightly
decreases the LOD selection precision. Thus, a higher
LOD is selected than necessary, which reduces exigu-
ously the efficiency of the reduced hierarchy.
EFFICIENT RENDERING OF HIGH-DETAILED OBJECTS USING A REDUCED MULTI-RESOLUTION
HIERARCHY
7
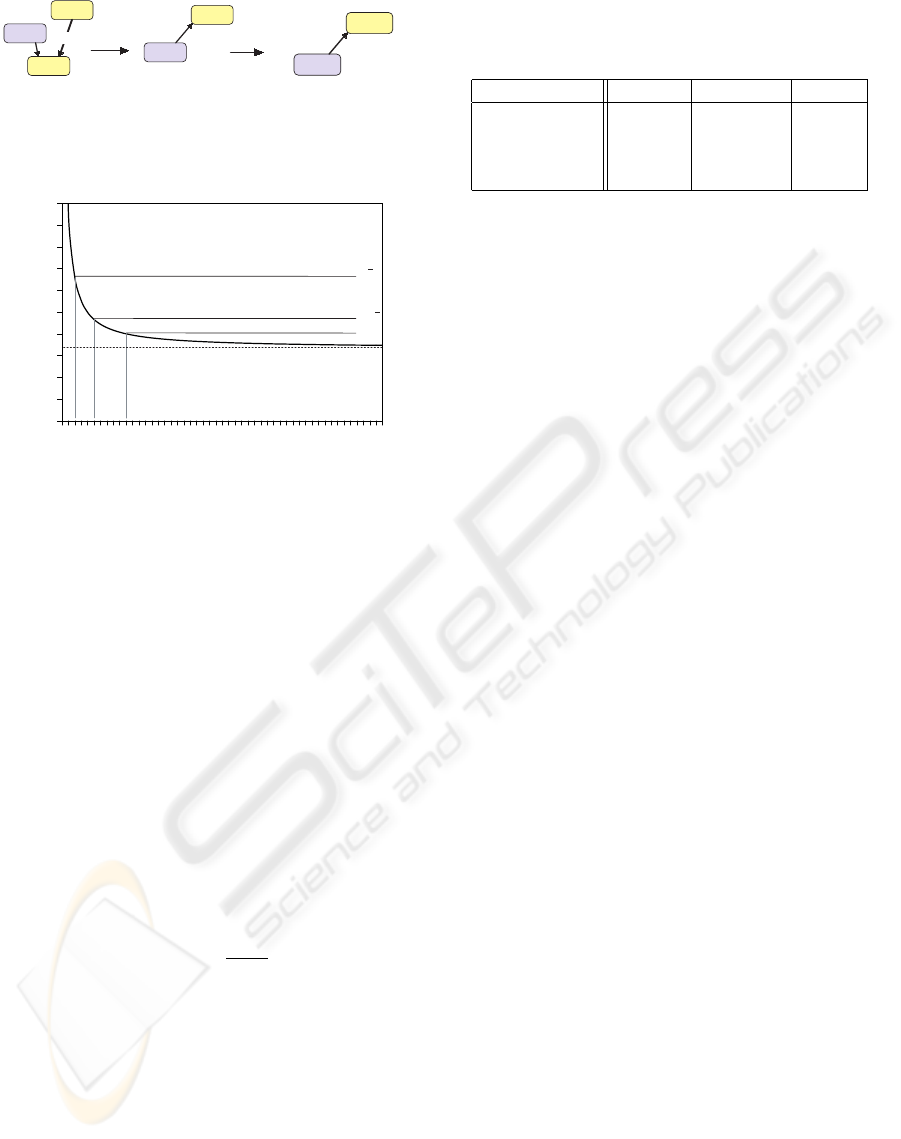
n
c
(0.1)
n
a
(0.2)
n
b
(0.3)
a
collapse
n
a
(0.2)
n
b
(0.3)
scan
n
a
(0.3)
n
b
(0.3)
(a) (b)
Figure 7: After collapsing arc a the monotonic bottom-up
increase of simplification errors is broken.
0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
1
05540453035202510150
t
s
ts
(t)
6.0
64.0
4.0
Figure 8: Efficiency of triangle strips in comparison to ren-
der each triangle of the strip separately.
5 DISCUSSION AND RESULTS
After introducing a possible way to achieve a certain
average patch size easily, in this section we will dis-
cuss, what patch size is appropriate for what purpose.
In addition the efficiency of our approach is shown,
especially in comparison to discrete LOD.
5.1 Appropriate Patch Sizes
To answer the question what average patch size pro-
vides most benefits, we first look at the saving factor
that triangle strips provide. This is the number of ver-
tices of a strip in relation to the number of triangle
vertices:
s
ts
(t)=
2+t
3t
, (11)
where t is the number of triangles. As you can see
in figure 8, the benefit of triangle strips converges to
1/3 very fast with increasing triangle number. Using
the original hierarchy with an average patch size of 2
you can save ≈ 33% vertices by using triangle strips
(assuming that every patch is represented by only one
strip). If the patch size is increased to 10, an addi-
tional 27% is saved, which is only 6.
¯
6% above the the-
oretical minimum. That this benefit is nearly reached
can be seen in figure 9(a), which shows the number of
processed vertices for our Armadillo model at differ-
ent LOD for some different average patch sizes, and
Table 1: Number of arcs and needed vertex-buffer mem-
ory using hierarchies for the Armadillo model with different
patch sizes.
patch size #arcs vb size saving
original (≈2) 722076 147.8MB −
5 258504 99.1MB 32.9%
10 118403 84.5MB 42.8%
20 55612 76.5MB 48.2%
in figure 9(b), which shows the vertex number in rela-
tion to the original hierarchy. In some cases the results
are not exactly as good as expected. This is because
for some large patches more than one triangle strip is
needed.
It can also be seen in figure 9(b) that the results for
using bigger patch sizes are always better than using
the original hierarchy, which shows that the patch size
is very uniform over the whole reduced hierarchy. It is
also easy to see in figure 9(b) that the relation varies
significantly on low LOD using bigger patch sizes.
This is because the LOD transitions get coarser with
higher distances too, and the LOD do not adapt to user
distance as well as when using the original hierarchy.
Another positive effect of reducing the hierarchy is
that by collapsing arcs, the patches of these arcs are
deleted, too. Thus, the number of vertices that are
held in memory is reduced additionally. As shown in
table 1 the number of arcs in a hierarchy with an aver-
age patch size of 20 is 13 times less than the number
in the original hierarchy. If the triangle strip vertices
of all patches are stored in one vertex buffer, using
three attributes each (position, normal and color), for
the Armadillo model you need 147.8MB using the
original hierarchy. If the hierarchy of patch size 20
is used, this is reduced by over 48%. In addition, the
cut estimation (as shown in section 3.2) is even faster,
because less arcs have to be checked, whether they
belong to cut or not.
We can conclude that if a fine LOD transition is
important, an average patch size of 5 − 10 is a good
choice. If the memory requirements of the vertex
buffer is more important, e.g. it should fit in the very
limited graphics card memory, a value over 10 should
be used instead. Hence, an average patch size of 10
is a good compromise between a fine LOD transition,
vertex number and memory requirements.
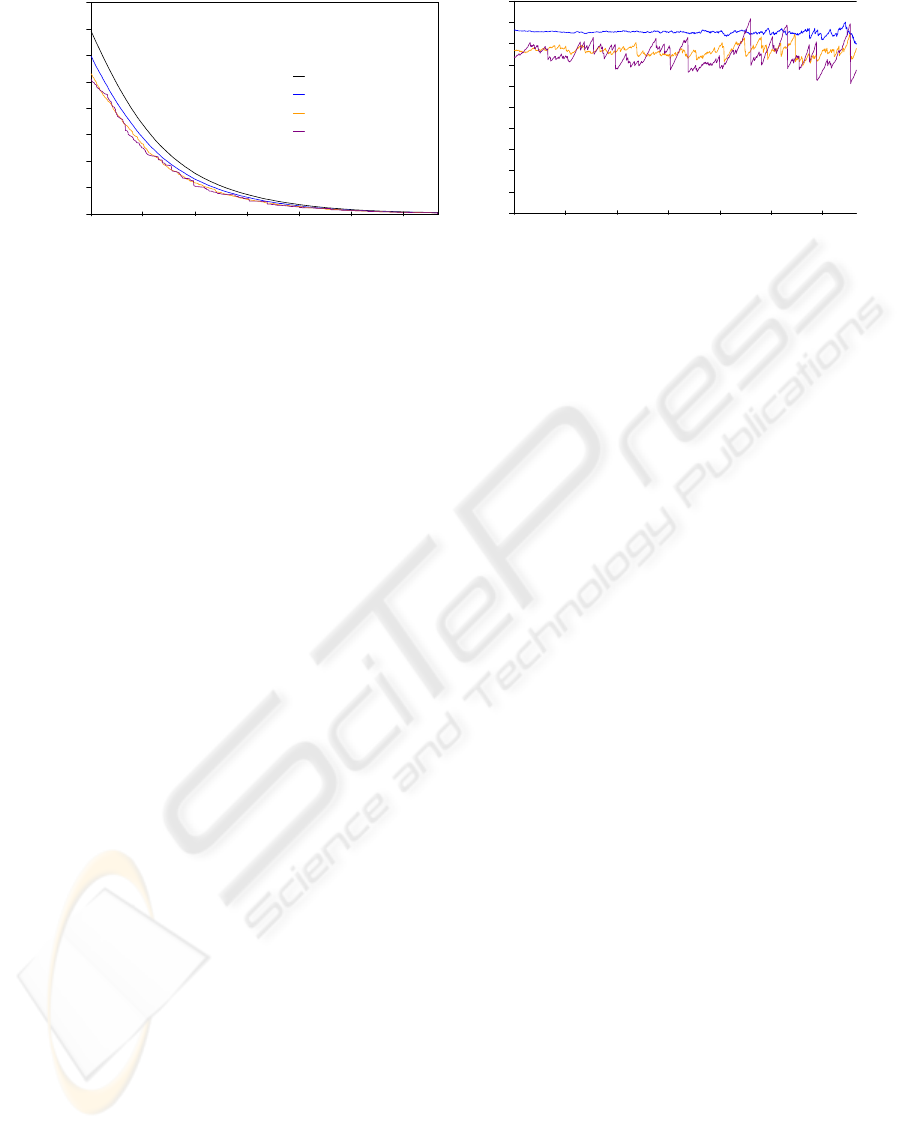
5.2 Patch Striptification
The used triangle strip algorithm has a big influence
on our approach. We use the tunneling-algorithm
(Stewart, 2001), because it always reaches better re-
sults than the classical SGI algorithm (Akeley et al.,
1990) or the STRIPE algorithm (Evans et al., 1996).
Using this we reach an average triangle strip number
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
8
0
00005
000001
000051
000002
000052
000003
000053
000004
4623618421
)elacs cimhtiragol( ecnatsid
vertices
yhcrareih lanigiro
5 ezis hctap
01 ezis hctap
02 ezis hctap
0
1.0
2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
1
4623618421
)elacs cimhtiragol( ecnatsid
relative to original
(a) (b)
Figure 9: Number of triangle strip vertices of different LOD at different distances using different patch sizes (a) and these
numbers of vertices in relation to to the original hierarchy (b).
per patch of less than 2 even when using a patch size
of 50.
5.3 Comparison to discrete LOD
A discrete LOD transition has several benefits com-
pared to a continuous LOD, because the whole LOD
mesh is given explicitly. Thus, no LOD extraction
is necessary. In addition the whole LOD mesh can
be striptified. Thus, the triangle strip length is not
limited, which generally results in less triangle strips,
unlike in our approach. Hence, also fewer vertices
are used to render the LOD. As shown in section 5.1
and figure 8, the theoretical maximum of this vertex
decimation is over 33% compared to the original hi-
erarchy with a patch size of 2. But if an average patch
size of 10 is used, this decimation is only about 7% .In
addition a discrete LOD algorithm does not produce a
smooth LOD transition.
We compared our approach with a discrete LOD
mechanism. To do so, we created a cut using the
original hierarchy for every distance with a positive
integer power of 2, and used these cuts to create dis-
crete LOD. Every discrete LOD got a validity up to
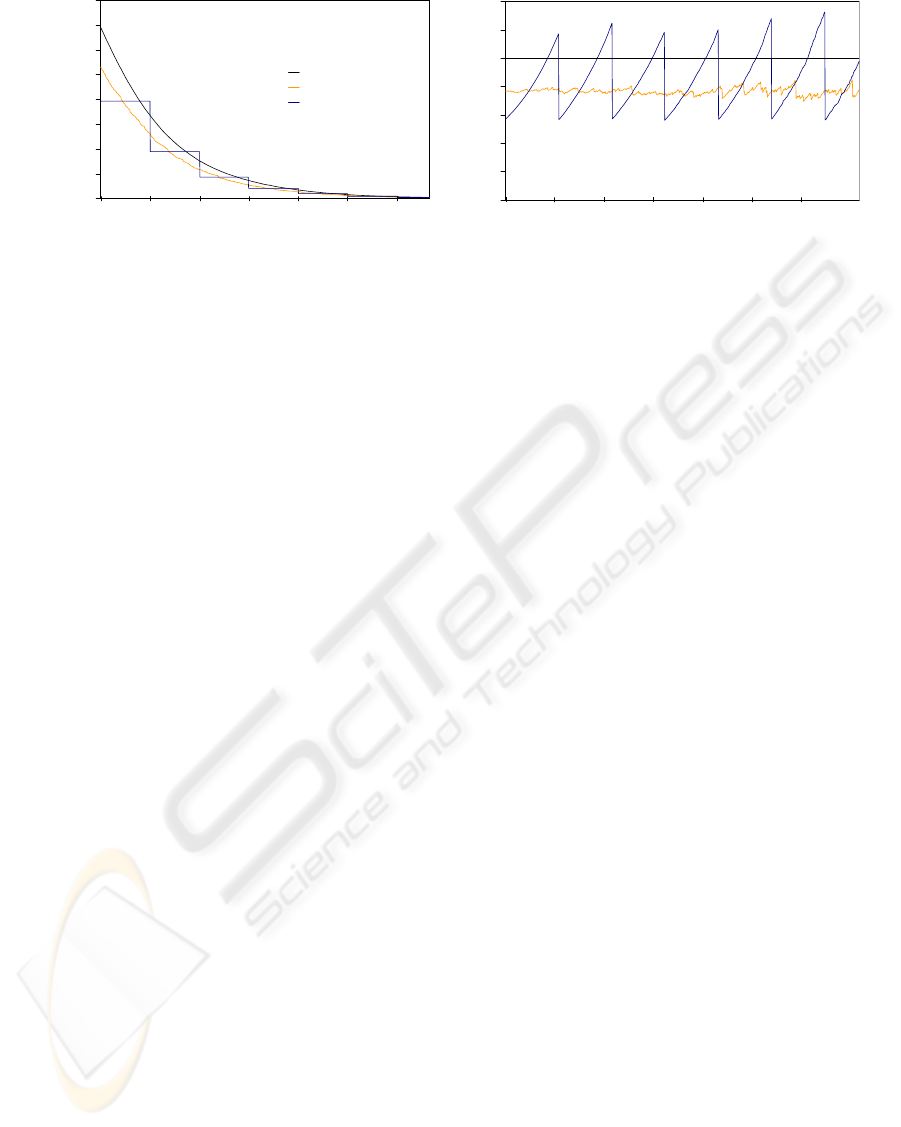
the next lower LOD. In figure 10(a) the number of
vertices used for rendering is shown for these discrete
LOD in comparison to the original hierarchy and a
hierarchy with patch size 10. As you can see, the dis-
crete LOD is better at the beginning of each distance
interval. But the reduced hierarchy adapts the number
of vertices better to distance, so that it is more effi-
cient towards the end of each interval. In figure 10(b)
the number of vertices in relation to the original hier-
archy is shown. Especially here you can see the range
of distance where our approach delivers better results
(compared to discrete LOD) exceeds the number of
distance intervals where the results are poorer, while
it also provides smooth LOD transitions, that discrete
LOD does not.
6 CONCLUSION AND FUTURE
WORK
In this paper we described a technique that allows to
use the benefits of continuous LOD (smooth LOD
transition) and discrete LOD (good striptification,
fast LOD selection). Using a fine-granular LOD-
hierarchy as a base, we reduce this by iteratively using
an introduced arc − collapse operator. This reduced
hierarchy allows the access to larger surface areas
(patches) of a specific resolution than before. Thus,
using triangle strips for these patches, a certain LOD
is described by less vertices, which yields a significant
reduction in vertices that have to be processed by the
graphics card. Since the number of vertices adapts
well to the viewing situation, our approach mostly
uses even less vertices than a discrete LOD. This is
shown by results.
Our technique works well for all kind of objects
that can be described by previous multi-resolution
techniques, too. For objects of a high complexity, like
plants, this is not the case because these objects can
not be simplified by local triangle based simplifica-
tion operations very efficiently. Thus, even the lowest
LOD contains many triangles. For such objects, point
based approaches or combined approaches using hy-
brid hierarchies in the sense of (Cohen et al., 2001)
should be preferred, because points are not defined by
edges as triangles are, but by isolated vertices. One
could imagine to use our approach for point hierar-
chies as well. Since point hierarchies mostly store
points in nodes and not in arcs, a node-collapse op-
erator is imaginable to reduce such point hierarchies.
Thus, larger amounts of points could be rendered at
once. This may accelerate point based LOD render-
ing using such reduced point hierarchies.
EFFICIENT RENDERING OF HIGH-DETAILED OBJECTS USING A REDUCED MULTI-RESOLUTION
HIERARCHY
9
0
00005
000001
000051
000002
000052
000003
000053
000004
4623618421
)elacs cimhtiragol( ecnatsid
vertices
yhcrareih lanigiro
01 ezis hctap
DoL citats
0
2.0
4.0
6.0
8.0
1
2.1
4.1
4623618421
)elacs cimhtiragol( ecnatsid
relative to original
(a) (b)
Figure 10: Processed vertices using the original hierarchy and a hierarchy of patch size 10 in comparison to discrete LOD (a)
and in relation to the original hierarchy resp. (b).
REFERENCES
Akeley, K., Haeberli, P., and Burns, D. (1990). The
tomesh.c program. In Technical report. Silicon
Graphics. 1990. Available on SGI Developers Tool-
box CD.
Cohen, J. D., Aliaga, D. G., and Zhang, W. (2001). Hy-
brid simplification: combining multi-resolution poly-
gon and point rendering. In Proceedings of the confer-
ence on Visualization ’01, pages 37–44. IEEE Com-
puter Society Press.
Duchaineau, M., Wolinsky, M., Sigeti, D. E., Aldrich, M. C.
M. C., and Mineev-Weinstein, M. B. (1997). Roam-
ing terrain: Real-time optimally adapting meshes. In
IEEE Visualization ’97, pages 81–88. IEEE Computer
Society Press.
El-Sana, J., Azanli, E., and Varshney, A. (1999). Skip strips:
maintaining triangle strips for view-dependent render-
ing. In VIS ’99: Proceedings of the conference on
Visualization ’99, pages 131–138, Los Alamitos, CA,
USA. IEEE Computer Society Press.
Evans, F., Skiena, S., and Varshney, A. (1996). Optimizing
triangle strips for fast rendering. In VIS ’96: Proceed-
ings of the 7th conference on Visualization ’96, pages
319–326, Los Alamitos, CA, USA. IEEE Computer
Society Press.
Floriani, L. D., Magillo, P., and Puppo, E. (1997). Building
and traversing a surface at variable resolution. In Pro-
ceedings of the 8th conference on Visualization ’97,
pages 103–ff. IEEE Computer Society Press.
Floriani, L. D., Magillo, P., and Puppo, E. (1998). Effi-
cient implementation of multi-triangulations. In Pro-
ceedings of the conference on Visualization ’98, pages
43–50. IEEE Computer Society Press.
Funkhouser, T. A. and Sequin, C. H. (1993). Adaptive dis-
play algorithm for interactive frame rates during vi-
sualization of complex virtual environments. In Pro-
ceedings of the 20th annual conference on Computer
graphics and interactive techniques, pages 247–254.
ACM Press.
Garland, M. and Heckbert, P. S. (1997). Surface simpli-
fication using quadric error metrics. In Proceedings
of the 24th annual conference on Computer graph-
ics and interactive techniques, pages 209–216. ACM
Press/Addison-Wesley Publishing Co.
Hoppe, H., DeRose, T., Duchamp, T., McDonald, J., and
Stuetzle, W. (1993). Mesh optimization. In SIG-
GRAPH ’93: Proceedings of the 20th annual con-
ference on Computer graphics and interactive tech-
niques, pages 19–26, New York, NY, USA. ACM
Press.
Lindstrom, P., Koller, D., Ribarsky, W., Hodges, L. F.,
Faust, N., and Turner, G. A. (1996). Real-time, con-
tinuous level of detail rendering of height fields. In
SIGGRAPH ’96: Proceedings of the 23rd annual con-
ference on Computer graphics and interactive tech-
niques, pages 109–118, New York, NY, USA. ACM
Press.
Luebke, D., Reddy, M., Cohen, J., Varshney, A., Watson,
B., and Huebner, R. (2002). Level of Detail for 3D
Graphics. Computer Graphics and Geometric Model-
ing. Morgan Kaufmann.
Stewart, A. J. (2001). Tunneling for triangle strips in con-
tinuous level-of-detail meshes. In GRIN’01: No de-
scription on Graphics interface 2001, pages 91–100,
Toronto, Ont., Canada, Canada. Canadian Information
Processing Society.
Velho, L., de Figueiredo, L. H., and Gomes, J. (1999). Hi-
erarchical generalized triangle strips. In The Visual
Computer, volume 15, pages 21–35. Springer-Verlag
GmbH.
Xia, J. C., El-Sana, J., and Varshney, A. (1997). Adaptive
real-time level-of-detail-based rendering for polygo-
nal models. IEEE Transactions on Visualization and
Computer Graphics, 3(2):171–183.
GRAPP 2006 - COMPUTER GRAPHICS THEORY AND APPLICATIONS
10
