
SOFTWARE IMPLEMENTATION OF THE IEEE 754R DECIMAL
FLOATING-POINT ARITHMETIC
Marius Cornea, Cristina Anderson, Charles Tsen
Intel Corporation
Keywords: IEEE 754R, IEEE 754, Floating-Point, Binary Floating-Point, Decimal Floating-Point, Basic Operations,
Algorithms, Fin
ancial Computation, Financial Calculation.
Abstract: The IEEE Standard 754-1985 for Binary Floating-Point Arithmetic (IEEE Std. 754, 1985) is being revised
(IEEE Std. 754R Draft, 2006), and an important addition to the current text is the definition of decimal
floating-point arithmetic (Cowlishaw, 2003). This is aimed mainly to provide a robust, reliable framework
for financial applications that are often subject to legal requirements concerning rounding and precision of
the results in the areas of banking, telephone billing, tax calculation, currency conversion, insurance, or
accounting in general. Using binary floating-point calculations to approximate decimal calculations has led
in the past to the existence of numerous proprietary software packages, each with its own characteristics and
capabilities. New algorithms are presented in this paper which were used for a generic implementation in
software of the IEEE 754R decimal floating-point arithmetic, but may also be suitable for a hardware
implementation. In the absence of hardware to perform IEEE 754R decimal floating-point operations, this
new software package that will be fully compliant with the standard proposal should be an attractive option
for various financial computations. The library presented in this paper uses the binary encoding method
from (IEEE Std. 754R Draft, 2006) for decimal floating-point values. Preliminary performance results
show one to two orders of magnitude improvement over a software package currently incorporated in GCC,
which operates on values encoded using the decimal method from (IEEE Std. 754R Draft, 2006).
1 INTRODUCTION
Binary floating-point arithmetic can be used in most
cases to approximate decimal calculations. However
errors may occur when converting numerical values
between their binary and decimal representations,
and errors can accumulate differently in the course
of a computation depending on whether it is carried
out using binary or decimal floating-point
arithmetic.
For example, the following simple C program will
not
have in general the expected output b=7.0 for
a=0.0007.
main () {
float a, b;
a = 7/10000.0;
b = 10000.0 * a;
printf ("a = %x = %10.10f\n",
*(unsigned int *)&a, a);
printf ("b = %x = %10.10f\n",
*(unsigned int *)&b, b);
}
(The value 7.0 has the binary encoding
0
x40e00000.) The actual output on a system that
complies with the IEEE Standard 754 will be:
a = 3a378034 = 0.0007000000
b = 40dfffff = 6.9999997504
Such errors are not acceptable in many cases of
fina
ncial computations, mainly because legal
requirements mandate how to determine the
rounding errors - in general following rules that
humans would use when performing the same
computations on paper, and in decimal. Several
software packages exist and have been used for this
purpose so far, but each one has its own
characteristics and capabilities such as precision,
rounding modes, operations, or internal storage
formats for numerical data. These software packages
are not compatible with each other in general. The
IEEE 754R standard proposal attempts to resolve
these issues by defining all the rules for decimal
floating-point arithmetic in a way that can be
adopted and implemented on all computing systems
in software, in hardware, or in a combination of the
13
Cornea M., Anderson C. and Tsen C. (2006).
SOFTWARE IMPLEMENTATION OF THE IEEE 754R DECIMAL FLOATING-POINT ARITHMETIC.
In Proceedings of the First International Conference on Software and Data Technologies, pages 13-20
DOI: 10.5220/0001320900130020
Copyright
c
SciTePress

two. Using IEEE 754R decimal floating-point
arithmetic, the previous example could then become:
main () {
decimal32 a, b;
a = 7/10000.0;
b = 10000.0 * a;
printf ("a = %x = %10.10fd\n",
*(unsigned int *)&a, a);
printf ("b = %x = %10.10fd\n",
*(unsigned int *)&b, b);
}
(The hypothetical format descriptor %fd is used for
printing decimal floating-point values.) The output
on a system complying with the IEEE Standard
754R proposal would then represent the result
without any error:
a = 30800007 = 0.0007000000
b = 32800007 = 7.0000000000
(The IEEE 754R binary encoding for decimal
floating-point values was used in this example.) The
following section summarizes the most important
aspects of the IEEE 754R decimal floating-point
arithmetic definition.
2 IEEE 754R DECIMAL
FLOATING-POINT
The IEEE 754R standard proposal defines three
decimal floating-point formats with sizes of 32, 64,
and 128 bits. Two encodings for each of these
formats are specified: a decimal-based encoding
which is best suited for certain possible hardware
implementations of the decimal arithmetic (Erle et
al, 2005), and a binary-based encoding better suited
for software implementations on systems that
support the IEEE 754 binary floating-point
arithmetic in hardware (Tang, 2005). The two
encoding methods are otherwise equivalent, and a
simple conversion operation is necessary to switch
between the two.
As defined in the IEEE 754R proposal, a decimal
floating-point number n is represented as
n = ±C 10
e
where C is a positive integer coefficient with at most
p decimal digits, and e is an integer exponent. A
precision of p decimal digits will be assumed further
for the operands and results of decimal floating-
point operations.
Compared to the binary single, double, and quad
precision floating-point formats, the decimal
floating-point formats denoted here by decimal32,
decimal64, and decimal128 cover different ranges
and have different precisions, although they have
similar storage sizes. For decimal, only the wider
formats are used in actual computations, while
decimal32 is defined as a storage format only. For
numerical values that can be represented in these
binary and decimal formats, the main parameters
that determine their range and precision are shown
in Table 1.
Table 1: IEEE 754 binary and IEEE 754R decimal
floating-point format parameters.
Binary Formats
single double quad
Prec. n=24 n=53 n=113
E
min
–126 –1022 –16382
E
max
+127 +1023 +16383
Decimal Formats
decimal32 decimal64 decimal128
Prec. p=7 p=16 p=34
E
min
–101 –398 –6178
E
max
+90 +369 +6111
The following sections will present new algorithms
that can be used for an efficient implementation in
software of the decimal floating-point arithmetic as
defined by the IEEE 754R proposal. Mathematical
proofs of correctness have been developed, but will
not be included here for brevity. Compiler and run-
time support libraries could use the implementation
described here, which addresses the need to have a
good software solution for the decimal floating-point
arithmetic.
3 CONVERSIONS BETWEEN
DECIMAL AND BINARY
FORMATS
In implementing the decimal floating-point
arithmetic defined in IEEE 754R, conversions
between decimal and binary formats are necessary in
many situations.
For example, if decimal floating-point values are
encoded in a decimal-based format (string, BCD,
IEEE 754R decimal encoding, or other) they need to
be converted to binary before a software
implementation of the decimal floating-point
operation can take full advantage of the existing
hardware for binary operations. This conversion is
relatively easy to implement, and should exploit any
available instruction-level parallelism.
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
14

The opposite conversion, from binary to decimal
format may have to be performed on results before
writing them to memory, or for printing in string
format decimal numbers encoded in binary.
Another reason for binary-to-decimal conversion
could be for rounding a decimal floating-point result
to a pre-determined number of decimal digits, if the
exact result was calculated first in binary format.
The straightforward method for this is to convert the
exact result to decimal, round to the destination
precision and then, if necessary, convert the
coefficient of the final result back to binary. This
step can be avoided completely if the coefficients
are stored in binary.
The mathematical property presented next was used
for this purpose. It gives a precise way to ‘cut off’ x
decimal digits from the lower part of an integer C
when its binary representation is available, thus
avoiding the need to convert C to decimal, remove
the lower x decimal digits, and then convert the
result back to binary. This property was applied to
conversions from binary to decimal format as well
as in the implementation of the most common
decimal floating-point operations: addition,
subtraction, multiplication, fused multiply-add, and
in part, division.
For example if the decimal number C = 123456789
is available in binary and its six most significant
decimal digits are required, Property 1 specifies
precisely how to calculate the constant k
3
≈ 10
-3
so
that ⎣C k
3
⎦ = 123456, with certainty, while
using only the binary representation of C. The
values k
x
are pre-calculated. (Note: the floor(x),
ceiling(x), and fraction(x) functions are denoted here
by ⎣x⎦, ⎡x⎤ , and {x} respectively.)
Property 1.
Let C N be a number in base b = 2 and
C = d
0
10
q-1
+ d
1
10
q-2
+ … + d
q-2
10
1
+ d
q-1
its
representation in base B=10, where d
0
, d
1
, … d
q-1
{0, 1, … , 9} and d
0
≠ 0.
Let x {1, 2, 3, …, q–1} and G = log
2
10.
If y N, y ⎡{G x} + G q⎤ and k
x
is the
value of 10
-x
rounded up to y bits (the subscript RP,y
indicates rounding up y bits in the significand), i.e.:
k
x
= (10
-x
)
RP,y
= 10
–x
(1 + ε) 0 < ε < 2
–y+1
then ⎣C k
x
⎦ = d
0
10
q-x-1
+ d
1
10
q-x-2
+ d
2
10
q-
x-3
+ … + d
q-x-2
10
1
+ d
q-x-1
Given an integer C represented in binary, this
property specifies a method to remove exactly x
digits from the lower part of the decimal
representation of C, without actually converting the
number to a decimal representation. The property
specifies the minimum number of bits y that are
necessary in an approximation of 10
-x
, so that the
integer part (or ‘floor’) of C k
x
will be precisely
the desired result. The property states that y ⎡{G
x} + G q⎤ . However, in practice it is sufficient
to take y = ⎡1 + G q⎤ = 1 + ⎡G q⎤ where ⎡G
q⎤ is the ‘ceiling’ of G q (e.g. ⎡33.3⎤ = 34). Note
that ρ = log
2
10 ≈ 3.3219… and 2
ρ
= 10. For example
if we want to remove the x lower decimal digits of a
16-digit decimal number, we can multiply the
number with an approximation of 10
-x
rounded up to
y = 1 + ⎡G 16⎤ = 55 bits, followed by removal of
the fractional part in the product.
The relative error ε associated with the
approximation of 10
–x
which was rounded up to y
bits satisfies 0 < ε < 2
–y+1
= 2
–⎡ρ·q⎤
.
The values k
x
for all x of interest are pre-calculated
and are stored as pairs (K
x
, e
x
), with K
x
and e
x
positive integers:
k
x
= K
x
· 2
–ex
This allows for implementations exclusively in the
integer domain of some decimal floating-point
operations, in particular addition, subtraction,
multiplication, fused multiply-add, and certain
conversions.
4 DECIMAL FLOATING-POINT
ADDITION
It will be assumed that
n1 = C1 · 10
e1
C1 ∈ Z, 0 < C1 < 10
p
n2 = C2 · 10
e2
C2 ∈ Z, 0 < C2 < 10
p
are two non-zero decimal floating-point numbers
with coefficients having at most p decimal digits
stored as binary integers and that their sum has to be
calculated, rounded to p decimal digits using the
current IEEE rounding mode (this is indicated by the
subscript rnd,p).
n = (n1 + n2)
rnd,p
= C · 10
e
The coefficient C needs to be correctly rounded, and
is stored as a binary integer as well. For simplicity, it
will be assumed that n1 ≥ 0 and e1 ≥ e2. (The rules
for other combinations of signs or exponent ordering
can be derived from here.)
If the exponent e1 of n1 and the exponent e2 of n2
differ by a large quantity, the operation is simplified
and rounding is trivial because n2 represents just a
rounding error compared to n1. Otherwise if e1 and
e2 are relatively close the coefficients C1 and C2
will ‘overlap’, the coefficient of the exact sum may
have more than p decimal digits, and so rounding
may be necessary. All the possible cases will be
quantified next.
If the exact sum is n’, let C’ be the exact (not yet
rounded) sum of the coefficients:
n’ = n1 + n2 = C1 · 10
e1
+ C2 · 10
e2
=
(C1 · 10
e1 – e2
+ C2) · 10
e2
C’ = C1 · 10
e1 – e2
+ C2
SOFTWARE IMPLEMENTATION OF THE IEEE 754R DECIMAL FLOATING-POINT ARITHMETIC
15

Let q1, q2, and q be the numbers of decimal digits
needed to represent C1, C2, and C’. If not zero, the
rounded coefficient C will require between 1 and p
decimal digits. Rounding is not necessary if C’
represented in decimal requires at most p digits, but
it is necessary otherwise.
If q ≤ p, then the result is exact:
n = (n’)
rnd,p
= (C’ · 10
e2
)
rnd,p
=
(C’)
rnd,p
· 10
e2
= C’ · 10
e2
Otherwise, if q > p let x = q – p ≥ 1. Then:
n = (n’)
rnd,p
= (C’ · 10
e2
)
rnd,p
=
(C’)
rnd,p
· 10
e2
= C · 10
e2+x
If after rounding C = 10
p
(rounding overflow), then
n =10
p-1
· 10
e2+x+1
.
A simple analysis shows that rounding is trivial if q1
+ e1 – q2 – e2 ≥ p. If this is not the case, i.e. if
|q1 + e1 – q2 – e2| ≤ p – 1
then the sum C’ has to be calculated and it has to be
rounded to p decimal digits. This case can be
optimized by separating it in sub-cases as shall be
seen further.
The algorithm presented next uses Property 1 in
order to round correctly (to the destination precision)
the result of a decimal floating-point addition in
rounding to nearest mode, and also determines
correctly the exactness of the result by using a
simple comparison operation. First, an
approximation of the result’s coefficient is
calculated using Property 1. This will be either the
correctly rounded coefficient, or it will be off by one
ulp (unit-in-the-last-place). The correct result as well
as its exactness can be determined directly from the
calculation, without having to compute a remainder
through a binary multiplication followed by a
subtraction for this purpose. This makes the
rounding operation for decimal floating-point
addition particularly efficient.
Decimal Floating-Point Addition with Rounding
to Nearest
The straightforward method to calculate the result is
to convert both coefficients to a decimal encoding,
perform a decimal addition, round the exact decimal
result to nearest to the destination precision, and
then convert the coefficient of the final result back to
binary. It would also be possible to store the
coefficients in decimal all the time, but then neither
software nor hardware implementations could take
advantage easily of existing instructions or circuitry
that operate on binary numbers. The algorithm used
for decimal floating-point addition in rounding to
nearest mode is Algorithm 1, shown further.
If the smaller operand represents more than a
rounding error in the larger operand, the sum C’ =
C1 · 10
e1–e2
+ C2 is calculated. If the number of
decimal digits q needed to represent this number
does not exceed the precision p of the destination
format, then no rounding is necessary and the result
is exact. If q > p, then x = q – p decimal digits have
to be removed from the lower part of C’, and C’ has
to rounded correctly to p decimal digits. For correct
rounding to nearest, 0.5 ulp is added to C’: C’’ = C’
+ 1/2 · 10
x
. The result is multiplied by k
x
≈ 10
-x
(C*
= C’’ · k
x),
where the pre-calculated values k
x
are
stored for all x {1, 2, …, p}. A test for midpoints
follows (0 < f* < 10
–p
, where f* is the fractional part
of C*) and if affirmative, the result is rounded to the
nearest even integer. (For example if the exact result
4567.5 has to be rounded to nearest to four decimal
places, the rounded result will be 4568.) Next the
algorithm checks for rounding overflow (p+1
decimal digits are obtained instead of p) and finally
it checks for exactness.
Note that the straightforward method for the
determination of midpoints and exactness is to
calculate a remainder r = C’ – C 10
x
∈[0, 10
x
).
Midpoint results could be identified by comparing
the remainder with 1/2·10
x
, and exact results by
comparing the remainder with 0. However, the
calculation of a remainder – a relatively costly
operation – was avoided in Algorithm 1 and instead
a single comparison to a pre-calculated constant was
used. This simplified method to determine midpoints
and exactness along with the ability to use Property
1 make Algorithm 1 more efficient for decimal
floating-point addition than previously known
methods.
Algorithm 1. Calculate the sum of two decimal
floating-point numbers rounded to nearest to p
decimal digits, and determine its exactness.
q1, q2 = number of decimal digits needed to
represent C1, C2 // from table lookup
if |q1 + e1 – q2 – e2| ≥ p then
// assuming that e1 ≥ e2 round the result
// directly as 0 < C2 < 1 ulp (C1 · 10
e1–e2
);
the result n = C1 · 10
e1
or
n = C1 · 10
e1
± 10
e1+q1–p
is inexact
else // if |q1 + e1 – q2 – e2| ≤ p – 1
C’ = C1 · 10
e1–e2
+ C2 // binary integer
// multiplication and addition;
// 10
e1–e2
from table lookup
q = number of decimal digits needed to
represent C’ // from table lookup
if q ≤ p the result n = C’ 10
e2
is exact
else if q ∈ [p+1, 2·p] continue
x = q – p, number of decimal digits to be
removed from lower part of C’, x ∈ [1, p]
C’’ = C’ + 1/2 · 10
x
// 1/2 · 10
x
// pre-calculated, from table lookup
k
x
= 10
–x
(1 + ε), 0 < ε < 2
–⎡2·ρ·p⎤
/ / pre-calculated as specified in Property 1
C* = C’’ · k
x
= C’’ · K
x
· 2
–Ex
// binary integer multiplication with
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
16

// implied binary point
f* = the fractional part of C*
// consists of the lower Ex bits of the
// product C’’ · K
x
if 0 < f* < 10
–p
then
if ⎣C*⎦ is even then C = ⎣C*⎦
// logical shift right;
// C has p decimal digits,
// correct by Property 1
else if ⎣C*⎦ is odd then C = ⎣C*⎦ – 1
// logical shift right; C has p dec.
// digits, correct by Property 1
else C = ⎣C*⎦ // logical shift right; C has p
// decimal digits, correct by Property 1
n = C 10
e2+x
if C = 10
p
then n = 10
p–1
10
e2+x+1
// rounding overflow
if 0 < f* – 1/2 < 10
–p
then the result is exact
else it is inexact
Note that conditions 0 < f* < 10
–p
and 0 < f* – 1/2 <
10
–p
from Algorithm 1 for midpoint detection and
exactness determination hold also if 10
–p
is replaced
by 10
–x
or even by k
x
= 10
–x
(1 + ε). These
comparisons are fairly easy in practice. For example,
since C’’·k
x
= C’’·K
x
·2
–ex
, in f*<10
–p
the bits shifted
to the right out of C’’·k
x
, representing f* can be
compared with a pre-calculated constant that
approximates 10
–p
(or 10
–x
).
Decimal Floating-Point Addition when Rounding
to Zero, Down, or Up
The method to calculate the result when rounding to
zero or down is similar to that for rounding to
nearest. The main difference is that the step for
calculating C’’ = C’ + 1/2 · 10
x
is not necessary
anymore, because midpoints between consecutive
floating-point numbers do not have a special role
here. For rounding up, the calculation of the result
and the determination of its exactness are identical
to those for rounding down. However, when the
result is inexact then one ulp has to be added to it.
5 DECIMAL FLOATING-POINT
MULTIPLICATION
It will be assumed that the product
n = (n1 · n2)
rnd,p
= C · 10
e
has to be calculated, where the coefficient C of n is
correctly rounded to p decimal digits using the
current IEEE rounding mode, and is stored as a
binary integer. The operands n1 = C1 · 10
e1
and n2
= C2 · 10
e2
are assumed to be strictly positive (for
negative numbers the rules can be derived directly
from here). Their coefficients require at most p
decimal digits to represent and are stored as binary
integers, possibly converted from a different
format/encoding.
Let q be the number of decimal digits required to
represent the full integer product C’ = C1 · C2 of the
coefficients of n1 and n2. Actual rounding to p
decimal digits will be necessary only if q ∈ [p+1,
2·p], and will be carried out using Property 1. In all
rounding modes the constants k
x
≈ 10
–x
used for this
purpose, where x = q – p, are pre-calculated to y bits
as specified in Property 1. Since q ∈ [p+1, 2·p] for
situations where rounding is necessary, all cases are
covered correctly by choosing y = 1+ ⎡2·ρ·p⎤.
Similar to the case of the addition operation, the pre-
calculated values k
x
are stored for all x {1, 2, …,
p}.
Decimal Floating-Point Multiplication with
Rounding to Nearest
The straightforward method to calculate the result is
similar to that for addition. A new and better method
for decimal floating-point multiplication with
rounding to nearest that uses existing hardware for
binary computations is presented in Algorithm 2. It
uses Property 1 to avoid the need to calculate a
remainder for the determination of midpoints or
exact floating-point results, as shall be seen further.
The multiplication algorithm has many similarities
with the algorithm for addition.
Algorithm 2. Calculate the product of two
decimal floating-point numbers rounded to
nearest to p decimal digits, and determine its
exactness.
C’ = C1 · C2 // binary integer multiplication
q = the number of decimal digits required to
represent C’ // from table lookup
if q ≤ p then the result n = C’ 10
e1+e2
is exact else
if q ∈ [p+1, 2·p] continue
x = q – p, the number of decimal digits to be
removed from the lower part of C’, x ∈ [1, p]
C’’ = C’ + 1/2 · 10
x
// 1/2 · 10
x
pre-calculated
k
x
= 10
–x
(1 + ε), 0 < ε < 2
–⎡2·ρ·p⎤
// pre-calculated
// as specified in Property 1
C* = C’’ · k
x
= C’’ · K
x
· 2
–Ex
// binary integer
// multiplication with implied binary point
f* = the fractional part of C* // consists of the
// lower E
x
bits of the product C’’ · K
x
if 0 < f* < 10
–p
then // since C* = C’’· K
x
· 2
–Ex
,
// compare E
x
bits shifted out of C* with 0
// and with 10
–p
if ⎣C*⎦ is even then C = ⎣C*⎦ // logical right
// shift; C has p decimal digits, correct by
// Property 1
else C = ⎣C*⎦ – 1 // if ⎣C*⎦ is odd // logical
// right shift; C has p decimal digits, correct
// by Property 1
SOFTWARE IMPLEMENTATION OF THE IEEE 754R DECIMAL FLOATING-POINT ARITHMETIC
17

else
C = ⎣C*⎦ // logical shift right; C has p
// decimal digits, correct by Property 1
n = C 10
e1+e2+x
// rounding overflow
if 0 < f* – 1/2 < 10
–p
then the result is exact
else the result is inexact
// C* = C’’ · K
x
· 2
–Ex
⇒ compare E
x
bits
// shifted out of C* with 1/2 and 1/2+10
–p
If q ≥ p + 1 the result is inexact unless the x decimal
digits removed from the lower part of C’’ · k
x
were
all zeros. To determine whether this was the case,
just as for addition, the straightforward method is to
calculate a remainder r = C’ – C 10
x
∈[0, 10
x
).
Midpoint results could be identified by comparing
the remainder with 1/2·10
x
, and exact results by
comparing the remainder with 0. However, the
calculation of a remainder – a relatively costly
operation – was avoided in Algorithm 2 and instead
a single comparison to a pre-calculated constant was
used.
The simplified method to determine midpoints and
exactness along with the ability to use Property 1
make Algorithm 2 better for decimal floating-point
multiplication than previously known methods.
Decimal Floating-Point Multiplication when
Rounding to Zero, Down, or Up
The method to calculate the result when rounding to
zero or down is similar to that for rounding to
nearest. Just as for addition, the step for calculating
C’’ = C’ + 1/2 · 10
x
is not necessary anymore.
Exactness is determined using the same method as in
Algorithm 2. For rounding up, the calculation of the
result and the determination of its exactness are
identical to those for rounding down. However,
when the result is inexact then one ulp has to be
added to it.
6 DECIMAL FLOATING-POINT
DIVISION
It will be assumed that the quotient
n = (n1 / n2)
rnd,p
= C · 10
e
has to be calculated where n1 > 0, n2 > 0, and q1,
q2, and q are the numbers of decimal digits needed
to represent C1, C2, and C (the subscript rnd,p
indicates rounding to p decimal digits, using the
current rounding mode). Property 1 cannot be
applied efficiently for the calculation of the result in
this case because a very accurate approximation of
the exact quotient is expensive to calculate. Instead,
a combination of integer operations and floating-
point division allow for the determination of the
correctly rounded result. Property 1 is used only
when an underflow is detected and the calculated
quotient has to be shifted right a given number of
decimal positions. The decimal floating-point
division algorithm is based on Property 2 presented
next.
Property 2. If a, b are two positive integers and m
∈ N, m ≥ 1 such that b < 10
m
, a/b < 10
m
and n ≥
⎣m⋅log
2
10⎦ , then | a/b– ⎣((a)
rnd,n
/(b)
rnd,n
)
rnd,n
⎦ | < 8.
The decimal floating-point division algorithm for
operands n1 = C1⋅10
e1
and n2 = C2⋅10
e2
follows.
While this algorithm may be rather difficult to
follow without working out an example in parallel, it
is included here for completeness. Its correctness, as
well as that of all the other algorithms presented here
has been verified.
Algorithm 3. Calculate the quotient of two
decimal floating-point numbers, rounded to p
decimal digits in any rounding mode, and
determine its exactness.
if C1 < C2
find the integer d > 0 such that (C1/C2)⋅10
d
∈
[1, 10).
// compute d based on the number
// of decimal digits q1, q2 in C1, C2
C1’ = C1⋅10
d+15
, Q = 0
e = e1 – e2 – d – 15 // expected res. expon.
else
a = (C1 OR 1)
rnd,n
, b = (C2)
rnd,n
// logical OR
Q = ⎣((a/b)
rnd,n
)⎦
R = C1 – Q ⋅ C2
if R < 0
Q = Q – 1
R = R + C2
if R = 0 the result n = Q ⋅ 10
e1–e2
is exact
else continue
find the number of decimal digits for Q: d >
0 such that Q ∈ [10
d–1
, 10
d
)
C1’ = R ⋅ 10
16–d
Q = Q ⋅ 10
16–d
e = e1 – e2 – 16 + d
Q2 = ⎣((C1’)
rnd,n
/(C2)
rnd,n
)
rnd,n
⎦
R = C1’ – Q2 ⋅ C2
Q = Q + Q2
if R ≥ 4 ⋅ C2
Q = Q + 4
R = R – 4 ⋅ C2
if R ≥ 2 ⋅ C2
Q = Q + 2
R = R – 2 ⋅ C2
if R ≥ C2
Q = Q + 1
R = R – C2
if e ≥ minimum_decimal_exponent
apply rounding in desired mode by
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
18

comparing R and C2
// e.g. for rounding to nearest add 1 to Q
// if 5 ⋅ C2 < 10 ⋅ R + (Q AND 1)
the result n = Q ⋅10
e
is inexact
else
result underflows
compute the correct result based on Prop. 1
7 DECIMAL FLOATING-POINT
SQUARE ROOT
Assume that the square root
n = (√n1)
rnd,p
= C · 10
e
has to be calculated (where the subscript rnd,p
indicates rounding to p decimal digits using the
current rounding mode). The method used for this
computation is based on Property 3 and Property 4,
shown next. A combination of integer and floating-
point operations are used. It will be shown next that
the minimum precision n of the binary floating-point
numbers that have to be used in the computation of
the decimal square root for decimal64 arguments
(with p = 16) is n = 53, so the double precision
floating-point format can be used. The minimum
precision n of the binary floating-point numbers that
have to be used in the computation of the square root
for decimal128 arguments (with p = 34) is n = 113,
so the quad precision floating-point format can be
used safely.
Properties 3 and 4 as well as the algorithm for
square root calculation are included here for
completeness.
Property 3. If x ∈ (1, 4) is a binary floating-point
number with precision n and s = (
x
)
RN,n
is its square root rounded to nearest to n bits, then s
+ 2
–n
< x.
Property 4. Let m be a positive integer and n =
⎣m⋅log
2
10+0.5⎦. For any integer C∈[10
2⋅m–2
, 10
2⋅m
),
the inequality |
C –⎣√((C)
RN,n
)⎦ < 3/2 is true.
The round-to-nearest decimal square root algorithm
can now be summarized as follows:
Algorithm 4. Calculate the square root of a
decimal floating-point number n1 = C⋅10
e
,
rounded to nearest to p decimal digits, and
determine its exactness.
if e is odd then
e’ = e – 1
C’ = C ⋅ 10
else
e’ = e
C’ = C
let S = ⎣√(( C’)
RN,n
)⎦
if S * S = C’
the result n = S ⋅ 10
e’/2
is exact
else
q = number of decimal digits in C
C’’ = C’ ⋅ 10
2⋅p–1–q
and Q = ⎣√(( C’’)
RN,n
)⎦
if (C’’ – Q ⋅ Q < 0) sign = –1 else sign = 1
M = 2⋅Q + sign // will check against this
// midpoint for rounding to nearest
if (M ⋅ M – 4 ⋅ C’’ < 0) sign_m = –1
else sign_m = 1
if sign ≠ sign_m Q’ = Q + sign else Q’ = Q
the result n = Q’ ⋅ 10
e’/2
is inexact
Decimal Floating-Point Square Root when
Rounding to Zero, Down, or Up
The algorithm shown above can be easily adapted
for other rounding modes. Once Q is computed such
that |
'C'
– Q| < 1.5, one needs to consider
rounding the result coefficient to one of the
following values: Q–2, Q–1, Q, Q+1, Q+2, and only
two of these values need to be considered after the
sign of (
'C'
– Q) has been computed.
8 CONCLUSIONS
A new generic implementation in C of the basic
operations for decimal floating-point arithmetic
specified in the IEEE 754R standard proposal was
completed, based on new algorithms presented in
this paper. Several other operations were
implemented that were not discussed here for
example remainder, fused multiply-add, comparison,
and various conversion operations. Performance
results for all basic operations were in the expected
range, for example the latency of decimal128
operations is comparable to that of binary quad
precision operations implemented in software.
It was also possible to compare the performance of
the new software package for basic operations with
that of the decNumber package contributed to GCC
(Grimm, 2005). The decNumber package represents
the only other implementation of the IEEE 754R
decimal floating-point arithmetic in existence at the
present time. It should be noted that decNumber is a
more general decimal arithmetic library in ANSI C,
suitable for commercial and human-oriented
applications (decNumber, 2005). It allows for
integer, fixed-point, and decimal floating-point
computations, and supports arbitrary precision
values (up to a billion digits).
Tests comparing the new decimal floating-point
library using the algorithms described in this paper
versus decNumber showed that the new generic C
implementations for addition, multiplication,
SOFTWARE IMPLEMENTATION OF THE IEEE 754R DECIMAL FLOATING-POINT ARITHMETIC
19
division, square root, and other operations were
faster than the decNumber implementations, in most
cases by one to two orders of magnitude.
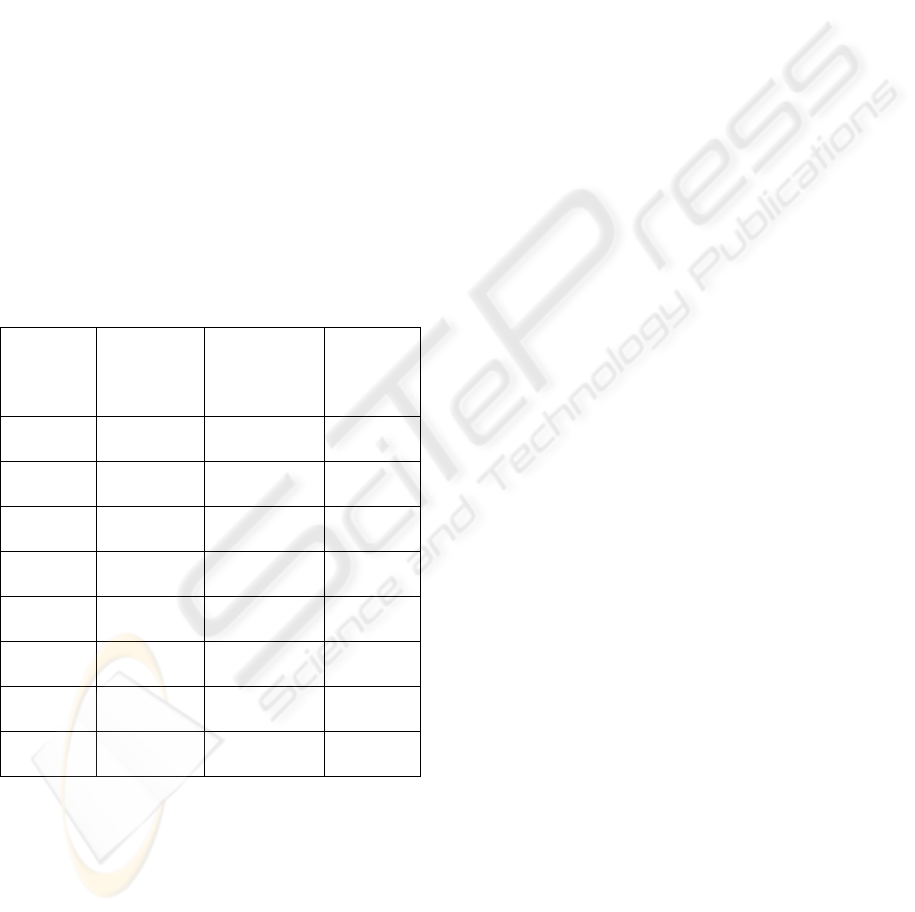
Table 2 shows the results of this comparison for
basic 64-bit and 128-bit decimal floating-point
operations measured on a 3.4 GHz Intel® EM64t
system with 4 GB of RAM, running Microsoft
Windows Server 2003 Enterprise x64 Edition SP1.
The code was compiled with the Intel(R) C++
Compiler for Intel(R) EM64T-based applications,
Version 9.0. The three values presented in each case
represent minimum, median, and maximum values
for a small data set covering operations from very
simple (e.g. with operands equal to 0 or 1) to more
complicated, e.g. on operands with 34 decimal digits
in the 128-bit cases. For the new library, further
performance improvements can be attained by fine-
tuning critical code sequences or by optimizing
simple, common cases.
Table 2: New Decimal Floating-Point Library
Performance vs. decNumber on EM64t (3.4 GHz Xeon).
Minimum-median-maximum values are listed in sequence,
after subtracting the call overhead.
Oper-
ation
New
Library
[clock
cycles]
decNumber
Library
[clock
cycles]
dec
Number
/New
Library
64-bit
ADD
14-140-
241
99-1400-
1741
4-10-14
64-bit
MUL
21-120-
215
190-930-
1824
6-8-9
64-bit
DIV
172-330-
491
673-2100-
3590
4-6-11
64-bit
SQRT
15-288-
289
82-16700-
18730
7-58-107
128-bit
ADD
16-170-
379
97-2300-
3333
4-13-14
128-bit
MUL
19-300-
758
95-3000-
4206
5-10-18
128-bit
DIV
153-250-
1049
1056-2000-
7340
4-8-9
128-bit
SQRT
16-700-
753
61-42000-
51855
4-60-152
For example for the 64-bit addition operation the
new implementation, using the 754R binary
encoding for decimal floating-point, took between
14 and 241 clock cycles per operation, with a
median value around 140 clock cycles. For the same
operand values decNumber, using the 754R decimal
encoding, took between 99 and 1741 clock cycles,
with a median around 1400 clock cycles. The ratio
shown in the last column was between 4 and 14,
with a median of around 10 (probably the most
important of the three values).
It is also likely that properties and algorithms
presented here for decimal floating-point arithmetic
can be applied as well for a hardware
implementation, with re-use of existing circuitry for
binary operations. It is the authors’ hope that the
work described here will represent a step forward
toward reliable and efficient implementations of the
IEEE 754R decimal floating-point arithmetic.
REFERENCES
IEEE Standard 754-1985 for Binary Floating-Point
Arithmetic. IEEE, 1985
Draft of the Revised IEEE Standard 754-1985,
http://754r.ucbtest.org/drafts/754r.pdf
Michael Cowlishaw, Decimal Floating-Point: Algorism
for Computers 2003, 16
th
IEEE Symposium on
Computer Arithmetic.
M. Erle, E, Schwarz, and M. Schulte, Decimal
Multiplication with Efficient Partial Product
Generation, 17
th
Symposium on Computer Arithmetic,
2005
Peter Tang, BID Format, IEEE 754R Draft
http://754r.ucbtest.org/subcommittee/bid.pdf
Jon Grimm, Decimal Floating-Point Extension for C via
decNumber, IBM, GCC Summit, 2005
(decNumber,2005)http://www.alphaworks.ibm.com/tech/d
ecnumber
ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES
20
