AN ANALYSIS OF THE EFFECTS OF SPATIAL LOCALITY ON THE

CACHE PERFORMANCE OF BINARY SEARCH TREES

Thomas B. Puzak

The University of Connecticut

Storrs, Connecticut, USA

Chun-Hsi Huang

The University of Connecticut

Storrs, Connecticut, USA

Keywords:

Cache Aware Binary Trees, Binary Tree Spatial Locality, Binary Tree Cache Performance.

Abstract:

The topological structure of binary search trees does not translate well into the linear nature of a computer’s

memory system, resulting in high cache miss rates on data accesses. This paper analyzes the cache perfor-

mance of search operations on several varieties of binary trees. Using uniform and nonuniform key distri-

butions, the number of cache misses encountered per search is measured for Vanilla, AVL, and two types of

Cache Aware Trees. Additionally, concrete measurements of the degree of spatial locality observed in the

trees is provided. This allows the trees to be evaluated for situational merit, and for deﬁnitive explanations

of their performance to be given. Results show that the balancing operations of AVL trees effectively negates

any spatial locality gained through naive allocation schemes. Furthermore, for uniform input, this paper shows

that large cache lines are only beneﬁcial to trees that consider the cache’s line size in their allocation strat-

egy. Results in the paper demonstrate that adaptive cache aware allocation schemes that approximate the

key distribution of a tree have universally better performance than static systems that favor a particular key

distribution.

1 INTRODUCTION

Binary trees are an attractive data structure for rep-

resenting large data sets because they exhibit an ex-

pected sub-linear search complexity. Unfortunately,

because they are a pointer based data structure, bi-

nary trees perform poorly with respect to caches. This

problem is exacerbated with balanced binary trees,

which guarantee lg n search complexity, because the

tree’s balancing operations destroy any inherent spa-

tial locality present when the keys were initially in-

serted.

The poor cache performance of a binary tree is in

direct contrast with static data structures like arrays.

While an array will exhibit good cache performance,

especially with large cache lines, its search complex-

ity is an undesirable O(n). Therefore the choice to

use a binary tree represents a trade-off, in which the

user improves his search complexity at the cost of de-

graded cache performance.

The focus of this paper is to study the L1 data

cache performance of various binary trees with spe-

cial consideration given to the spatial locality of the

data stored within the tree. Previous research has cited

spatial locality as a reason for the observed experi-

mental results measuring the cache performance of

pointer based data structures, but no concrete measure

of spatial locality in the data structures has been pro-

vided. This paper provides a method and formula for

quantifying the degree of spatial locality inherent in a

tree’s structure based on the number of cache misses

taken while accessing the tree.

Two classical binary trees, vanilla (naive) and AVL,

are analyzed in this work. Additionally a Cache

Aware Binary Tree is deﬁned and studied. A cache

aware tree operates by making the tree’s topology cor-

respond with the order in which its nodes are allo-

cated. The goal of a cache aware tree is to ensure

that the descendants of any particular node are more

likely to be located in the same cache line as the node,

thereby leading to higher cache hit rates.

In the experimental stage of this work, a program

is run that constructs and then repeatedly searches a

binary tree. Two key distributions are used to build

and search the tree; the ﬁrst is a uniformly random

set, and the second is a highly nonuniform set of keys.

The number of L1 data cache misses is used as the

metric to evaluate cache performance.

The results demonstrate that for uniform key dis-

tributions, large cache lines do not beneﬁt vanilla or

B. Puzak T. and Huang C. (2006).

AN ANALYSIS OF THE EFFECTS OF SPATIAL LOCALITY ON THE CACHE PERFORMANCE OF BINARY SEARCH TREES.

In Proceedings of the First International Conference on Software and Data Technologies, pages 94-101

DOI: 10.5220/0001315900940101

 SciTePress

AVL trees. Only the cache aware tree, whose nodes

are allocated with cache parameters in mind, experi-

ences fewer cache misses as cache line size increases.

Additionally, results quantitatively show the negative

effects that the AVL tree’s balancing operations have

on spatial locality, while still highlighting the impor-

tance of a short search path. Furthermore, it becomes

clear that the cache aware allocation scheme must

adapt itself to the observed distribution of the input

keys in order to be universally acceptable.

2 RELATED WORK

A function called ccmorph, deﬁned in (Chilimbi et al.,

1999b; Chilimbi et al., 2000) is designed to rearrange

binary trees to make them more cache conscious. The

work shows that by morphing a tree into a cache con-

scious form, the performance of searching the tree

(measured in milliseconds) is improved

In (Bawawy et al., 2001) ccmorph’s performance

in conjunction with software based prefetching was

studied. Additionally, (Hallberg et al., 2003) showed

that cache conscious allocation, particularly with

large cache lines, greatly outweighs the beneﬁts of

hardware or software prefetching.

The effects of different cache associativities on the

cache performance of searching binary trees is studied

in (Fix, 2003).

Efforts to improve the cache performance of Bi-

nary Space Partitioning (BSP) trees through intelli-

gent allocation of nodes within the tree are studied in

(Havran, 2000a; Havran, 1997; Havran, 2000b). The

author demonstrates that by allocating multiple nodes

in a single cache line and then by distributing those

nodes breadth ﬁrst in the growing tree, the running

time of a depth ﬁrst traversal is improved.

A purely empirical analysis on how the sizes and

distributions of input and search keys affects the cache

performance of binary trees was conducted in (Iancu

and Acharya, 2001). In general it was found that bal-

anced trees generally outperformed those that move

nodes to the front, except with search key distribu-

tions that are highly skewed to access only a few keys

repeatedly.

The work in (Oksanen, 1995) provides a means for

predicting the number of cache misses on a particu-

lar search of the tree based on the strategy used to

allocate the tree’s nodes. Additionally, experiments

are conducted to measure the performance improve-

ment of tree accesses (in milliseconds) when cache

conscious allocation strategies are employed.

3 CLASSICAL BINARY TREES

The vanilla tree is the most naive version of a binary

tree. A vanilla tree’s topology is wholly determined

by the insertion order of the keys used to build the

tree. While the expected depth and search complexity

of a vanilla tree is O(lg n) when the tree is built on

a uniformly random input distribution (Cormen et al.,

1998), other distributions carry no such guarantee.

AVL trees (Adelson-Velskii and Landis, 1962;

Weiss, 1999) guarantee O(lg n) depth and search

complexity by adding an invariant to the vanilla tree

requiring that for every node in the tree, the heights

of that node’s left and right subtrees may differ by

at most one. Re-balancing of the tree is performed

through a set of well known operations called AVL

rotations.

4 CACHE AWARE BINARY

TREES

The idea behind a cache aware binary search tree is to

increase the degree of spatial locality exhibited in the

tree’s structure by packing nodes located on a partic-

ular search path into the same cache line.

Nodes in the tree are labeled either used or unused.

When a key is inserted into a cache aware tree, the

standard vanilla protocol is followed with two excep-

tions. First, if the key being inserted lands on an un-

used node then the key is placed into that node and

the node becomes used. Second, if the key falls to a

used leaf node, a block of memory equal to the size of

a cache line is allocated. This block is broken up into

nodes, which are then distributed into the tree accord-

ing to some heuristic.

We deﬁne the term local family to be a group of

nodes that were allocated as a block of memory and

inserted into the tree together. These nodes all reside

in the same cache line.

4.1 Balanced Subtree Ordered Local

Families

In this type of cache aware binary tree (Type I Aware

Trees), local families are distributed into the tree

breadth ﬁrst. All local families in the tree have iden-

tical topologies. Trees built in this fashion favor uni-

form key distributions, because each local family is

of height lg(S

) where S

is the size of a cache

line. Figure 1 illustrates the process of insertion into

a Type I Aware Tree with and without allocation.

In (Havran, 2000a), binary trees are constructed by

packing multiple nodes into a cache line and then ar-

ranging them breadth ﬁrst into a binary tree in order

AN ANALYSIS OF THE EFFECTS OF SPATIAL LOCALITY ON THE CACHE PERFORMANCE OF BINARY

SEARCH TREES

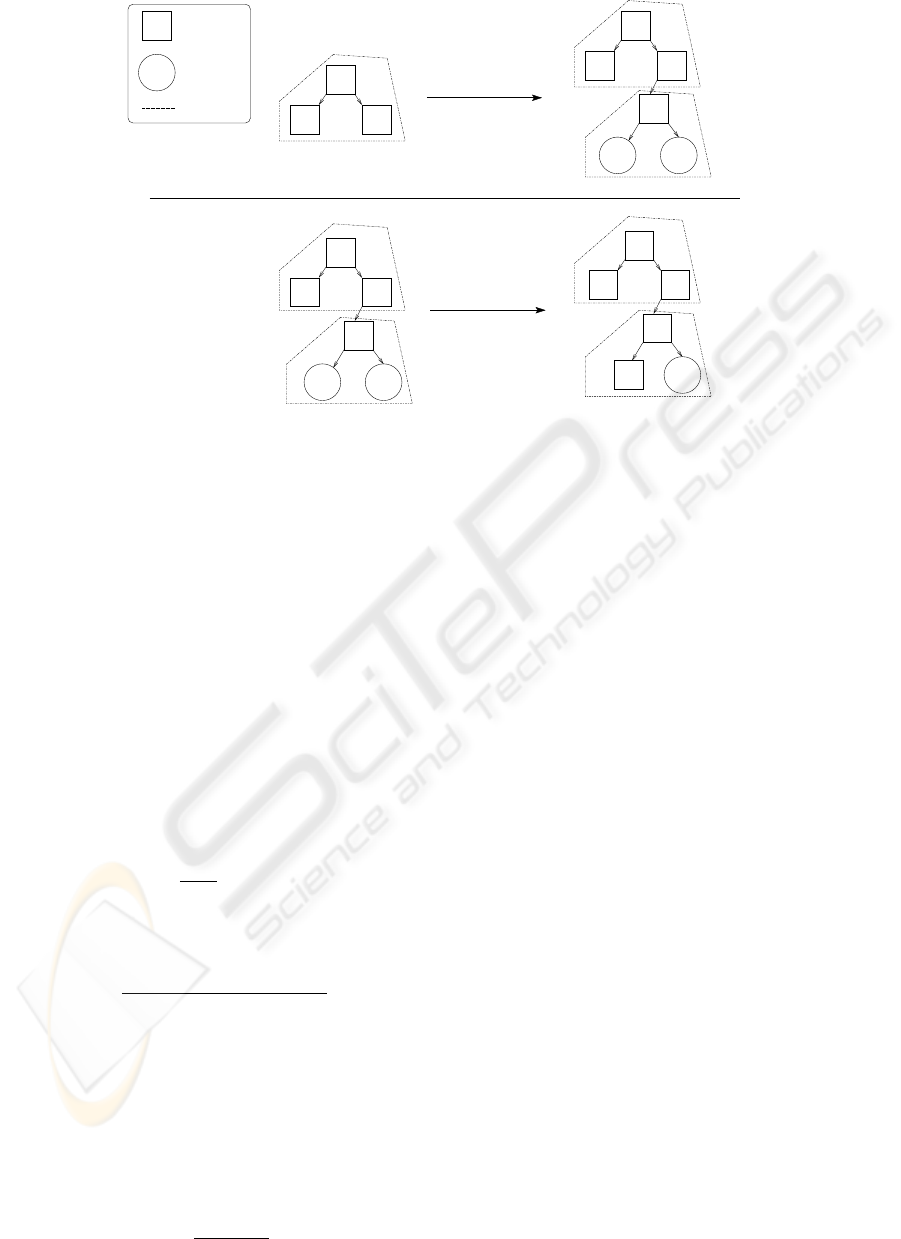
− Used Node

− Unused Node

− Local Family

155

Insert 12

Insert 11

Insertion With Allocation

Insertion Without Allocation

Figure 1: Insertion into a Type I Aware Tree.

to improve the time (CPU cycles) necessary to con-

duct complete depth ﬁrst traversal of the tree. In equa-

tions 1 - 5 we build on this work to determine the ex-

pected number of cache lines accessed when the tree

is searched.

We deﬁne h

to be the height of a complete subtree

or local family. The height of the root node is deﬁned

to be zero. Let S

be the size of a cache line, and

be the size of a node. Then the memory needed

to contain a complete local family in the cache aware

tree is:

M(h

) = (2

− 1)S

≤ S

(1)

From this we derive the complete height of a local

family:

= ⌊(lg(

+ 1)) − 1⌋ (2)

The number of nodes, g

, in the local family with

height greater than h

is then:

= ⌊

− ((2

− 1)S

)

⌋ (3)

Then the average height of the local family h

≥

for g

> 0 is:

= (lg(2

+ g

)) − 1 (4)

For a binary tree of height h

the expected search

depth is d = h

− 1. However, on a search of the tree

we expect to access d + 1 = h

nodes. Therefore the

expected number of local families traversed L

F T

in a

single search of the tree is:

F T

+ 1)

(5)

Since one local family exists in each cache line

F T

is equal to the number of cache lines we can

expect to access on a single search of the tree. This

value can be used to calculate the the average number

of nodes accessed per cache line (see section ??).

One limitation of subtree ordered local families is

that they favor uniform key distributions. The bal-

anced local family topology will have sub-optimal

cache performance in nonuniform situations.

4.2 Insertion Path Ordered Local

Families

Type II Aware Trees are an attempt to make the al-

location of local families closer to optimal by plac-

ing unused nodes according to an approximation of

the observed input key distribution. Nodes in a Type

II Aware Tree contain two additional integer ﬁelds, l

and r, representing the number of keys inserted into

the left and right subtrees of each node respectively.

Insertion into the tree without allocation is performed

exactly as it is in the balanced subtree ordered case,

except that l and r in each node traversed is updated.

When a key is inserted into the tree and alloca-

tion is required, two FIFO lists are used to store the

last q values of l and r that were encountered as the

key traveled down through the nodes of the tree. The

value q can be any positive integer, and reﬂects how

many predecessors of a new local family will be con-

sidered for determining the key distribution approxi-

mation. The contents of the two FIFO lists are used

to compute L =

i=1

and R =

i=1

ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES

The values L and R are used to compute the prob-

abilities of distributing nodes to the left and right in

the newly allocated local family: P (L) =

(L+R)

P (R) =

(L+R)

. When a new local family is allo-

cated, its root is placed in the tree, marked used, and

the key being inserted into the tree is placed in this

node. Then the unused nodes in the local family are

distributed as descendants of the root node according

to P (L) and P (R). The node distribution algorithm

utilizes a biased coin ﬂip where P (L) and P (R) are

the values of heads and tails, respectively.

For local families of size j the probability of the

root node P (n

) = 1. The probabilities of nodes

, i∈[1..j-1] is deﬁned with respect to the root as

P (n

) = P (L)

P (R)

(6)

where g and h are the number of left and right pointers

traversed from n

respectively.

We consider only the last q nodes to determine

P (L) and P (R) so that distant predecessors do not

affect the topology of a new local family.

To determine the likelihood of a local family with

given topology Υ we need to consider the number of

ways that the topology can be constructed Ψ:

Ψ =

(7)

where N is the number of nodes in the tree, and S

a set whose elements consist of the number of nodes

in every subtree of the tree. Then the probability of a

local family with a particular topology Υ is:

P (Υ) = Ψ

(8)

where P

is a set of the probabilities of all of the

nodes in local family, as calculated in equation 6.

Figure 2 illustrates the process of insertion into a

Type II Aware Tree requiring allocation. In this ex-

ample, q = 2 and the size of a local family is 4. It is

important to remember that the newly allocated local

family in Figure 2 is not the only possible topology

that can result from the node distribution method. In

this ﬁgure P (L) =

and P (R) =

, so the topology

depicted in the ﬁgure represents the expected node

distribution.

5 EXPERIMENTAL DESIGN

Experiments are run using the SimpleScalar (Burger

and Austin, 2001) simulation suite. Two rounds of ex-

periments are conducted. The ﬁrst round is designed

to measure detailed metrics about cache performance.

The second round computes metrics on the structure

of a tree which are used to quantify its spatial locality.

In order to measure cache performance metrics a

simple C program is run that builds a binary tree from

the keys in an input ﬁle, and then repeatedly searches

the tree for the keys in a separate ﬁle. The size of

the cache blocks are multiples of 32 bytes, and the

nodes in every tree are exactly 32 bytes. For Type

II Aware Trees the value of q is set to 10. The pro-

gram can run in two modes: build-only or build-

and-search. In build-only mode the program termi-

nates after building the tree, while in build-and-search

mode the program terminates after building the tree

and then searching for all of the keys located in the

search key ﬁle.

5.1 Cache Performance Experiments

For the cache performance experiments the L1 is a 4-

way set associative cache; each run is repeated with

L1 block sizes of 32, 64, 128, and 256 bytes; for each

L1 block size, a run is repeated with L1 cache sizes

of 1, 2, 4, 8, 16, 32, 64, 128, and 256 Kb; the size of

the L2 is always 1024 Kb; the L2 is always a uniﬁed

8-way set associative cache; and all caches utilize the

LRU replacement algorithm. The parameters of the

L2 were chosen so that L2 misses would have a min-

imal impact on the performance of the L1. At the

program’s termination SimpleScalar reports the total

number of L1 data cache misses during execution.

To compute the average number of L1 data cache

misses per search M , we ﬁrst acquire α: the number

of L1 misses taken in build-only mode, and β: the

number of L1 misses taken in build-and-search mode.

On n searches of the tree, M is computed as follows:

M =

(β − α)

(9)

5.2 Tree Structure Experiments

This round of experiments is designed to measure

metrics about searching a binary tree, as well as

to provide insight into the degree of spatial locality

present in the tree. The metrics of interest here are:

the average number of nodes accessed per search, the

average number of cache lines accessed per search,

the average number of nodes accessed per cache line,

and a value for the amount of a cache line that is ﬁlled

with accessed nodes.

To compute the average number of nodes accessed

per search, λ, a global count c of each node encoun-

tered on every search operation is maintained. On n

searches of the tree, the average number of nodes ac-

cessed per search is:

λ =

(10)

To determine the average number of cache lines ac-

cessed per search, γ, the cache line address of each

AN ANALYSIS OF THE EFFECTS OF SPATIAL LOCALITY ON THE CACHE PERFORMANCE OF BINARY

SEARCH TREES

l=0

l=1

r=2

l=0

l=1

r=3

r=1

− Used Node

− Unused Node

− Local Family

L = 1, R = 2

Insert 20

Figure 2: Insertion With Allocation Type II Aware Tree.

node encountered in a search is computed. For each

search the number of unique cache line addresses, u ,

is recorded. For n total searches γ is computed:

γ =

i=1

(11)

The average number of accessed nodes per cache

line, Φ, is simply:

Φ =

(12)

From Φ we derive an expression for the density of

the accessed nodes in a cache line ∆:

∆ = Φ

)

(13)

∆ exists in the range [

, 1] and expresses the

amount of available cache line space that is being uti-

lized by nodes that were accessed.

For Cache Aware Trees the number of unused

nodes in the tree, w, is calculated by a complete depth

ﬁrst traversal of every node (including unused) in the

tree.

5.2.1 Theoretical Bounds

It is possible to bound w and ∆ for Type I Aware

Trees based on the topological structure of a local

family. We deﬁne the number of nodes in a local fam-

ily to be η = ⌊

⌋, and N to be the number of keys

inserted into the tree.

The bounds of these values rely on the average

height of a local family, h

, deﬁned in equation 4.

These local families have identical topologies rep-

resenting approximately balanced trees, hence h

O(lg η). Therefore we can expect to have the great-

est number of unused nodes when only h

+ 1 used

nodes reside in each local family. For N insertions

we will allocate

+1)

local families, each of which

contains η−(h

+1) unused nodes. Multiplying these

quantities we obtain an upper bound for w:

w =

Nη

+ 1)

− N = O(

Nη

lg η

− N ) (14)

To bound ∆ we must realize that regardless of the

key distribution, we can access at most h

+ 1 nodes

in each local family.

∆ =

+ 1)

= O(

lg η

) (15)

For Type II Cache Aware Trees, we can reasonably

expect our biased coin ﬂip to predict the position of

an future key half of the time. Since the root of the

local family is always used we predict

+ 1 used

nodes, and

− 1 unused nodes per local family. The

expected number of unused nodes is:

w = N(

η − 2

η + 2

) = O(N ) (16)

Of course, it is difﬁcult to obtain a strong bound for

w and a bound for ∆ for Type II Aware Trees because

the local families in these trees are not guaranteed to

have identical topologies. Regardless of this short-

coming, we can expect general performance trends

depending on the key distribution. For example, if the

key distribution is uniform, the topologies of the local

families will be balanced, and the values of

w and ∆

approach those of Type I Aware Trees. However, for

nonuniform key distributions, there is the potential for

highly elevated performance. Indeed

w approaches 0

and

∆ approaches 1. This expectation is reﬂected in

the results in section 6.

5.2.2 Type I Aware Tree Predictions

The average height of a local family in a Type I Aware

Tree allows equation 5 to be applied to predict the

values for the tree structure experiments. The predic-

tions are based on modiﬁcations of equations 11 – 13:

ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES

′

, Φ

′

,and ∆

′

= Φ

′

)

. Hence,

the predictions only rely on the direct calculation of λ

from equation 10.

5.3 Key Distribution Details

Each round of experiments is repeated with two key

distributions. The importance of key distributions on

the structure and cache performance of binary trees

was made clear in (Iancu and Acharya, 2001).

The ﬁrst distribution is uniformly random. Trees

are built on an input ﬁle of 1,000,000 keys of which

99,996 are unique, taken from the range [0,99999].

On a duplicate insertion the topology of the tree is not

changed. Using the same distribution on the range [0,

99999] the tree is searched 5,000,000 times.

The second distribution represents a highly nonuni-

form key set. The search keyﬁle consists of 3,118,271

values taken from the instruction addresses of a run-

ning program. Because of their origin, this ﬁle con-

sists of long sequences of increasing numbers. The

ﬁle used to construct the tree, consisting of 174,719

keys, was created from the search key ﬁle by taking

unique keys from the search ﬁle in an order preserving

fashion.

6 EXPERIMENTAL RESULTS

AND ANALYSIS

In the cases with a uniform key distribution, the

vanilla tree and the cache aware trees

had maximum

heights of 44, while the AVL tree had a maximum

height of 20. For the nonuniform distribution, the

vanilla tree and the aware trees had maximum heights

of 1728, while the AVL tree had a maximum height of

21. These values have substantial consequences with

respect to the cache performance of the trees. Because

of space restrictions only tables of representative re-

sults are presented

. In the tables, C refers to cache

size, and B refers to the cache data block size.

For the Vanilla tree built on the uniform key dis-

tribution, the number of misses per search decreases

as cache size increases, but stays the same or slightly

increases as cache line size increases with ﬁxed cache

size. This trend is due to the poor degree of spatial

locality in the Vanilla tree; with 256 byte cache lines

Φ = 1.20. With a nonuniform key distribution how-

ever, large cache lines lead to improved cache perfor-

mance. The highly predictable nature of the nonuni-

form distribution and naive allocation scheme results

Only used nodes are counted in the height of the cache

aware trees.

For complete results please see (Puzak, 2006)

in a natural spatial locality (Φ = 5.91 at 256 byte

lines).

AVL trees had far fewer misses overall than their

Vanilla cousins, but larger cache lines do not con-

tribute to improved performance. See Table 1 for an

example. The observed cache performance is due to

the very low degree of spatial locality present in the

cache aware tree. Indeed, Φ = 1.07 when the key dis-

tribution is uniform, and only 1.14 when it is nonuni-

form.

Somewhat ironically, the AVL tree has the best

cache performance of any tree analyzed when the key

distribution is nonuniform. This is attributable to the

average number of nodes accessed per search λ. With

the nonuniform key distribution λ = 17.05 for AVL

trees and λ = 442.06 for the Vanilla and Cache Aware

Trees. In other words, a typical search of a Vanilla or

Aware tree performs 26 times more memory accesses

than the same search on an AVL tree. More memory

accesses lead to more cache misses.

With the uniform key distribution, the Type I aware

tree takes fewer cache misses per search as both cache

size and cache line size increases. Type II Aware

Trees have performance nearly equal to that of Type I

Aware Trees. See Table 2 for the Type I Aware Tree’s

cache performance results. This performance is at-

tributable to the good degree of spatial locality ob-

served in the cache aware trees. Tables 3 and 4 rep-

resent the predicted and observed values of the tree

structure experiments for the Type I aware trees on

uniform and nonuniform distributions, respectively.

The accuracy of the predictions for the uniform

case suggests that the model is a good approximation

of the physical world. The larger discrepancies in the

nonuniform case exist because we can only expect to

traverse an average of h

+ 1 nodes per local family

if the key distribution is uniform.

On the nonuniform key distribution, the number of

misses per search for the Type I Aware Tree improves

as cache size increases. However, with ﬁxed cache

size more cache misses are observed as cache line size

increases from 32 to 64 bytes. Increases in line size

beyond 64 bytes lead to modest decreases in cache

misses. This observation is explained by the nature of

the nonuniform input distribution. In this case, most

new keys are inserted to the right, but the node distri-

bution algorithm favors placing nodes to the left ﬁrst.

Therefore, with 64 byte cache lines, unused nodes al-

most never become used.

Type II Aware Trees enjoy elevated cache perfor-

mance as both cache size, and cache line size in-

creases regardless of the input distribution. See Ta-

ble 5 for the results from the nonuniform distribution.

The good cache performance of the Type II Aware

tree, regardless of its key distribution, is due to its

high level of spatial locality. The results of the tree

structure experiments for the Type II Aware Tree and

AN ANALYSIS OF THE EFFECTS OF SPATIAL LOCALITY ON THE CACHE PERFORMANCE OF BINARY

SEARCH TREES

Table 1: Average Cache Misses Per Search, AVL Tree, Uniform Distribution.

B C=1K C=2K C=4K C=8K C=16K C=32K C=64K C=128 C=256K

32 21 13.98 11.8 10.51 9.24 7.96 6.69 5.44 4.18

64 23.98 16.26 12.77 11.26 9.88 8.59 7.32 6.04 4.73

128 22.72 18.8 14.42 12.12 10.41 9.02 7.71 6.42 5.09

256 20.43 19.53 17.43 12.96 10.94 9.33 7.96 6.66 5.32

Table 2: Average Cache Misses Per Search, Type I Aware Tree, Uniform Distribution.

B C=1K C=2K C=4K C=8K C=16K C=32K C=64K C=128 C=256K

32 36.7 23.19 17 14.33 12.28 10.42 8.7 7 5.3

64 28.66 18.25 11.97 10.05 8.69 7.43 6.27 5.14 4

128 18.99 13.63 8.65 7.15 6.17 5.28 4.49 3.73 2.98

256 13.6 11.42 7.38 5.47 4.74 4.06 3.51 2.97 2.43

Table 3: Predicted and Observed Type I Aware Tree Results, Uniform Distribution.

B λ γ γ

′

Φ Φ

′

∆ ∆

′

32 22.44 22.44 22.44 1.00 1.00 1.00 1.00 0

64 22.44 15.29 14.16 1.47 1.58 0.74 0.79 33410

128 22.44 10.16 9.66 2.21 2.32 0.55 0.58 77820

256 22.44 7.53 7.08 2.98 3.16 0.37 0.40 155676

Table 4: Predicted and Observed Type I Aware Tree Results, Nonuniform Distribution.

B λ γ γ

′

Φ Φ

′

∆ ∆

′

32 442.06 442.06 442.06 1.00 1.00 1.00 1.00 0

64 442.06 436.11 278.90 1.01 1.59 0.51 0.80 164411

128 442.06 220.17 190.38 2.01 2.32 0.50 0.58 174037

256 442.06 147.34 139.45 3.00 3.17 0.38 0.40 291169

Table 5: Average Cache Misses Per Search, Type II Aware Tree, Nonuniform Distribution.

B C=1K C=2K C=4K C=8K C=16K C=32K C=64K C=128 C=256K

32 1085.63 1059.21 1000.74 883.72 699.66 391.9 88.51 5.77 0.89

64 553.99 540.2 510.51 455.25 357.35 204.67 51.31 6.57 0.47

128 284.37 277.43 264.13 237.32 187.42 108.81 25.93 2 0.34

256 149.34 146.69 140.21 126.74 101.46 62.78 18.11 0.26 0.26

ICSOFT 2006 - INTERNATIONAL CONFERENCE ON SOFTWARE AND DATA TECHNOLOGIES

100

the nonuniform input distribution is provided in Ta-

ble 6. In addition to high degrees of spatial local-

Table 6: Tree Structure Results, Type II Aware Tree,

Nonuniform Distribution.

B λ γ Φ ∆ w

32 442.06 442.06 1.00 1.00 0

64 442.06 227.35 1.94 0.97 5023

128 442.06 118.9 3.72 0.93 15377

256 442.06 64.16 6.89 0.86 35577

ity regardless of the input distribution, Type II Aware

Trees waste only about 12% of the nodes wasted by

Type I Aware Trees. Consideration of these obser-

vations suggests that adaptive cache aware allocation

schemes are superior to methods that are biased to a

particular key distribution.

7 CONCLUSIONS

It is impossible to ignore the importance of a short

search depth, so a balanced binary tree should always

be among the ﬁrst choice of a programmer regardless

of the expected key distribution. However, if a uni-

form key distribution is expected and the target archi-

tecture is built around large cache lines, then a cache

aware tree would be an excellent choice as search

depth would not be much greater than the ideal lg n

and the cache performance will be highly elevated.

For nonuniform inputs, it seems much better to uti-

lize a balanced tree because search depth becomes a

major limiting factor. If the cache is made up of very

many large lines, a good alternative may be a Type II

Aware Tree because it will be able to attain high levels

of cache performance despite the nonuniform nature

of the keys.

On the uniform key distribution, the cache perfor-

mance of the trees is ranked as follows: Type I Aware

Tree, Type II Aware Tree, AVL Tree, Vanilla Tree.

On the nonuniform key distribution, the cache per-

formance of the trees is ranked: AVL Tree, Type II

Aware Tree, Type I Aware Tree, Vanilla Tree.

REFERENCES

Adelson-Velskii, G. and Landis, E. (1962). An algo-

rithm for the organization of information. Doklady

Akademii Nauk SSSR. English translation by Myron J.

Ricci in Soviet Math.

Bawawy, A., Aggarwal, A., Yeung, D., and Tseng, C.

(2001). Evaluating the impact of memory system per-

formance on software prefetching and locality opti-

mizations. In 15th Annual Conference on Supercom-

puting, page 486.

Bryant, R. and O’Hallaron, D. (2001). Computer Systems:

A Programmer’s Perspective. Prentice Hall Inc, New

Jersey.

Burger, D. and Austin, T. (2001). The SimpleScalar Tool

Set, Version 2.0. SimpleScalar LLC.

Chilimbi, T., Davidson, B., , and Larus, J. (1999a). Cache-

conscious structure deﬁnition. In SIGPLAN ’99 Con-

ference on Programming Languages Design and Im-

plementation (PLDI 99).

Chilimbi, T., Hill, M., and Larus, J. (1999b). Cache-

conscious structure layout. In SIGPLAN ’99 Confer-

ence on Programming Languages Design and Imple-

mentation (PLDI 99).

Chilimbi, T., Hill, M. D., and Larus., J. R. (2000). Making

pointer-based data structures cache conscious. Com-

puter Magazine, 33(12):67.

Cormen, T., Leiserson, C., and Rivest, R. L. (1998). Intor-

duction to Algorithms. The MIT Press.

Fix, J. (2003). The set-associative cache performance of

search trees. In Fourteenth Annual ACM-SIAM Sym-

posium on Discrete Algorithms, page 565.

Hallberg, J., Palm, T., and Brorsson, M. (2003). Cache-

conscious allocation of pointer-based data structures

revisited with hw/sw prefetching. In Second Annual

Workshop on Duplicating, Deconstructing, and De-

bunking(WDDD).

Havran, V. (1997). Cache sensitive representation for bsp

trees. In Computergraphics 97, International Confer-

ence on Computer Graphics, page 369.

Havran, V. (2000a). Analysis of cache sensitive representa-

tion for binary space partitioning trees. Informatica,

23(2):203.

Havran, V. (2000b). Heuristic Ray Shooting Algorithms.

PhD thesis, Czech Technical University.

Iancu, C. and Acharya, A. (2001). An evaluation of search

tree techniques in the presence of caches. In 2001

IEEE International Symposium on Performance Anal-

ysis of Systems and Software.

Oksanen, K. (1995). Memory reference locality in binary

search trees. Master’s thesis, Helsinki University of

Technology.

Puzak, T. B. (2006). The effects of spatial locality on the

cache performance of binary search trees. Master’s

thesis, The University of Connecticut.

Sleator, D. and Tarjan, R. (1985). Self adjusting binary

search trees. Journal ACM, 32:652.

Weiss, M. (1999). Data Structures and Algorithm Analysis

in JAVA. Addison-Wesley Longman Inc.

AN ANALYSIS OF THE EFFECTS OF SPATIAL LOCALITY ON THE CACHE PERFORMANCE OF BINARY

SEARCH TREES

101