
AN ENERGY-BASED BACKGROUND MODELLING
ALGORITHM FOR MOTION DETECTION
Paolo Spagnolo, Marco Leo, Tiziana D’Orazio, Andrea Caroppo and Tommaso Martiriggiano
National Research Council – Institute of Intelligent Systems for Automation
Keywords: Motion detection, Background subtraction, Background modeling.
Abstract: Detecting moving objects is very important in many application contexts such as people detection, visual
surveillance, automatic generation of video effects, and so on. The first and fundamental step of all motion
detection algorithms is the background modeling. The goal of the methodology here proposed is to create a
background model substantially independent from each hypothesis about the training phase, as the presence
of moving persons, moving background objects, and changing (sudden or gradual) light conditions. We
propose an unsupervised approach that combines the results of temporal analysis of pixel intensity with a
sliding window procedure to preserve the model from the presence of foreground moving objects during the
building phase. Moreover, a multilayered approach has been implemented to handle small movements in
background objects. The algorithm has been tested in many different contexts, such as a soccer stadium, a
parking area, a street, a beach. Finally, it has been tested even on the CAVIAR 2005 dataset.
1 INTRODUCTION
Many computer vision tasks require robust
segmentation of foreground objects from dynamic
scenes. The most used algorithms for moving
objects detection are based on background
subtraction; for these approaches, the first and
crucial step of these kind of algorithms is the
background creation. Usually, independently from
the applicative context, the main features that each
background modeling algorithm has to handle are:
• Presence of foreground and/or moving
background objects during the model
building phase;
• Gradual and/or sudden variations in
illumination conditions.
Many authors have dealt with the problem of
background modeling, as both a stand-alone task or
a module in a complete motion detection system.
A first group of algorithms uses statistical
approaches to model background pixels. In
(Wren,1997 and Kanade,1998) a pixel-wise gaussian
distribution was assumed to model the background.
In (Wren,1997) the algorithm was used for an indoor
motion detection system, whereas in (Kanade,1998)
the authors tested the algorithm in outdoor contexts.
However, the presence of foreground objects during
the building phase could cause the creation of an
unreliable model, such as in presence of light
movements in the background objects, or sudden
light changes. These observations suggest that
probably the proposed algorithms work well in
presence of a supervised training, during which ideal
conditions are granted by the human interaction. The
natural evolution of these approaches was proposed
in (Stauffer,1999): in this work a generalized
mixture of gaussians was used to model complex
non-static background. In this way the great
drawback of the moving background objects was
solved. However, the presence of foreground objects
during this phase could heavily alter the reliability of
the model, like happened under sudden light
changes. In (Haritaoglu,1998) the authors did not
construct a real gaussian distribution, while they
preferred to maintain general statistics for each
point. In this way they cope with the movements in
background objects, even if they waive a correct
segmentation of foreground objects in those regions.
However, they could encounter misdetections in
presence of foreground objects during the modeling
phase, and in presence of sudden light changes,
while they correctly handle gradual illumination
changes. The natural improvement of this approach
was proposed in (Kim,2004): the basic idea of
(Haritaoglu,1998) was iterated in order to build a
378
Spagnolo P., Leo M., D’Orazio T., Caroppo A. and Martiriggiano T. (2006).
AN ENERGY-BASED BACKGROUND MODELLING ALGORITHM FOR MOTION DETECTION.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 378-383
DOI: 10.5220/0001221403780383
Copyright
c
SciTePress

codebook for each point, providing a set of different
possible values for each point; the experimental
results proposed by the authors appeared interesting.
All the approaches above examined use statistical
information, at different complexity level, for the
background modeling.
A different category is composed by the
approaches that use filters for temporal analysis. In
(Koller,2004) authors used a Kalman-filter approach
for modeling the state dynamics for a given pixel. In
(Elgammal,2000) a non-parametric technique was
developed for estimating background probabilities at
each pixel from many recent samples over time
using Kernel density estimation. In (Doretto,2003)
an autoregressive model was proposed to capture the
properties of dynamics scenes. An improvement of
this algorithm was implemented in (Monnet,2003)
and (Zhong,2003) to address the modelling of
dynamic backgrounds and perform foreground
detection. In (Toyama,1999) a modified version of
the Kalman filter, the Weiner filter, was used
directly on the data. The common assumption of
these techniques was that the observation time series
were independent at each pixel.
All the approaches above presented were tested
on real sequences, producing interesting results,
even if each of them suffered in almost one of the
critical situations listed above. The approaches that
apparently were able to work well in every
conditions implicitly required a supervised
background model construction, in order to prevent,
for example, sudden light changes, or incoming
foreground objects. Moreover, it should be noted
that a modeling algorithm needs to limit the memory
requirements: in an ideal case the best model could
be created by observing a-posteriori all the frames of
the training phase; however this solution is not
reasonable, so one of the constraints of this kind of
algorithms is to work in an incrementally mode, to
reduce hardware requirements.
In this work we present a background modeling
algorithm able to face all the crucial situations
typical of a motion detection system with an
unsupervised approach; no assumptions about the
presence/absence of foreground objects and changes
in light conditions were required. The main idea is to
exploit the pixels energy information in order to
distinguish static points from moving ones. To make
the system more reliable and robust, this procedure
has been integrated in a sliding windows approach,
that is incrementally maintained during the training
phase; in this way the presence of sudden light
changes and foreground objects is correctly handled,
and they do not alter the final background model. In
order to cope with the presence of moving
background objects, a multilayered modeling
approach has been implemented, integrating the one-
layer information given by the previous step with
other data deriving from a long term temporal
analysis. It should be noted that the whole procedure
is on-line: no interaction with user is required at
runtime; user should only opportunely set some
thresholds, as explained in the following sections.
2 ENERGY INFORMATION
One of the main problems of background modeling
algorithm is their sensitiveness to the presence of
moving foreground objects in the scene.
The proposed algorithm exploits the temporal
analysis of the energy of each point, evaluated by
means of sliding temporal windows. The basic idea
is to analyze in a small temporal window the energy
information for each point: the statistical values
relative to slow energy points are used for the
background model, while they are discarded for high
energy ones. In the current temporal window, a point
with a small amount of energy is a static point, that
is a point whose intensity value is substantially
unchanged in the entire window; otherwise it
corresponds to a non static point, in particular it
could be a foreground point or a moving background
one. At this level, these two different cases will be
treated similarly, while in the next section a more
complex multilayer approach will be introduced in
order to correctly distinguish between them.
A coarse-to-fine approach for the background
modeling is applied in a sliding window of size W
(number of frames). The first image of each window
is the coarse background model B
C
(x,y). In order to
create at runtime the required model, instead of
building the model at the end of a training period, as
proposed in (Lipton,2002), the mean (1) and
standard deviation (2) are evaluated at each frame;
then, the energy content of each point is evaluated
over the whole sliding window, to distinguish real
background points from the other ones. Formally,
for each frame the algorithm evaluates mean μ and
standard deviation σ, as proposed in (Kanade,1998):
1
)1(),(),(
−
−+=
ttt
yxyx
μααμμ
(1)
1
)1(|),(),(|),(
−
−+−=
tttt
yxyxyx
σαμμασ
(2)
only if the intensity value of that point is
substantially unchanged with respect to the coarse
background model, that is:
AN ENERGY-BASED BACKGROUND MODELLING ALGORITHM FOR MOTION DETECTION
379

thyxByxI
C
t
<− ),(),(
(3)
where th is a threshold experimentally selected. At
the end of the analysis if the first W frames, for each
point the algorithm evaluates the energy content as
follows:
2
),(),(),(
∫
∈
−=
Wt
C
t
yxByxIyxE
(4)
The first fine model of the background B
F
is
generated as
⎩
⎨
⎧
>
<
=
)(),(
)(),()),(),,((
),(
WthyxEif
WthyxEifyxyx
yxB
F
φ
σμ
(5)
A low energy content means that the considered
point is a static one and the corresponding statistics
are included in the background model, whereas high
energy points, corresponding to foreground or
moving background objects cannot contribute to the
model. The whole procedure is iterated on another
sequence of W frames, starting from the frame W+1.
The coarse model of the background is now the
frame W+1, and the new statistical values (1) and
(2) are evaluated for each point, like as the new
energy content (4). The relevant difference with (5)
is that now the new statistical parameters are
averaged with the previous values, if they already
exist; otherwise, they become the new statistical
background model values. Formally, the new
formulation of (5) become:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≠∧<
−+
=∧
<
=
)(),(
),()(),(
)),(),,((*)1(),(*
),(
)(),()),(),,((
),(
WthyxEif
yxBWthyxEif
yxyxyxB
yxB
WthyxEifyxyx
y
xB
F
F
F
F
φ
φ
σμββ
φ
σμ
(6)
The parameter β is the classic updating parameter
introduced in several works on background
subtraction (Wren,1997), (Kanade,1998) and
(Haritaoglu,1998). It allows to update the existent
background model to the new light conditions in the
scene. The whole procedure is iterated N times,
where N could be a predefined value experimentally
selected to ensure the complete coverage of all
pixels. Otherwise, to make the system less
dependent from any a-priori assumption, a dynamic
termination criteria is introduced and easily verified;
the modeling procedure stops when a great number
of background points have meaningful values:
0)),((#
≅
=
φ
yxB
F
(7)
3 MULTILAYER ANALYSIS
The approach described above allows the creation of
a statistical model for each point of the image, even
if covered by moving objects. However, it is not able
to distinguish movements of the background objects
(for example, a tree blowing in the wind) from
foreground objects. So, the resulting model is very
sensitive to the presence of small movements in the
background objects, and this is a crucial problem,
especially in outdoor contexts.
The solution we propose uses a temporal analysis
of the training phase in order to automatically learn
if the detected movement is due to the presence of a
foreground or a moving background object. The
starting point is the observation that, if a foreground
object appears in the scene, the variation in the pixel
intensity levels is unpredictable, without any logic
and/or temporal meaning. Otherwise, in presence of
a moving background object, there will be many
variations of approximately the same magnitude,
even if these variations will not have a fixed period
(this automatically excludes the possibility to use
frequency-based approaches, i.e. Fourier analysis).
In order to motivate this assumption, we have
analysed the mean intensity values of some points
belonging to different image regions over a long
observation period. The first group is composed by
static background points (zone A in the first image
of fig. 1), while the second (B) is composed by
moving background points (background points that
sometimes are covered by a moving tree). The third
group (C) corresponds to some static adjacent
background points that are covered by both moving
people and a moving tree. Finally, the last region (D)
corresponds to a region covered by only foreground
objects. We have chosen to select a group of points
for each class instead of a single point to reduce the
effects of noise; on the other hand, for each group,
the selected points are very spatially closed, because
of their intensity values need to be similar for a
correct analysis of their temporal trend. Indeed, the
values assumed by each point in the same group
have been averaged, and in figure 1 the temporal
trend of each group of that zones is plotted.
The static points (first graph) assume values that
can be considered constant over the entire
observation period (apart from the natural light
changes). Points corresponding to static background
ICINCO 2006 - ROBOTICS AND AUTOMATION
380
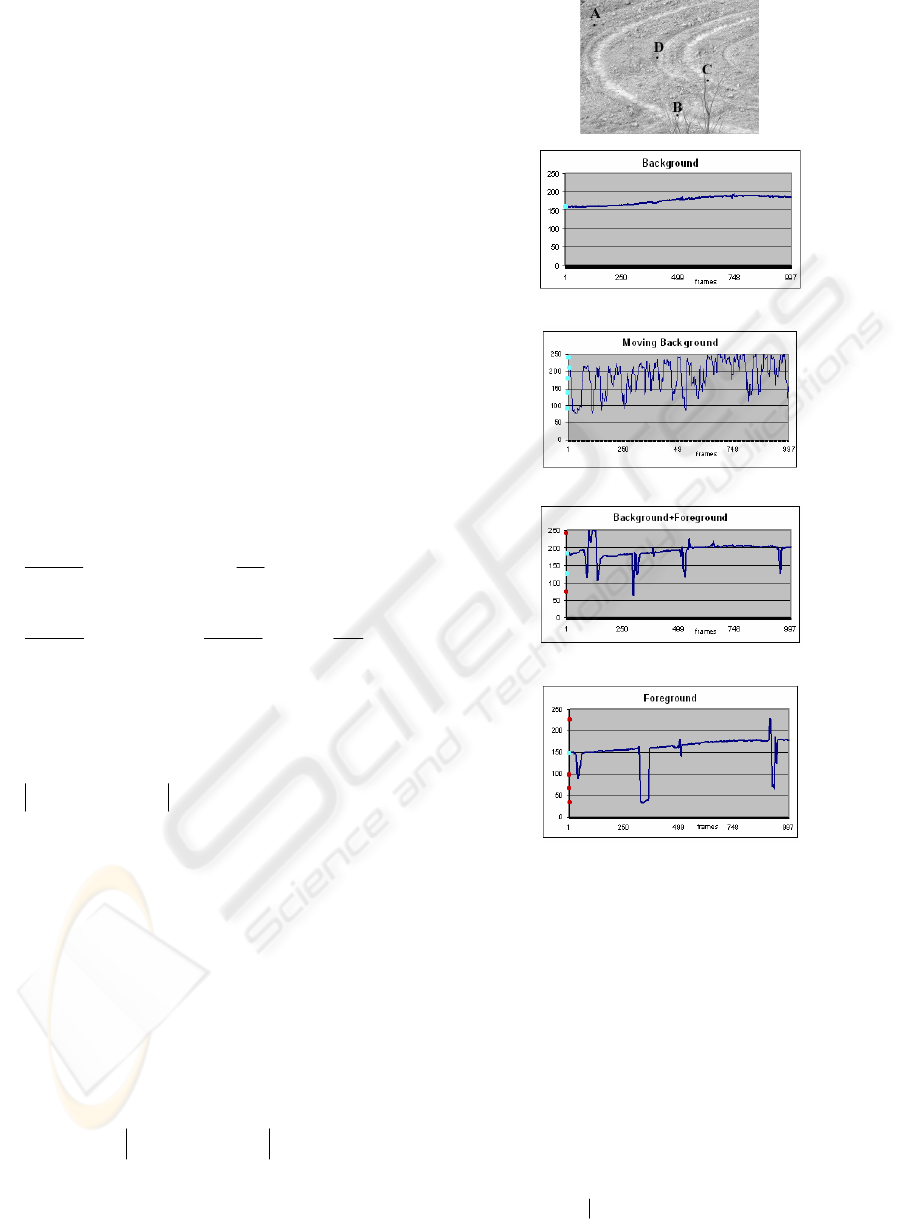
(last graph), but covered by a foreground object (in
this case, a person moving in the scene) assume
values that differs from the standard background
value in an unpredictable way. On the other hand,
static points that sometimes are covered by moving
background objects (second graph) assume values
that return many times in the whole observation
period, even if they have not a fixed frequency. In
the third graph the trend of a background point
covered by both moving background objects and
foreground ones is represented. Some values are
admissible since they return several times, while
some others are occasional so they can be discarded.
Starting from this assumption, the goal of this
step is to use a multilayer approach for the
modelling, with the aim of discarding layers that
correspond to variation exhibited only a few times
for a given point. On the other hand, layers that
return more times will be taken (they correspond to
static points covered by background moving
objects). Formally, the main idea proposed in the
previous section remain unchanged, but it is now
applied to all the background layers. The mean and
standard deviation proposed in (1) and (2) become:
1
)1(),(),(
−
−+=
t
i
t
i
t
i
yxyx
μααμμ
(8)
1
)1(|),(),(|),(
−
−+−=
t
i
t
i
t
i
t
i
yxyxyx
σαμμασ
(9)
where i changes in the range [1…K], and K is the
total number of layers. Similarly, for each frame of
the examined sequence, the decision rule proposed
in (3) for the updating of the parameters becomes:
thyxByxI
i
C
t
<− ),(),(
(10)
where the notation i indicates the examined layer.
It should be noted that, initially, there is only one
layer for each point, the coarse background model
(that correspond to the first frame). Starting from
frame #2, if the condition (10) is not verified, a new
layer is created. At the end of the observation period,
for each point the algorithm builds a statistical
model given by a serious of couple (μ,
σ
) for each
layer. The criteria for selecting or discarding these
values is based again on the evaluation of the energy
content, but now the equation (4) is evaluated for
each layer i:
2
),(),(),(
∫
∈
−=
Wt
i
C
ti
yxByxIyxE
(11)
Region A
Region B
Region C
Region D
Figure 1: the position of the examined regions in the
whole image (first line) and the trend observed in these
regions. Red points correspond to layers that do not
belong to the correct model, while blue points
correspond to correct background layers.
Different layers are created only for those values
that occur a certain number of times in the
observation period. However, in this way both
foreground objects and moving background ones
contribute to the layer creation. In order to
distinguish these two different cases, and maintain
only information about moving background objects,
the overall occurrence is evaluated for each layer:
ilayertheofstatistics
thetoscontributethatyxWyxO
i
),(#),( =
(12)
AN ENERGY-BASED BACKGROUND MODELLING ALGORITHM FOR MOTION DETECTION
381

O
i
(x,y) counts the number of sliding windows that
contributes to the creation of the statistic values for
the layer i. At this point, the first K layers with the
highest overall occurrences belong to the
background model, while the others are discarded.
After the examination of all the points with (12), the
background model contains only information about
the static background and moving background
objects, while layers corresponding to spot noise or
foreground objects are discarded since they occur
only in a small number of sliding windows. The use
of sliding windows allows to greatly reduce the
memory requirements; the trade-off between
goodness and hardware requirements seems to be
very interesting with respect to the others proposed
in (Lipton,2002).
4 EXPERIMENTAL RESULTS
We have tested the proposed algorithm on different
sequences, in different conditions, in both indoor
and outdoor environments. In table 1 the
characteristics of each test sequence are reported.
Some sequences present in the CAVIAR dataset
(http://groups.inf.ed.ac.uk/vision/CAVIAR/CAVIA
RDATA1) have also been considered. Each
sequence represents a different real situation, and
different frame rates demonstrate the relative
independency from the size of the sliding window
(in our experiments, we have chosen to use a sliding
window containing 100 frames, independently from
the context and the camera frame rate).
Table 1: Characteristics of the test sequences.
Test Sequence Context Frame rate Size
Archeological site
Outdoor
30 768X576
Laboratory Indoor 30 532X512
Museum Indoor 15 640X480
Soccer stadium Outdoor 200 1600X600
Beach Outdoor 20 720X576
CAVIAR seq. 1 Outdoor 25 384X288
CAVIAR seq. 2 Indoor 40 384X288
The first tests were carried out to evaluate the
number of layers necessary for a given situation. In
the second column of table 2 the mean number of
layers for each context is proved. As it can be seen,
this value is smaller for more structured contexts
(laboratory, museum, soccer stadium), while it is
higher in generic outdoor contexts (archeological
site, CAVIAR seq. 1). The maximum number of
layer in our experiments has been fixed to 5. The
presence of moving trees in the background in the
two contexts of the beach and the archeological site
increases the number of layers. In more controlled
environments, like the laboratory, requiring a small
number of layer, probably the multilayer approach
can be considered unnecessary.
In order to have a quantitative representation of
the reliability of the background models, we have
chosen to test them by using a standard, consolidated
motion detection algorithm, proposed in
(Kanade,1998). A point will be considered as a
foreground point if it differs from the mean value
more than two times the standard deviation; in order
to adapt this rule to our multilayer approach, we
consider a point as a moving point the previous
assert is valid for at least one layer:
),(2),(),( yxyxyxI
ii
σμ
∗>−
(13)
A quantitative estimation of the error,
characterized by the Detection Rate (DR) and the
False Alarm Rate (FAR), has been used as suggested
in (Jaraba,2003):
F
N
T
P
TP
DR
+
=
F
P
T
P
FP
FAR
+
=
(14)
where TP (true positive) are the detected regions that
correspond to moving objects; FP (false positive) are
the detected regions that do not correspond to a
moving object; and FN (false negative) are moving
objects not detected.
Table 2: The mean number of layers and rates to measure
the confidence for each of the examined different contexts.
Test sequence
Mean number
of layers
DR
(%)
FAR
(%)
Archeological site
3.12
87,46 3,72
Laboratory
1.23
93,81 4,16
Museum
2.05
89,12 4,83
Soccer stadium
1.92
94,31 2,26
Beach 4.33 88,56 5,26
CAVIAR seq. 1 2.28 89,18 3,24
CAVIAR seq. 2 1.54 91,15 3,85
In the last two columns of table 2 we can see that
the FAR parameter is always under the 6%, and it is
higher for more complex environments (i.e. beach,
museum), while it assumes small values in more
controlled contexts (i.e. soccer stadium).
Starting from the detection rule proposed in (13),
we have chosen to use the perturbation detection rate
(PDR) analysis to validate our approach. This
technique, as explained in (Chalidabhongse,2003),
makes the experimental results less sensitive to the
effects of a manual ground truth segmentation. The
goal of the PDR analysis is to measure the detection
sensitivity of a background subtraction algorithm
ICINCO 2006 - ROBOTICS AND AUTOMATION
382
without assuming knowledge of the actual
foreground distribution. This analysis is performed
by shifting or perturbing the entire background
distributions by values with fixed magnitude Δ, and
computing an average detection rate as a function of
contrast Δ. More details about this procedure can be
found in relative paper. The PDR analysis has been
applied to all the experimental contexts presented
above. The test set is given by 500 points for each
frame, 200 frames for each sequence in each
context. So, for each Δ, 200*500 perturbations and
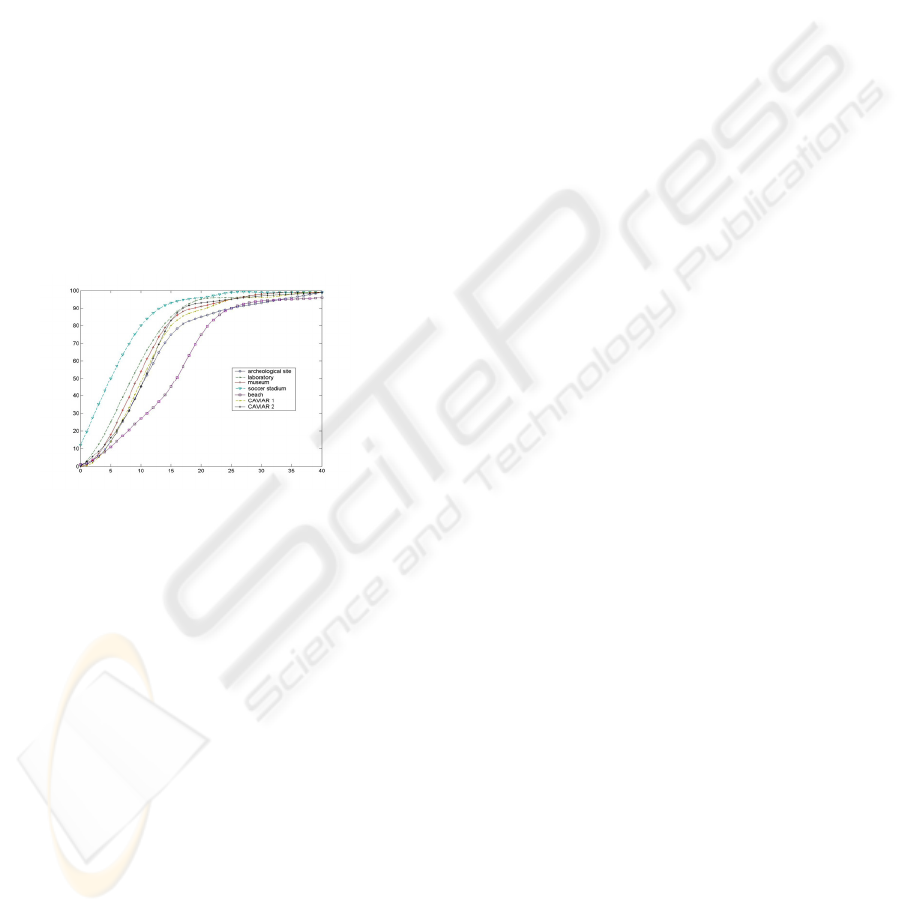
detection tests were performed. In figure 2 we have
plotted the resulting PDR graphs. The worst results
have been obtained in the beach, where the critical
conditions due to the presence of moving
background objects decrease the performance. In
this case, the pixel intensity variations, due to the
movement of the vegetation, are amplified by the
perturbation introduced, causing a decrease of the
global detection ability. On the other hand, the
results obtained in the remaining contexts are very
interesting, with a fast growth of the curve towards
best performances, as already observed in table 2.
Figure 2: the PDR analysis on the test sequences. It can
be note that the best performance have been obtained in
the soccer stadium and in the indoor contexts, while the
worst results have been reported in the beach, probably
due to the presence of moving vegetations.
5 CONCLUSIONS
In this paper an approach for the unsupervised
building of a background model has been proposed.
The proposed algorithm is able to model a scene
even in presence of foreground objects and moving
background ones; no a-priori assumptions about the
presence of these moving objects, and changing in
light conditions are needed. It combines the energy
information of each pixel with a temporal analysis of
the scene, by means of sliding windows, to detect
static background points. Energy information is used
again over the whole observation period to
distinguish moving background objects from
foreground ones, and the background is modeled by
means of a multilayer statistical distribution.
The algorithm has been tested in many different
contexts, such as a soccer stadium, a parking area,
an archeological site and two test sequences
extracted from the CAVIAR 2005 dataset. The
experimental results prove that the proposed
algorithm try to correctly model the background in
every kind of condition, in presence of both moving
background and foreground objects. The quantitative
evaluation presented confirm that the proposed
algorithm gives reliable results.
REFERENCES
Chalidabhongse, T.H., Kim, K., Harwood, D., Davis, L.S.,
2003. A Perturbation Method for Evaluating
Background Subtraction Algorithms, Proc. VS-PETS.
Doretto, G., Chiuso, A., Wu, Y.N., Soatto, S., 2003.
Dynamic textures. In IJCV, 51 (2), pp 91-109
Elgammal, A., Harwood, D., Davis, L.S., 2000. Non-
parametric model for background subtraction. In
ECCV, Vol. 2, pp. 751-767
Haritaoglu, I. ,Harwood, D., Davis, L.S., 1998. Ghost: A
human body part labeling system using silhouettes. In
Fourteenth ICPR, Brisbane.
Jaraba, E.H., Urunuela,C., Senar,J., 2003. Detected motion
classification with a double-background and a
Neighborhood-based difference, PRL, (24),pp.2079-
82.
Kanade, T., Collins, T., Lipton, A., 1998. Advances in
Cooperative Multi-Sensor Video Surveillance. Darpa
Image Und. Work., Morgan Kaufmann,pp.3-24.
Kim, K, Chalidabhongse, T.H., Harwood, D., Davis, L.,
2004. Background modeling and subtraction by
codebook construction. Proc. ICIP, Vol. 5, pp 3061–
64
Koller, D., Weber, J., Malik, J., 1994. Robust multiple car
tracking with occlusion reasoning. In ECCV pp 189-96
Lipton, A.J., Haering, N., 2002. ComMode: an algorithm
for video background modeling and object
segmentation. Proc. of ICARCV, pp 1603-08, vol.3
Monnet, A., Mittal, A., Paragios, N., Ramesh, V., 2003.
Background modelling and subtraction of dynamic
scenes. In ICCV, pp. 1305-12
Stauffer, C., Grimson, W., 1999. Adaptive background
mixture models for real-time tracking. In CVPR, pp
246-252
Toyama, K., Krumm, J., Brumitt, B., Meyers, B., 1999.
Wallflower: Principles and practice of background
maintenance. In ICCV, pp. 255-261
Wren, C.R. Azarbayejani, A., Darrell, T., Pentland, A.P.,
1997. Pfinder: real-time tracking of human body.
IEEE Trans. PAMI, 19(7), pp. 780 – 785.
Zhong, J., Sclaroff, S., 2003. Segmenting foreground
objects from a dynamic, textured background via a
robust kalman filter. In ICCV, pp.44-50
AN ENERGY-BASED BACKGROUND MODELLING ALGORITHM FOR MOTION DETECTION
383
