
PREEMPTIVE SCHEDULING IN A TWO-STAGE
MULTIPROCESSOR FLOWSHOP WITH RESOURCE
CONSTRAINTS
Ewa Figielska
Warsaw School of Computer Science
Lewartowskiego 17, 00-169 Warsaw, Poland
Keywords:
Two-stage flowshop, Parallel machines, Resource constraints, Column generation algorithm, Genetic algo-
rithm.
Abstract:
A heuristic combining the column generation technique and a genetic algorithm is proposed for solving the
problem of preemptive scheduling in a two-stage flowshop with parallel unrelated machines and renewable re-
sources at the first stage and a single machine at the second stage. The objective is to minimize the makespan.
The lower bound on the optimal makespan is derived to be used in the performance analysis of the heuris-
tic. The performance of the heuristic is analyzed by a computational experiment. The results show that the
heuristic is able to find near-optimal solutions in reasonable computation time.
1 INTRODUCTION
This paper proposes a heuristic combining the col-
umn generation (CG) technique with a genetic algo-
rithm (GA) for solving the multiprocessor flowshop
scheduling problem which can be briefly described as
follows: there are a number of preemptive jobs to be
processed at two stages, each job being processed first
at stage 1 then at stage 2. Stage 1 consists of a num-
ber of parallel unrelated machines, at stage 2 there is
a single machine. Upon completion at stage 1 a job is
ready to be processed at stage 2: it may be processed
at stage 2 when the machine is available there, or it
may reside in a buffer space of unlimited capacity fol-
lowing stage 1 until the machine at stage 2 becomes
available. At stage 1, a job can be processed on any of
the parallel machines, and its processing times may be
different on different machines. The processing of a
job on a machine of stage 1 may be interrupted at any
moment and resumed later on the same or another ma-
chine. A job during its processing at stage 1 requires
some amounts of additional renewable resources. The
total amounts of these resources available at any mo-
ment are limited.
The objective is to find a feasible schedule which
minimizes the maximum job completion time in the
two-stage flowshop, C
max
, referred to as makespan.
This problem is NP-hard in the strong sense since
the problem of preemptive scheduling in the two-
stage flowshop with two identical parallel machines
at one stage and one machine at another is NP-hard in
the strong sense (Hoogeveen et al., 1996).
During the last decade the flowshops with multi-
ple machines (FSMP), also called hybrid flowshops,
received considerable attention from researchers.
Most literature in this area addresses the minimum
makespan problems under the assumption that pre-
emptions of jobs are not allowed and the parallel ma-
chines at each stage are identical, e.g. (Gupta, 1988;
Chen, 1995; Haouari and M’Hallah, 1997; Brah and
Loo, 1999; Linn and Zhang, 1999; Oguz et al., 2003).
Only few papers concern the flowshop with parallel
machines that are not identical (Suresh, 1997; Ruiz
and Maroto, 2006).
To the best of our knowledge the multiproces-
sor flowshop scheduling problem with additional re-
source constraints has not been considered in the lit-
erature so far.
In this study, two-stage multiprocessor flowshop
scheduling research is extended by considering the
preemptive scheduling of unrelated parallel machines
with additional resource constraints. Such a problem
may arise in real-life systems that are encountered in
a variety of industries, e.g. in chemical, food and cos-
metics industries. These systems are often subjected
to some additional resource constraints for example
on the availability of the additional resources such as
skilled labor, tools, power. Preemption of jobs usu-
130
Figielska E. (2006).
PREEMPTIVE SCHEDULING IN A TWO-STAGE MULTIPROCESSOR FLOWSHOP WITH RESOURCE CONSTRAINTS.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 130-135
DOI: 10.5220/0001220101300135
Copyright
c
SciTePress
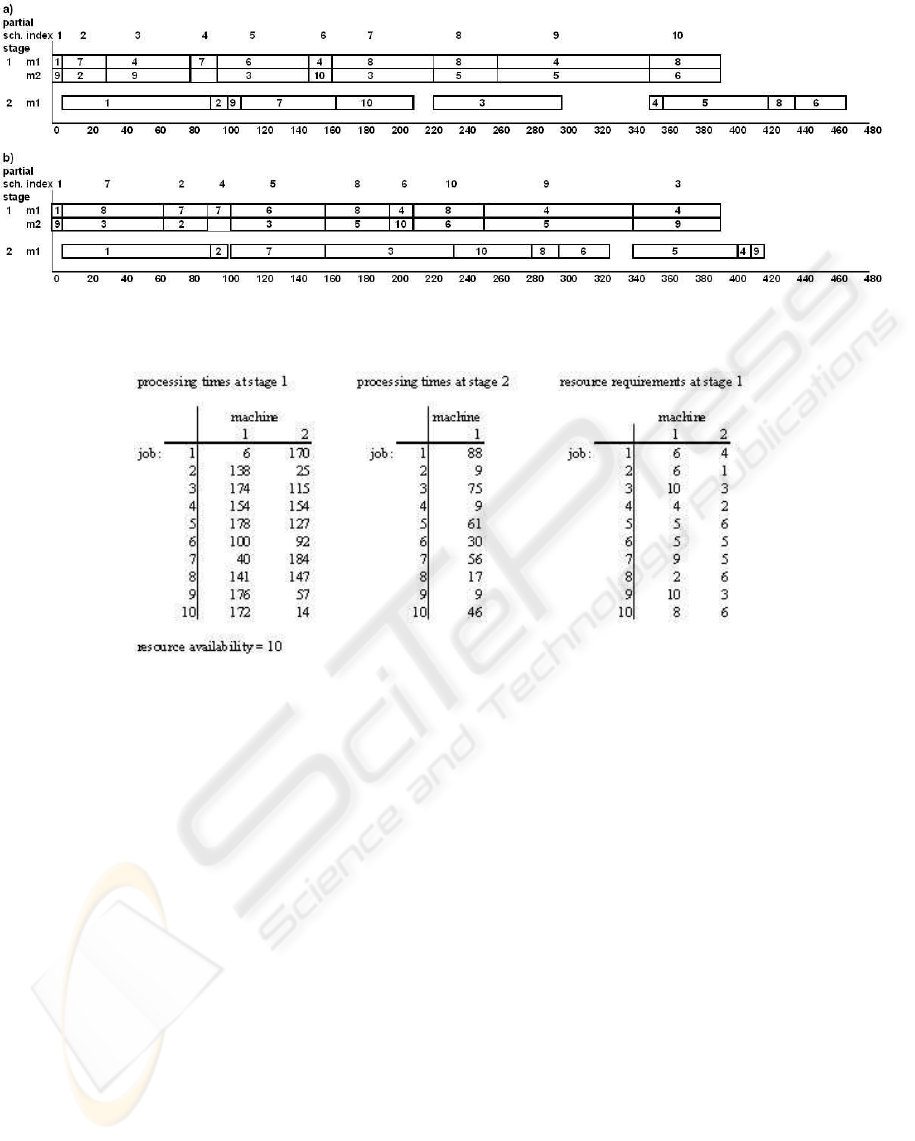
Figure 1: An illustrative example. The resulting schedules: a) the feasible schedule with a random sequence of the partial
schedules, b) the final schedule with the sequence of the partial schedules minimizing the makespan.
Figure 2: The data for an illustrative example.
ally results in shortening a schedule. The problem
with parallel unrelated machines at the first stage and
a single machine at the second stage may arise in a
manufacturing environment in which products are ini-
tially processed on any of parallel machines and then
each product must go through a final testing opera-
tion, which is to be carried out on a common testing
machine.
2 THE FRAMEWORK OF THE
HEURISTIC
The proposed heuristic proceeds in two steps.
Step 1. A column generation algorithm solves the
minimum makespan problem of unrelated par-
allel machines scheduling with additional re-
source constraints which occurs at stage 1.
The solution is composed of a number of par-
tial schedules and its makespan does not de-
pend on the ordering of the partial schedules.
A partial schedule assigns some jobs (or parts
of jobs) to machines for simultaneous process-
ing during a certain period of time, so that
resource constraints are fulfilled at every mo-
ment.
Step 2. A genetic algorithm finds the sequence of the
partial schedules that minimizes the makespan
in the two-stage flowshop which is equal to the
maximum job completion time at stage 2. For
each sequence of the partial schedules gen-
erated in the search process the completion
times of jobs at stage 1 are calculated. Then,
a schedule for the two-stage flowshop is con-
structed and its makespan is calculated taking
into account the job ready times (equal to the
job completion times at stage 1) and process-
ing times of jobs at stage 2.
To illustrate the performance of the heuristic we
present the following example. Consider an instance
of 10 jobs with the job processing times, resource re-
quirements and resource availability as shown in Fig-
ure 2. There are two stages: stage 1 contains two
parallel unrelated machines, stage 2 consists of one
PREEMPTIVE SCHEDULING IN A TWO-STAGE MULTIPROCESSOR FLOWSHOP WITH RESOURCE
CONSTRAINTS
131

machine. Figure 1 presents two schedules for this in-
stance. Each schedule in the two-stage flowshop may
be treated as composed of a schedule of the first stage
and a schedule of the second stage. The schedules of
the first stage parallel machines are composed of 10
partial schedules. Each partial schedule satisfies re-
source constraints at a time. The availability of the
resource at any moment is 10 units. For example, in
the partial schedule of index 1, S
1
, job 1 and job 9 re-
quire, respectively, 6 and 3 units (see Figure 2) of the
resource at a time, so the total usage of the resource at
any moment in this partial schedule is equal to 9 and
is no greater than 10. Similarly, all remaining partial
schedules satisfy resource constraints at any moment.
In Figure 1a the sequence of the partial schedules
is S
1
, S
2
, S
3
, S
4
, S
5
, S
6
, S
7
, S
8
, S
9
, S
10
. We can
see that for this sequence of the partial schedules, the
first job completed at stage 1 is job 1 (it is finished
in S
1
). After completing at stage 1, job 1 starts on
the machine at stage 2 because this machine is free.
The next job completed at stage 1 (in S
2
) is the job
of index 2. After its completion job 2 is stored in the
buffer space between the stages until the machine of
stage 2 is freed up. The indices of successive jobs
completed at stage 1 are: 1, 2, 9, 7, 10, 3, 4, 5, 8,
6. In Figure 1a, we observe that the machine at stage
2 remains idle after finishing processing jobs 10 and
3 when it waits for the completion of jobs 3 and 4,
respectively, at stage 1.
In Figure 1b the sequence of the partial schedules is
S
1
, S
7
, S
2
, S
4
, S
5
, S
8
, S
6
, S
10
, S
9
, S
3
. This sequence
has been found by the GA so as to minimize the max-
imum job completion time at stage 2 (the makespan
of the whole schedule). For this sequence of the par-
tial schedules, jobs are completed at stage 1 in the
following order: 1, 2, 7, 3, 10, 8, 6, 5, 4, 9, and their
completion times are different than those in Figure 1a,
which results in a much smaller idle time of the sec-
ond stage machine and a much shorter schedule then
those in Figure 1a.
3 NOTATION
In this paper jobs are indexed by j, parallel machines
at stage 1 by i, resource types by r. The parameters
of the problem considered are as follows:
n the number of jobs,
m the number of machines at stage 1,
l the number of types of renewable resources,
p
ij
the processing time of job j on machine i at
stage 1,
s
j
the processing time of job j on the machine at
stage 2,
W
r
the number of units of resource r available at a
time,
α
ijr
the number of units of resource r required at
every moment during processing job j on ma-
chine i at stage 1.
4 HEURISTIC DESCRIPTION
4.1 Solving the Problem of Stage 1
As stated in Section 2, first, the problem of resource
constrained preemptive scheduling of parallel unre-
lated machines so as to minimize the makespan is
solved. The solution to this problem is represented
by a set S of partial schedules S
β
, β ∈ B, where B
is the set of indices of all feasible partial schedules.
Partial schedule is determined by its duration ∆
β
and
the values of v
β
ij
(i = 1 . . . m,j = 1 . . . n) represent-
ing an assignment of jobs to machines, where v
β
ij
= 1
if job j is processed on machine i in partial schedule
S
β
and v
β
ij
= 0, otherwise. The problem is formally
defined as follows:
min
X
β∈B
∆
β
(1)
subject to:
X
β∈B
∆
β
m
X
i=1
v
β
ij
p
ij
= 1, j = 1, . . . , n (2)
n
X
j=1
v
β
ij
≤ 1, i = 1, . . . , m, β ∈ B (3)
m
X
i=1
v
β
ij
≤ 1, j = 1, . . . , n, β ∈ B (4)
m
X
i=1
n
X
j=1
α
ijr
v
β
ij
≤ W
r
, r = 1, . . . , l, β ∈ B (5)
v
β
ij
∈ {0, 1}, i = 1, . . . , m, j = 1, . . . , n, β ∈ B
(6)
∆
β
≥ 0, β ∈ B (7)
where ∆
β
(β ∈ B) and v
β
ij
(i = 1, . . . , m, j =
1, . . . , n, β ∈ B) are decision variables. Constraints
(2) ensure that all jobs are completed at stage 1 of the
two-stage flowshop. Constraints (3) and (4) ensure
that, respectively, each machine works on at most one
job at a time and each job is processed on no more
than one machine at a time. Due to constraints (5)
the usage of each resource at every moment does not
exceed its availability.
In the general case, the above problem is known
to be NP-complete (Slowinski, 1980). It can be opti-
mally solved by means of a CG algorithm. The theo-
retical basis of the CG technique has been provided by
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
132

Dantzig and Wolfe in (Dantzig and Wolfe, 1960) (for
applications of the CG technique see e.g. (Gilmore
and Gomory, 1961; Barnhart et al., 1998; Figielska,
1999; Chen and Lee, 2002)).
A CG algorithm does not generate explicitly all
columns of the problem, which correspond to all par-
tial schedules. It works only with a subset of columns
and adds a new column which improves the solution.
At each iteration of the CG algorithm, the schedule
length is minimized by solving the LP problem of the
form:
min
X
β∈
˜
B
∆
β
(8)
subject to:
X
β∈
˜
B
∆
β
m
X
i=1
v
β
ij
p
ij
= 1, j = 1, . . . , n (9)
∆
β
≥ 0, β ∈
˜
B (10)
where β ⊂
˜
B denotes a subset of indices of columns,
∆
β
(β ∈
˜
B) are decision variables, and the values of
v
β
ij
(i = 1, . . . , m, j = 1, . . . , n, β ∈
˜
B) are fixed
(determined in the previous iterations) or (before the
first iteration) given in advance. Let π
∗
j
(j = 1, . . . , n)
be the optimal solution of the dual problem to the
problem (8)-(10) (π
∗
j
are dual variables corresponding
to constraints (9)). If there exists a column β ∈ B \
˜
B
such that
P
n
j=1
P
m
i=1
π
∗
j
v
β
ij
pij
− 1 > 0, then the current
set
˜
B can be extended by this new index β and a new
iteration of the CG algorithm is started. Otherwise,
the optimal solution is found and the algorithm stops.
4.2 Finding the Schedule of Minimal
Makespan
The aim is the minimization of the makespan in the
two-stage flowshop. A GA finds the ordering of the
partial schedules which provides the schedule for the
two-stage flowshop with minimum makespan.
A GA (Holland, 1975) is a search technique that
imitates the natural selection and biological evolu-
tionary process. GAs have been used in a wide vari-
ety of applications, particularly in combinatorial opti-
mization problems and they were proved to be able to
provide near optimal solutions in reasonable time.
A GA starts with a population of randomly gen-
erated candidate solutions (called chromosomes). A
chromosome is represented by a string of numbers
called genes. Each chromosome in the population is
evaluated according to some fitness measure. Certain
pairs of chromosomes (parents) are selected on the
basis of their fitness. Each of these pairs combines
to produce new chromosomes (offspring) and some
of the offspring are randomly modified. A new pop-
ulation is then formed replacing some of the original
population by an identical number of offspring. The
process is repeated until a stopping criterion is met.
Let P (t) denotes the population at iteration t and
pop
size is the population size. The GA applied in
this paper can be outlined as follows.
1. Generate and evaluate the initial population P (t),
t = 0.
2. Repeat the following steps until stopping condition
is satisfied.
2.1. Repeat the following loop
pop size
2
times
(pop
size is an even number).
2.1.1. Select two parents from P (t).
2.1.2. Apply the crossover operator over the
parent chromosomes and produce 2
offspring chromosomes.
2.1.3. Apply the mutation operator over the
offspring.
2.1.4. Copy the offspring to population P (t+
1).
2.2. Evaluate P (t + 1).
2.3. Replace the worst chromosome of P (t+1) by
the best chromosome found so far.
2.4. Set t = t + 1.
3. Return the best chromosome found.
The factors which characterize the GA applied to
the problem considered in this paper are determined
as follows.
Solution representation. A solution to the sequenc-
ing problem solved by the GA is coded as a single
chromosome whose genes represent the indices of
partial schedules.
Initial population. An initial population of chro-
mosomes is randomly generated.
Evaluation. The value of an objective function,
which is equal to the makespan in the two-stage flow-
shop, is used to measure the fitness of a chromo-
some. For each partial schedule sequence (chro-
mosome) generated in the search process, a sched-
ule for the two-stage flowshop is constructed and
the makespan is calculated taking into account ready
times and processing times of jobs at stage 2.
Parent selection. The binary tournament selection
method is used. In a binary tournament selection,
two chromosomes are randomly chosen. The more fit
(with a smaller objective function value) is then taken
as a parent chromosome. Two binary tournaments are
held to produce two parents.
Crossover. The two-point crossover operator PMX
(Goldberg, 1989) is applied to each pair of par-
ent chromosomes with a probability P
crs
(crossover
probability).
Mutation. The genes of each chromosome in the
population are considered one by one, and the gene
being considered swaps its value with another ran-
PREEMPTIVE SCHEDULING IN A TWO-STAGE MULTIPROCESSOR FLOWSHOP WITH RESOURCE
CONSTRAINTS
133

domly generated gene of the same chromosome with
a probability P
mut
(mutation probability).
Stopping condition. The search process terminates
when the best objective function value (makespan)
found so far is not updated for a predetermined num-
ber of iterations.
On the basis of the preliminary computational ex-
periment the following values of the genetic parame-
ters which ensure a good performance of the algo-
rithm were selected: pop
size = 30, P
crs
= 0.8,
P
mut
= 0.01, the number of iterations without any
improvement of the best solution found so far is set at
250.
5 LOWER BOUND
Since determination of the optimal solution to the
considered problem is practically impossible (for
larger size problems it is impossible even in the case
of flowshop with identical parallel machines and no
resource constraints (Santos et al., 1995)), a simple
and easily computable lower bound on the optimal
makespan is derived to evaluate the quality of the pro-
posed heuristic.
Let C
∗
CG
denotes the minimal makespan (i.e. the
minimum time needed to complete all jobs at stage 1)
for the problem occurring at stage 1. The first lower
bound on the optimal makespan in the two-stage flow-
shop is obtained from the following equation:
LB
1
= C
∗
CG
+ min
j=1,...,n
{s
j
} (11)
The second term of the above equation represents the
minimum unavoidable idleness at stage 1 which is
equal to the smallest job processing time at stage 2.
The second lower bound is given by:
LB
2
= min
i=1,...,m,j=1,...,n
{p
ij
} +
n
X
j=1
s
j
(12)
since the machine at stage 2 remains idle for at least
the time needed to complete at stage 1 a job with the
smallest processing time at stage 1.
LB
1
and LB
2
will be effective for problem in-
stances which are dominated by jobs with large
processing times at stage 1 and stage 2, respectively.
Hence, a lower bound on the optimal makespan in
the considered two-stage flowshop will be
LB = max{LB
1
, LB
2
} (13)
6 COMPUTATIONAL
EXPERIMENT
In this section the results of a computational exper-
iment conducted to evaluate the performance of the
Table 1: The computational results.
n m δ (%) CPU time (s)
CG alg GA
20 2 1.16 0.67 0.14
3 2.48 1.46 0.13
4 1.73 1.83 0.16
40 2 0.50 2.01 0.59
3 0.45 4.38 0.52
4 0.61 3.84 0.48
60 2 0.29 4.56 1.00
3 0.37 8.36 1.23
4 0.69 7.21 1.33
80 2 0.19 7.66 1.95
3 0.45 12.96 2.71
4 0.24 12.66 2.59
100 2 0.07 12.29 3.82
3 0.15 21.20 4.45
4 0.22 17.48 5.15
120 2 0.08 18.71 6.20
3 0.18 31.05 9.14
4 0.19 27.54 7.05
average: 0.56 10.88 2.70
proposed heuristic are presented. 360 randomly gen-
erated instances were created and examined. In-
stances were generated for the number of jobs n =
20, 40, 60, 80, 100 and 120, the number of machines
at stage 1, m = 2, 3 and 4, and one resource type.
Resource requirements, α
ijr
, were generated from
U[1, 10] (U [a, b] denotes the discrete uniform distri-
bution in the range of [a, b]), whereas the resource
availability, W
1
, was set at 10. Processing times at
stage 1, p
ij
, were generated from U[1, 200], U [1, 250]
and U[1, 300] for instances with 2, 3 and 4 machines,
respectively, whereas processing times at stage 2, s
j
,
were generated from U[1, 100] for all instances.
To evaluate the performance of the proposed
heuristic two performance measures are used. The
first is the relative deviation of a heuristic solution
from the lower bound on the optimal makespan (in
other words the maximum relative deviation from the
optimal makespan) defined as
δ =
C − LB
LB
× 100%,
where C is the best makespan found by the heuristic.
The second performance measure is the CPU time (re-
ported in seconds) consumed by the heuristic to find
the best solution.
The results of the experiment are presented in Ta-
ble 1. The first two columns show the size of the in-
stances. The relative deviation is presented in column
3. Columns 4 and 5 contain the CPU time (in seconds)
consumed by the CG algorithm and the GA, respec-
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
134

tively. The entries in Table 1 are average values over
20 instances.
The results show that the presented heuristic per-
forms very well for the entire collection of instances.
We observe that δ decreases with the increase in the
number of jobs. On average δ = 1.79%, 0.52%,
0.45%, 0.29%, 0.15% and 0.15% for problems with
20, 40, 60, 80, 100, and 120 jobs, respectively. The
CPU time of the heuristic grows with the number of
jobs. This increase is more significant for the CG al-
gorithm than for the GA. The number of machines
does not seem to affect significantly the computation
time of the heuristic, however, we observe that in the
case of 2 machines the CG algorithm consumes less
CPU seconds than in the cases of 3 and 4 machines.
7 CONCLUSIONS
In this paper a heuristic combining the column gener-
ation algorithm with the genetic algorithm for solving
the two-stage flowshop preemptive scheduling prob-
lem with parallel unrelated machines and resource
constraints at the first stage, and a single machine at
the second stage has been developed. The heuristic
has been tested as to its effectiveness in finding a min-
imum makespan schedule and as to its computation
time. The obtained results indicate that for problems
with a large number of jobs the heuristic usually finds
schedules with makespan close to the optimal value
in reasonable computation time.
REFERENCES
Barnhart, C., Johnson, E., Nemhauser, G., Savelsbergh, M.,
and Vance, P. (1998). Branch and price: column gen-
eration for solving huge integer problems. Oper. Res.,
46:316–329.
Brah, S. A. and Loo, L. L. (1999). Heuristics for scheduling
in a flow shop with multiple processors. Europ. J. of
Opernl Res., 113:113–112.
Chen, B. (1995). Analysis of classes of heuristics for
scheduling a two-stage flow shop with parallel ma-
chines at one stage. J. of Opernl Res. Soc., 46:234–
244.
Chen, Z.-L. and Lee, C.-Y. (2002). Parallel machine
scheduling with a common due window. Europ. J. of
Opernl Res., 136:512–527.
Dantzig, G. B. and Wolfe, P. (1960). Decomposition prin-
ciple for linear programs. Oper. Res., 8:101–111.
Figielska, E. (1999). Preemptive scheduling with
changeovers: using column generation technique and
genetic algorithm. Comp. and Ind. Engin., 37:63–66.
Gilmore, P. C. and Gomory, R. E. (1961). A linear program-
ming approach to the cutting-stock problem. Oper.
Res., 9:849–859.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-
timization and Machine Learning. Addison-Wesley.
Gupta, J. N. D. (1988). Two stage hybrid flowshop schedul-
ing problem. J. of Opernl Res. Soc., 39:359–364.
Haouari, M. and M’Hallah, R. (1997). Heuristic algorithms
for the two-stage hybrid flowshop problem. Oper. Res.
Let., 21:43–53.
Holland, J. H. (1975). Adaptation in Natural and Artificial
Systems. University of Michigan Press, Ann Arbor,
MI.
Hoogeveen, J. A., Lenstra, J. K., and Veltman, B. (1996).
Preemptive scheduling in a two-stage multiproces-
sor flow shop is np-hard. Europ. J. of Opernl Res.,
89:172–175.
Linn, R. and Zhang, W. (1999). Hybrid flow shop schedul-
ing: a survey. Comp. and Ind. Engin., 37:57–61.
Oguz, C., Ercan, M. F., Cheng, T. C. E., and Fung, Y. F.
(2003). Heuristic algorithms for multiprocessor task
scheduling in a two-stage hybrid flow shop. Europ. J.
of Opernl Res., 149:390–403.
Ruiz, R. and Maroto, C. (2006). A genetic algorithm for hy-
brid flowshops with sequence dependent setup times
and machine eligibility. Europ. J. of Opernl Res.,
169:781–800.
Santos, D. L., Hunsucker, J. L., and Deal, D. E. (1995).
Global lower bounds for flow shop with multiple
processors. Europ. J. of Opernl Res., 80:112–120.
Slowinski, R. (1980). Two aproaches to problems of re-
source allocation among project activities - a compar-
ative study. J. Opl Res. Soc., 31:711–723.
Suresh, V. (1997). A note on scheduling of two-stage flow
shop with multiple processors. Int. J. of Prod. Econ.,
49:77–82.
PREEMPTIVE SCHEDULING IN A TWO-STAGE MULTIPROCESSOR FLOWSHOP WITH RESOURCE
CONSTRAINTS
135
