
HYBRID LEARNING METHOD FOR DISCRETE
MANUFACTURING CONTROL
USING KNOWLEDGE BASED MODEL
Ewa Dudek
Institute of Automatics, AGH University of Science and Technology
Mickiewicza 30, 30-059 Krakow, Poland
Tadeusz Dyduch
Institute of Computer Science, AGH University of Science and Technology
Mickiewicza 30, 30-059 Krakow, Poland
Keywords:
Control, knowledge acquisition, knowledge representation, learning system, discrete manufacturing process.
Abstract:
The aim of the paper is to present a conception of a hybrid learning method for discrete manufacturing
processes control.The method is based on a special form of a knowledge based model of discrete manufactur-
ing process, named here hybrid knowledge based model (HKBM). The model consists of two parts, each of a
different type of model: algebraic-logical model in a state spacethat is created on a basis of process technology
description and set of expert rules referring to control. A general scheme of HKBM of a vast class of discrete
manufacturing processes (DMP) is given in the paper. Then the method of synthesis of intelligent, learning
algorithms that use information on the process gained in previous iterations as well as an expert knowledge is
described. To illustrate the presented ideas, the scheduling algorithm for a special NP-hard problem is given.
1 INTRODUCTION
The paper deals with a learning based method applied
to control of discrete manufacturing process. A lot of
different learning methods have been developed (Ci-
chosz, 2000). They are suitable for application aims
and character of available pieces of information. The
conception of a learning method, however, depends
most essentially on knowledge representation (KR)
method utilised for a learning process. This paper
presents conception of a learning method based on
a hybrid knowledge representation model. Recently,
a lot of investigations referring to knowledge based
control method are carried out because models and
knowledge about controlled processes are the vital
parts of the controlling systems. In the knowledge-
based intelligent process planning systems a signifi-
cant role plays knowledge acquisition. In order to dis-
cover association rules under uncertainty, fuzzy deci-
sion techniques and entropy-based analysis methods
as well as fuzzy clustering integrated with variable
precision rough set are used (Zhonghao et al., 2005).
On the other hand e.g. for autonomous unmanned
vehicle the system is required being able to dynam-
ically construct a knowledge structure representing a
process under control, meeting the constraints associ-
ated with a particular process. The system should be
able to manage and monitor changes in the structure
and derive knowledge about it. Usually process con-
straints are specified with temporal logic formulas and
monitored using appropriate execution monitor (Do-
herty, 2005).
At the same time KR methods for computer aided
manufacturing have been developed (McGuinness
and Patel-Schneider, 1998), (Liebowitz, 1998). They
are vital for information system for manufacturing
management such as MRPII or/and ERPII. Each of
the system contains components so called shop floor
control, especially referring to control of discrete
manufacturing processes and scheduling. However,
there are no proper optimal control algorithms imple-
mented in the components. The implemented algo-
rithms use only simple control rules. On the other
hand a variety of discrete processes have been de-
scribed and their optimisation algorithms have been
presented in the scientific literature. The question
arises: why there are no these optimisation algo-
rithms implemented in information management sys-
tems, produced even by the best computer firms such
as SAP, Oracle or IFS? According to the authors one
of the reasons is lack of common knowledge represen-
tation method for manufacturing processes control.
The paper deals with knowledge based modelling
of discrete manufacturing/production processes and
its applications for manufacturing process planning
algorithms. It presents developing of ideas given in
160
Dudek E. and Dyduch T. (2006).
HYBRID LEARNING METHOD FOR DISCRETE MANUFACTURING CONTROL USING KNOWLEDGE BASED MODEL.
In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 160-166
DOI: 10.5220/0001219201600166
Copyright
c
SciTePress

(Dudek-Dyduch, 2000). Its aim is 3-fold:
– to present a scheme for general, hybrid knowl-
edge based model of a class of discrete manufac-
turing/production processes (DMP),
– to present a learning method based on the hybrid
knowledge based model
– to present learning algorithm for scheduling an ex-
emplary NP-hard problem.
The control of DMP (scheduling DMP) lies in de-
termining a manner of performing some set of jobs
under restrictions referring to machines/devices, re-
sources, energy, time, transportation possibilities, or-
der of operation performing and others. Most of
control algorithms are approximate (heuristic) due to
NP-hardness of the optimisation problems. Within
the frame of artificial intelligence, one attempts both
formal elucidation of heuristic algorithm ideas and
giving some rules for creating them (metaheuristics)
(Dudek-Dyduch and Fuchs-Seliger, 1993), (Dudek-
Dyduch and Dyduch, 1988), (Pearl, 1988), (Rajedran,
1994). The paper is connected with this direction of
the research. It uses formal model based on a special
kind of the multistage decision process enlarged with
an expert knowledge.
2 HYBRID KNOWLEDGE BASED
MODEL OF DMP
In (Dudek-Dyduch, 1990), (Dudek-Dyduch and Dy-
duch, 1992), (Dudek-Dyduch and Dyduch, 1993) the
general scheme of algebraic-logical model of DMP,
that is a special form of knowledge based model,
has been presented. It represents a discrete decision
process jointed with simulation process.Simulation
aimed at scheduling of any DMP consists in deter-
mining a sequence of process states and the related
time instances. The new state and its time instant de-
pend on the previous state and the decision that has
been realised (taken) then. Decision determines the
job to be performed, resources, transport unit etc. The
algebraic-logical model of DDP will be extended to
HKBM. Let’s recall it briefly.
Definition 2.1 A discrete manufacturing/production
process DMP is a process that is defined by the sextu-
ple DMP=
U, S, s
0
, f, S
N
, S
G
where
U is a set of control decisions or control signals,
S = X × T is a set named a set of generalized states,
X is a set of proper states,
T ⊂ R
+
∪ {0} is a subset of non negative real num-
bers representing the time instants,
f : U ×S → S is a partial function called a transition
function, (it has not to be determined for all elements
of the set U × S),
s
0
=
x
0
, t
0
, S
N
⊂ S, S
G
⊂ S are respectively: an
initial generalized state, a set of not admissible gener-
alized states, and a set of goal generalized states, i.e.
the states in which we want the process to take place
at the end.
The transition function is defined by means of two
functions, f = (f
x
, f
t
) where
f
x
: U × X × T → X determines the next state,
f
t
: U × X × T → T determines the next time
instant.
It is assumed that the difference ∆t = f
t
(u, x, t)−t
has a value that is both finite and positive.
Thus, as a result of the decision u that is taken or
realised at the proper state x and the moment t, the
state of the process changes for x
0
= f
x
(u, x, t) that
is observed at the moment t
0
= f
t
(u, x, t) = t + ∆t.
Because not all decisions defined formally make
sense in certain situations, the transition function f
is defined as a partial one. Thanks to it, all limita-
tions concerning the control decisions in a given state
s can be defined in a convenient way by means of so-
called sets of possible decisions U
p
(s), and defined
as: U
p
(s) = {u ∈ U : (u, s) ∈ Dom f }.
At the same time a DMP is represented by a set of
its trajectories that starts from the initial state s
0
. It
is assumed that no state of a trajectory, apart from the
last one, may belong to the set S
N
or has an empty
set of possible decisions. Only a trajectory that ends
in the set of goal states is admissible. The control
sequence determining an admissible trajectory is an
admissible control sequence (decision sequence). The
task of optimisation lies in the fact of finding such an
admissible decision sequence ˜u that would minimize
a certain criterion Q.
In the most general case, sets U and X may be pre-
sented as a cartesian product U = U
1
×U
2
×. . . U
m
,
X = X
1
× X
2
× . . . X
n
i.e. u = (u
1
, u
2
, . . . u
m
),
x = (x
1
, x
2
, . . . , x
n
). There are no limitations im-
posed on the sets, in particular they have not to be nu-
merical ones. Thus values of particular co-ordinates
of a state may be names of elements (symbols) as
well as some objects (e.g. finite set, sequence etc.).
Particular u
i
represent separate decisions that must
or may be taken at the same time. The sets S
N
,
S
F
, and U
p
are formally defined with use of logi-
cal formulae. Therefore, the complete model consti-
tutes a specialised form of a knowledge based model
(logic-algebraic model). According to it’s structure
the knowledge on DMP is represented by coded in-
formation on U, S, s
0
, f , S
N
, S
G
. Function f may
be defined by mean of procedure or by means of rules
of type IF..THEN.
The presented paradigm of knowledge based model
consists of the following main procedures realising
rules IF..THEN, utilizes by control algorithms: proce-
dure that generates and examines subsets of possible
HYBRID LEARNING METHOD FOR DISCRETE MANUFACTURING CONTROL USING KNOWLEDGE BASED
MODEL
161

decisions U
p
(s), procedures that realize the function
f (in the most cases it is a vector function), i.e. deter-
mine the next state (x
0
, t
0
) = f(u, x, t), procedures
that examine if the state belongs to the set S
N
or S
G
.
The basic structure of a fixed DMP (Def.2.1) is usu-
ally created on a basis of process technology descrip-
tion. Basing on additional expert knowledge and/or
analysis of DMP subsets of states can be differenti-
ated, for which best decisions or some decision choice
rules R (control rules) are known. Similarly, some
subsets of advantageous or disadvantageous states for
the controlled process can be determined. Formally,
the knowledge allow us restrict sets of possible deci-
sions U
p
.
Knowledge represented by the basic knowledge
structure DMP (Def.2.1) enriched by expert knowl-
edge create the hybrid knowledge based model
(HKBM) of DMP. The knowledge can be enriched
further additionately as a result of simulation exper-
iments.
Basing on the model of DMP different classes
of algorithms can be formally defined and analysed.
For example in (Dudek-Dyduch and Dyduch, 1992),
(Tadeusiewicz and Dudek-Dyduch, 1998), classes of
branch & bound algorithms for DMP control opti-
misation have been differentiated as well as some
rules of automatic creation of lower bounds have been
given. In the next section application of HKBM of
DMP for intelligent, learning algoritm is presented.
3 SEARCH METHOD WITH
GATHERING INFORMATION
The most popular search algorithms consist in gener-
ating consecutive, possibly better and better, trajecto-
ries. They use a specially created function or local
optimisation task for the choice of the best decision
at each state of the generated trajectory. The crite-
rion for local optimisation is called a preference func-
tion or simply heuristics. In this section we present a
conception of algorithms that gain information on the
process and also use expert knowledge.
In the author’s earlier paper (Dudek-Dyduch and
Fuchs-Seliger, 1993), (Dudek-Dyduch and Dyduch,
1993), a certain general 3-stage method for designing
local optimisation task is proposed. Let us recall it
briefly.
At the first stage, one formulates some conditions
for the optimal (suboptimal) solution. They refer di-
rectly to subsets of decisions, or/and determine the
state sets that are advantageous (or disadvantageous)
from the criterion point of view or for a possibility
of generation of an admissible trajectory. The condi-
tions can result from theoretical analysis of the model
or can be formulated by experts.
At the second stage, one determines a local optimi-
sation task. In order to do it, the information about the
distinguished, at the first stage, advantageous or dis-
advantageous states as well as information on S
G
, S
N
and sets of possible decisions is used. As we need the
generated trajectory to run only through the advanta-
geous states and to avoid the disadvantageous ones, it
seems most natural to introduce any measure of dis-
tance in the state space, and to assume some local
criterions.. It was explained in (Dudek-Dyduch and
Dyduch, 1993) that different semimetrics can be used
as an approximate measures of distance. Basing on
the local change of the global criterion Q and maxi-
mization (minimization) of the mentioned distances,
we obtain the substitute local problem, usually a mul-
ticriteria one.
At the third stage, one should determine the manner
of solving the local multicriteria optimisation task.
The basic ideas of multicriteria decision approach
(Dudek-Dyduch, 1990), (Dudek-Dyduch and Fuchs-
Seliger, 1993), (Vincke, 1992), can be applied here.
For learning algorithms, however, the most useful are
these solving manners that assume priority or weight
coefficients for the particular criterions because these
priorities may be modified during consecutive simu-
lation experiments.
A learning algorithm acquires and gathers a knowl-
edge about the process in the following way. Each
new generated trajectory is analysed. If it is not ad-
missible, the reasons of the failure are examined. For
example, it is examined through which subsets of not
advantageous states the trajectory has passed. A role
of the criterions connected with this subsets should be
strengthened for the next trajectory i.e. the weights
(priorities) of these criterions should increase. When
the generated trajectory is admissible, the role of the
criterions responsible for the trajectory quality can
be strengthened, i.e. their weights can be increased.
Basing on the gained information, the local optimisa-
tion task is being improved during simulation exper-
iments. This process is treated as learning or intel-
ligent searching algorithm. The gathered knowledge
is represented by means of coefficients at particular
components of the criterium. This conception has
been examined and is presented in (Dudek-Dyduch,
2000).
If one posses additional expert knowledge then a
better algorithm can be proposed. If some state sub-
sets S
di
, i = 1, 2, . . . are distinguished and for these
states some rules for decision choice R
i
, i = 1, 2, . . .
are given by an expert then algorithm should verify
additionally to which subset the new generated state
belongs and should realise the suitable rule R
i
. If
rules given by expert excludes some decisions then
the suitable sets of possible decision U
p
(s) are de-
creased.
Another idea of learning algorithm for some
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
162

scheduling problem is given in (Kolish and Drexel,
1995), (Sprecher et al., 1995).
4 SCHEDULING PROBLEM
WITH RETOOLING
DEPENDING ON PROCESS
STATE
To illustrate the application of the presented method,
let us consider the following scheduling problem that
takes place when scheduling preparatory works in
mines.
The set of headings in the mine must be driven
in order to render the exploitation field accessible.
The headings form a net, formally represented by a
nonoriented multigraph G = (I, J, P ) where the set
of branches J and the set of nodes I represent the
set of headings and the set of heading crossings re-
spectively, and relation P ⊂ (I × J × I) determines
connections between the headings (a partial order be-
tween the headings). There are two kinds of driving
machines, that differ in efficiency, cost of driving and
necessity of transport. The first kind machines (set
M1) are more effective but a cost of driving by means
of them is much higher than for the second kind (set
M2). Additionally, the first kind machines must be
transported when driving starts from another head-
ing crossing than the one in which the machine is,
while the second type machines need no transport.
Driving a heading cannot be interrupted before its
completion and can be done only by one machine a
time. There are given due dates for some of the head-
ings. They result from the formerly prepared plan of
fields exploitation. One must determine the order of
heading driving and the machine by means of which
each heading should be driven so that the total cost of
driving be minimal and each of headings be complete
before its due date.
There are given: lengths of the headings, efficiency
of both kinds of machines (driving length per time
unit), cost of a length unit driven for both kinds of
machines, cost of the time unit waiting for both kinds
of machines, speed of machine transport and transport
cost per a length unit.
The problem is NP-hard (Dudek-Dyduch, 2000).
NP-hardness of the problem justifies the application
of approximate (heuristic) algorithms. A role of a
machine transport corresponds to retooling during a
manufacturing process. The time needed for a trans-
port of a machine depends on headings that have been
driven earlier, thus it depends on a process state.
The process state at any instant t is defined as a
vector
x = (x
1
, x
2
, . . . , x
n
), n = |J|.
A coordinate x
j
describes the state of the j-th head-
ing (branch),
x
j
= (m, ∆, i, s) where
m denotes the number of the machine that is as-
signed to the j-th heading,
∆ denotes the time after which the machine will be
accessible,
s is a parameter that defines whether the machine is
driving the heading (s = 1), whether it is transported
in the heading (s = 2) whether it is waiting in one
of the heading ends (the nearest heading crossings)
(s = 3),
i denotes the number of the heading crossing
(node) to which the machine is moving or in which
it is waiting. If there is no machine assigned to the
heading then m = 0 and s = 0.
If the driving of a heading has been not started
yet, then ∆ = ∞ and when it is complete, then
∆ = 0. The initial state x
0
= (0, ∞, 0, 0). For any
state (x, t) one can determine a set of headings that
are being driven (J
1
), the driving of which is com-
plete (J
2
), and not started yet (J
3
). A state (x, t)
belongs to the set of not admissible states if there is
a heading whose driving is not complete yet and its
due date is earlier than t. Formally, S
N
= {(x, t) :
there exists j /∈ J
2
such that d(j) < t} where d(j)
denotes the due date for the j-th heading. A state
(x, t) is a goal if all the headings have been driven,
i.e. S
G
= {(x, t) : ∀j ∈ J, j ∈ J
2
}.
A decision determines the headings that should
be started at the moment t, machines which drive,
machines that should be transported, headings along
which machines are to be transported and ma-
chines that should wait. Thus, the decision u =
(u
1
, u
2
, . . . , u
n
) where the co-ordinate u
j
refers to
the j-th heading and is of the form: u
j
= (m, q). The
symbol m denotes the number of a machine that is as-
signed to the heading. The parameter q ∈ {0, 1, 2, 3}
and denotes respectively: waiting, driving, transport
and withdrawing of the machine. When a machine
m ∈ M1 is in the node i and should drive the k-th
heading that is not adjacent to the i-th node, then the
machine is transported in the nearest way accessible
in the considered state. This way is computed by the
Ford’s algorithm (a polynomial one).
Obviously, not all the pairs (m, q) constitute pos-
sible decisions in the state (x, t). For example, a de-
cision u
j
= (m
k
, 1) is possible only when the j-th
heading is neither being driven nor complete and the
machine m
k
is in the one of the heading crossing ad-
jacent to the j-th heading. The complete definition
of the set of the possible decision U
p
(x, t) will be
omitted here because it is not necessary to explain the
idea of the algorithm. The detailed description of the
formal model for the considered problem is given in
(Dudek-Dyduch, 2000).
HYBRID LEARNING METHOD FOR DISCRETE MANUFACTURING CONTROL USING KNOWLEDGE BASED
MODEL
163
∆
∆
∆
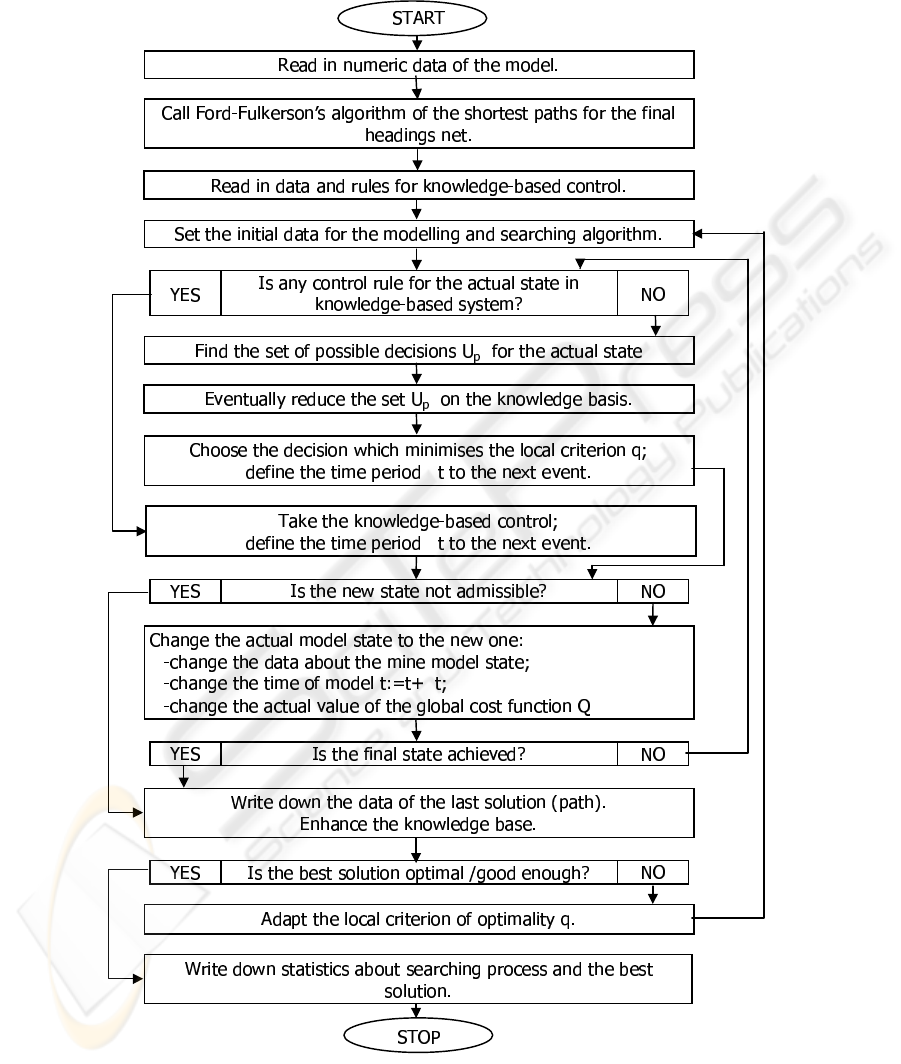
Figure 1: Block-schema of the algorithm.
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
164

5 LEARNING ALGORITHM
The algorithm for the solution of the problem consists
in generating consecutive trajectories. Each of them is
generated with the use of the specially designed local
optimisation task and then is analysed. The informa-
tion gained as a result of the analysis is used in order
to modify the local optimisation task for the next tra-
jectory, i.e. for the next simulation experiment. This
approach is treated as a learning without a teacher.
The construction of the local optimisation criterion
q for the presented example is based on two criterions.
The first one, denoted as q
1
refers to the minimal in-
crement of the global criterion value, computed from
the current to the last state of a generated trajectory.
The second one denoted as q
2
takes into account
that the trajectory should pass possibly far from the
not admissible states, or from the states from which
there is a little chance to accomplish a goal state. Thus
the local criterion q = q
1
+bq
2
, where b is a parameter
that is being changed during simulation experiments.
q
1
= ∆Q(u, x, t) + Q
0
(x
0
, t
0
) (1)
where ∆Q denotes the increment of the global crite-
rion Q during a simulation step, i.e. when the current
state (x, t) is changed, as a result of the decision u,
to the state (x
0
, t
0
) = f(u, x, t). Q
0
(x
0
, t
0
) is a lower
estimation of the global criterion value for the latter
part of the trajectory, i.e. for the part that starts from
the state (x
0
, t
0
). This estimation is equal to the low-
est cost of the driving of the remaining headings when
the limitations referring to the due dates are neglected.
The lowest cost is computed under assumption that
only machines of the second type (set M2) are ap-
plied.
Criterion q
2
takes into account consequences of the
decision u from the due date limitations point of view.
L(x
0
, t
0
) estimates a minimal distance between the
new state (x
0
, t
0
) and the set of not admissible states
S
N
.
q
2
=
1
L(x
0
, t
0
)
(2)
L(x
0
, t
0
) is computed as follows. For the state x
0
, the
set of accessible headings’ crossings is determined,
i.e. the crossings from which driving can be started.
There is also determined the set of headings whose
driving has been not started yet and which have the
due dates. For each of the headings, the shortest time
needed for performing it is computed. It is denoted
as st(j) where j is the number of the heading. The
time is needed for driving all the headings that con-
stitute the shortest way from an accessible heading
crossing and for performing of the considered head-
ing. It is assumed that the driving is performed by
means of the first kind machines (i.e. the more effec-
tive ones) and their transport to the accessible cross-
ing is neglected. Then, for the each of the headings
the difference d(j) − st(j) − t
0
is computed. If any
of the differences has negative value, the generated
trajectory cannot be admissible and is rejected. If all
the differences are nonnegative, L(x
0
, t
0
) is given by
formula:
L(x
0
, t
0
) = min
d(j) − st(j) − t
0
d(j) − t
0
=
= min
1 −
st(j)
d(j) − t
0
(3)
The formula is not applied for the headings that
had been determined earlier on a basis of the expert
knowledge or bottom up analysis. Finally the local
criterion q consists of 3 components:
q = ∆Q(u, x, t) + Q
0
(x
0
, t
0
) + b
1
L(x
0
, t
0
)
(4)
The value of the criterion q is computed for each
u ∈ U
p
(x, t). This decision u
∗
for which the crite-
rion value is minimal is chosen. Then the next state
(x
0
, t
0
) = f(u
∗
, x, t) is generated and the new best
decision u ∈ U
p
(x
0
, t
0
) is chosen. If a newly gener-
ated trajectory is admissible and for most of its states
the distance to the set of not admissible states is rela-
tively big, the parameter b can be decreased. In such a
situation the role of the optimisation compound is en-
larged. On the contrary, when the generated trajectory
is not admissible, the parameter b should be increased
because then the greater emphasis should be put to the
due date limitations.
The presented conception is an essential extension
of the one given in (Dudek-Dyduch, 2000). Com-
puter experiments that have been carried out for the
simpler algorithm are presented in (Dudek-Dyduch,
2000). They confirmed that learning-based approach
is very efficient. Basing on those results one may be
sure that the presented algorithm that use additionally
an expert knowledge will be very efficient too.
6 CONCLUSIONS
The paper presents a conception of intelligent search
method (learning-based algorithms) for scheduling.
A large number of difficult scheduling problems in
manufacturing can be efficiently solved by means of
these method. A basis for the algorithms is a special
kind of hybrid knowledge based model(HKBM) of
discrete manufacturing processes (DMP), that is given
in the paper. The model for a fixed DMP consists
of two parts. The first part corresponds to algebraic-
ligical model in the state space and is created mainly
on a basis of DMP technology description. The sec-
ond part constitutes a set of expert’s rules.
It should be pointed out that the presented hybrid
KR structure is also useful for creating simulation
HYBRID LEARNING METHOD FOR DISCRETE MANUFACTURING CONTROL USING KNOWLEDGE BASED
MODEL
165

packages for a large class of discrete processes be-
cause the special form of the model enables one to
create the simulation package of a modular form.
Such simulation package of a mixed structure,
combining KR and multiagent system can be used for
testing and developing strategies, prepared for crisis
management. To illustrate the conception, the learn-
ing based algorithm for preparatory work in a mine is
presented.
ACKNOWLEDGEMENTS
The research was supported in part by grant No 3
T11C 025 27 from Polish Committee of Scientific Re-
search.
REFERENCES
Cichosz, P. (2000). Learning Systems. WNT, Warszawa.
Doherty, P. (2005). Knowledge representation and
unmanned aerial vehicles. In Proc. of the
IEEE/WIC/ACM Int. Conf. on Web Intelligence. IEEE
Press.
Dudek-Dyduch, E. (1990). Formalization and Analysis of
Problems of Discrete Manufacturing Processes, vol-
ume 54 of Scientific bull. of AGH Academy of Science
and Tech., Automatics. AGH Academy of Science and
Tech., Cracow.
Dudek-Dyduch, E. (2000). Learning based algorithm in
scheduling. Journal of Intelligent Manufacturing,
11(2):135–143.
Dudek-Dyduch, E. and Dyduch, T. (1988). Scheduling
some class of discrete processes. In Proc. of 12th
IMACS World Congress, Paris.
Dudek-Dyduch, E. and Dyduch, T. (1992). Control of
discrete event processes - branch and bound method.
In Proc. of IFAC/Ifors/Imacs Symposium Large Scale
Systems: Theory and Applications, volume 2, pages
573–578. Chinese Association of Automation.
Dudek-Dyduch, E. and Dyduch, T. (1993). Formal ap-
proach to optimization of discrete manufacturing
processes. In Hamza, M., editor, Proc. of the Twelfth
IASTED Int. Conference Modelling, Identification and
Control. Acta Press, Zurich.
Dudek-Dyduch, E. and Fuchs-Seliger, S. (1993). Approx-
imate algorithms for some tasks in management and
economy. System, Modelling, Control, 1(7).
Kolish, R. and Drexel, A. (1995). Adaptive search for solv-
ing hard project scheduling problems. Naval Research
Logistics, 42.
Liebowitz, J. (1998). The Handbook of Applied Expert Sys-
tems. CRC Press.
McGuinness, D. and Patel-Schneider, P. (1998). Usability
issues in knowledge representation systems. In Proc.
Of XV National Conf. on Artificial Intelligence, M adi-
son, Wisconsin.
Pearl, J. (1988). Heuristics : Intelligent search strategies for
computer problem solving. Addison-Wesley Comp.,
Menlo Park.
Rajedran, C. (1994). A no wait flow shop scheduling heuris-
tic to minimize makespan. Journal of Operational Re-
search Society, 45:472–478.
Sprecher, A., Kolish, R., and Drexel, A. (1995). Semiactive,
active and not delay schedules for the resource con-
strained project scheduling problem. European Jour-
nal of Operational Research, 80:94–102.
Tadeusiewicz, R. and Dudek-Dyduch, E. (1998). Construc-
tion of branch & bound decision tree in optimiza-
tion of discrete manufacturing processes. In Dudek-
Dyduch, E., editor, Computer Science in Manage-
ment, pages 169–180. Poldex, Krakow.
Vincke, P. (1992). Multicriteria decision-aid. John Wiley
& Sons.
Zhonghao, W., Xinyu, S., Guojun, Z., and Haiping, Z.
(2005). Integration of variable precision rough set
and fuzzy clustering: An application to knowledge ac-
quisition for manufacturing process planning. Lecture
Notes in Computer Science, 3642.
ICINCO 2006 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
166
