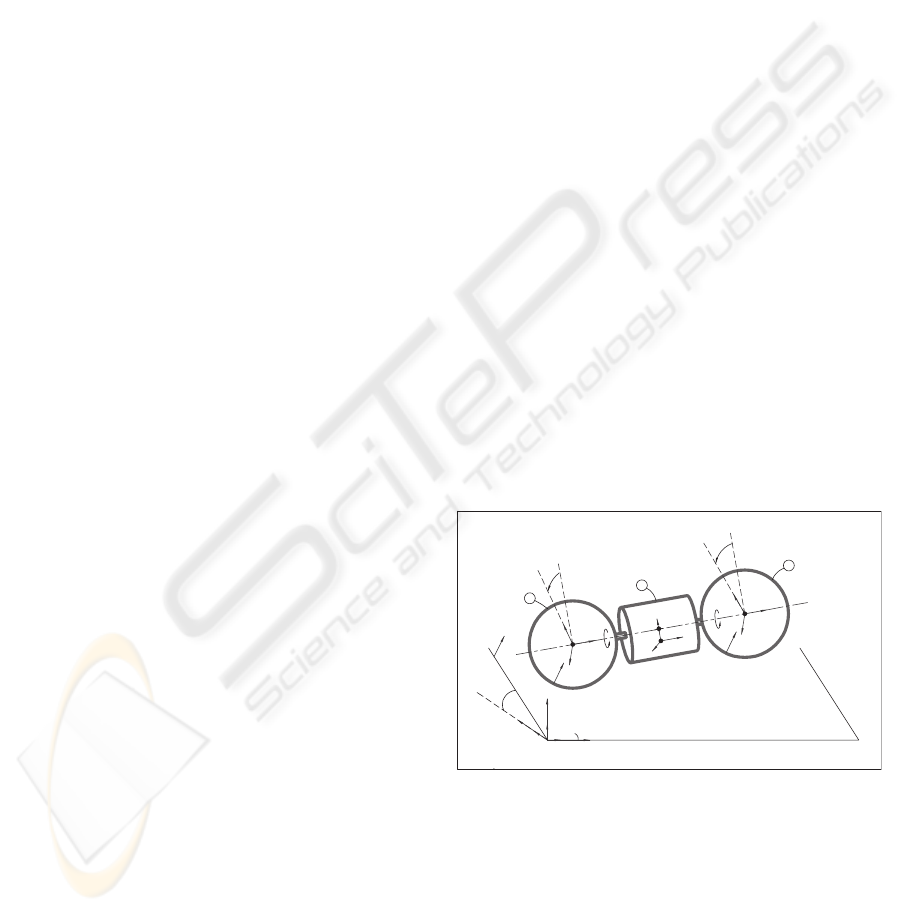
ROBUST POSTURE CONTROL OF A MOBILEWHEELED

PENDULUM MOVING ON AN INCLINED PLANE

Danielle Sami Nasrallah

1†

, Hannah Michalska

2†

and Jorge Angeles

1†

Department of Mechanical Engineering,

Department of Electrical and Computer Engineering,

and

†

Centre for Intelligent Machines

McGill University, Montreal, Canada

Keywords:

Wheeled Robots, Nonholonomy, Posture Control, Inclined Plane, Zero-Dynamics, Lyapunov Functions, Slid-

ing Mode, Invariance, Parameters Uncertainties.

Abstract:

The paper considers a speciﬁc class of wheeled mobile robots referred to as mobile wheeled pendulums

(MWP). Robots pertaining to this class are composed of two wheels rotating about a central body. The main

feature of the MWP pertains to the central body, which can rotate about the wheel axes. As such motion is

undesirable, the problem of the stabilization of the central body in MWP is crucial. The novelty of the work

presented here resides in the construction of a three-imbricated loop controller that delivers the full control

strategy for the robot posture and copes with parameters uncertainties. Simulations on the performance of the

controlled system are provided.

1 INTRODUCTION

This paper introduces a three-loop robust control

scheme for controlling the posture of an anti-tilting

outdoor mobile robot, ATOM, moving on an inclined

plane. ATOM is composed of three rigid bodies: the

central body, a cylinder whose center of mass is offset

from its geometric center, and two spherical wheels

rotating about the central body, as shown in Fig. 1.

The system inputs are the two torques applied to the

wheels. According to its structure, ATOM pertains

to the class of Mobile Wheeled Pendulums (MWP).

Many developments in the ﬁeld of MWP have been

reported recently: the US patent behind the Gin-

ger and then the Segway Human Transporter projects

(Kamen et al., 1999), JOE, a mobile inverted pendu-

lum (Grassser et al., 2002), and, more recently, Qua-

simoro, a quasiholonomic mobile robot (Salerno and

Angeles, 2004). A feature common to MWPs, that

is not encountered in other wheeled robots, is that

their central body, which constitutes the robot plat-

form, can rotate about the wheels axis. This motion

must not occur, leading to a new challenging prob-

lem for MWP which is the stabilization of the cen-

tral body, aside the classical control problem due to

nonholonomy. Therefore, although an intensive liter-

ature has dealt with the control of wheeled robots in

the past (Campion et al., 1990; Samson and Abder-

rahim, 1999; Astolﬁ, 1994; Wit and Sordalen, 1992;

Chwa, 2004; Guldner and Utkin, 1994), the control

techniques reported there cannot be applied to MWP

directly.

Figure 1: ATOM robot.

or example, any attempt to control the robot mo-

tion in conventional input-output mode results in un-

stable zero-dynamics, unless a friction torque is in-

troduced between the central body and the wheels—

such friction damps naturally the oscillation and elim-

inates trivially the serious issue of unstable zero-

dynamics as it has been the case in (Grassser et

al., 2002; Salerno and Angeles, 2004). (Pathak et

al., 2005) were the ﬁrst to attempt a solution to the

Sami Nasrallah D., Michalska H. and Angeles J. (2006).

ROBUST POSTURE CONTROL OF A MOBILEWHEELED PENDULUM MOVING ON AN INCLINED PLANE.

In Proceedings of the Third International Conference on Informatics in Control, Automation and Robotics, pages 34-41

DOI: 10.5220/0001213100340041

 SciTePress

problem of the unstable zero-dynamics. This was

done by introducing a two-layer controller. How-

ever, such stabilization of the central body is achieved

only locally, i.e., for inclination angles of the central

body near zero, as conventional linearization is em-

ployed. Moreover, the controller proposed there lacks

robustness with respect to parameters uncertainties.

Furthermore, most of the work done in the ﬁeld of

wheeled robots to date, including the references cited

above, considers robots moving on a horizontal plane.

In the light of previous contributions, the novelty of

the work reported here is as outlined below:

1. To the best of the authors’ knowledge, this is the

ﬁrst attempt to fully control the posture of a MWP-

class robot moving on an inclined plane.

2. The posture control is achieved simultaneously

with the stabilization of the central body, except

that no restrictions on the central body inclina-

tion are considered, thus rendering the control pro-

posed here global, and solving the unstable zero-

dynamics problem regardless of the central body

inclination. The control is accomplished by using

a three-loop feedback structure with (i) the inner

loop, based on input-output linearization, respon-

sible for the stabilization of the central body and

the control of the steering rate, (ii) the intermedi-

ate loop, based on an intrinsic dynamic property

that is referred to as the natural behavior of the

system, responsible for the control of the heading

velocity, and (iii) the outer loop, based on sliding-

mode control and Lyapunov functions for naviga-

tion, responsible for the posture control. It is note-

worthy that after stabilizing the central body and

controlling heading and steering velocities, the sys-

tem becomes equivalent to any car-like robot, thus

allowing the application of conventional techniques

for position and orientation control. Therefore, the

structure of the external loop is based on the work

reported in (Guldner and Utkin, 1994), with an

additional improvement to ensure smooth entering

into the sliding mode.

3. It is shown that a special choice of the general-

ized coordinates (Euler-Rodrigues parameters, as

opposed to Euler angles used in all the other ref-

erences), combined with a particular selection of

the system output functions in the inner loop, glob-

ally linearizes the dependence between the selected

output variables of the inner loop and the forward

acceleration of the robot. It is this feature that

makes the approach outlined here more powerful

than that of (Grassser et al., 2002; Salerno and An-

geles, 2004; Pathak et al., 2005), as it eliminates

the need to apply local linearization, rendering the

technique completely global and nonlinear. More-

over, this linear dependance allows us to imple-

ment a linear controller for the intermediate loop,

which, combined to the sliding-mode controller of

the outer loop, renders the full control scheme less

sensitive to parameters uncertainties.

The paper is organized in sections 2–4 below. In

Section 2 we formulate the system state-space repre-

sentation. In Section 3 we construct the three-loop

controller. In Section 4 we present the simulation re-

sults conﬁrming the expected performance of the con-

troller.

2 MATHEMATICAL MODEL

The spherical shape of ATOM’s wheels allows the ro-

bot to recover its posture after ﬂipping over, thus ren-

dering it anti-tilting. Moreover, the centers of mass of

the wheels are assumed, by design, to coincide with

the geometric centers of the spheres, while the center

of mass of the central body is offset from its geomet-

ric center. The wheels are denoted bodies 1 and 2,

while the central body is body 3, the symbols used

for the robot modeling being summarized in Table 1.

The Euler-Rodrigues parameters r

and r are used to

Table 1: List of Symbols.

b Distance between the wheel centers

Position vector of the center of mass

of the i

body, i = 1, 2, 3

Position vector of the geometric center

of the central body

d Offset between the geometric center

and the center of mass of the central

body

{i, j, k} Right-handed orthogonal triad descri-

bing the orientation of the inertial

frame F

l Unit vector along the line of wheel

centers, directed from C

to C

Mass of the central body

Mass of each wheel

n Unit vector normal to the inclined

plane

Radius of each wheel

, r Euler-Rodrigues parameters descri-

bing the orientation of the central body

, l, v

} Right-handed orthogonal triad descri-

bing the orientation of the i

body

Unit vector directed from C

to C

Inertia matrix of the central body

Inertia matrix of each wheel

Angular displacement of the i

wheel

with respect to the central body

Torque applied to the i

wheel

Angular velocity vector of the i

body in F

ROBUST POSTURE CONTROL OF A MOBILEWHEELED PENDULUM MOVING ON AN INCLINED PLANE

describe the orientation of body 3 in the inertial frame

. In our previous work (Nasrallah et al., 2005), the

mathematical model of ATOM moving on a general

warped surface was developed. The terrain geome-

try enters the dynamics explicitly via the vectors nor-

mal to the ground at the contact points. Moreover, the

particular case corresponding to the motion on an in-

clined plane is also included. Furthermore, in a more

recent work (Nasrallah et al., 2006), we performed a

model reduction that facilitates understanding the in-

trinsic dynamic properties of the system. Therefore,

we present below the state-space formulation of the

reduced model.

The six-dimensional vector of generalized coordi-

nates q is deﬁned as

q =





(1)

while the three-dimensional vector of independent

velocities is

v = [

]

(2)

where v

is the heading velocity of the robot,

namely,

(

+ 2ω

)

while ω

is the robot steering rate, given by

(

−

)

and ω

is the projection along the line of (wheels)

centers of ω

, the angular velocity of the central body.

The nine-dimensional state vector thus becomes





(3)

and the full state-space model of the system is, in

turn,

x = f (x) + g

, r)τ

+ g

, r)τ

(4)

where

f(x) =







(1/2)(r

1 − R)(ω

n + ω

−(1/2)r

(ω

n + ω







while





and g





with





+ F

+ G

)

(2r

/b)(F

+ G

)

+ G





and





−J





, g





(2r

/b)J





Moreover, h is a unit vector given by

h = l × n

while R is the cross-product matrix (CPM)

of vector r, and 1 is the 3 × 3 identity matrix.

Furthermore the input torques τ

and τ

have been

transformed into τ

and τ

, as follows

= τ

+ τ

and τ

= τ

− τ

(5)

and

, r, v) = J

[−4C

+ (2/r

]

, r, v) = (J

− J

)(b/r

(ω

+ ω

)

(b/r

, r, v) = −J

(b/r

(ω

+ ω

)

−J

(b/r

, r) = −2J

g d(r

/b)(v

× n)

, r) = (J

− J

)(2m

+ m

)g r

g d u

, r) = −J

g d u

k − J

(2m

+ m

)g r

, r) = m

/b)h

, r) = m

d/b)h

, r) = (r

/b)(I

− I

, r) = C

+ C

= 2(r

/b)

+ I

+ m

= −2(r

/b)

+ m

= I

+ m

= I

+ m

, r) = (r

/b)

[(I

+ m

+ I

]

, r) = m

d/2)h

, r) = (1/2)/(I

− I

+ 2I

)

, r) = I

/(I

− 2I

)

, r) = (I

− I

)/(I

− 2I

)

, r) = (I

/2 − I

)/(I

− 2I

)

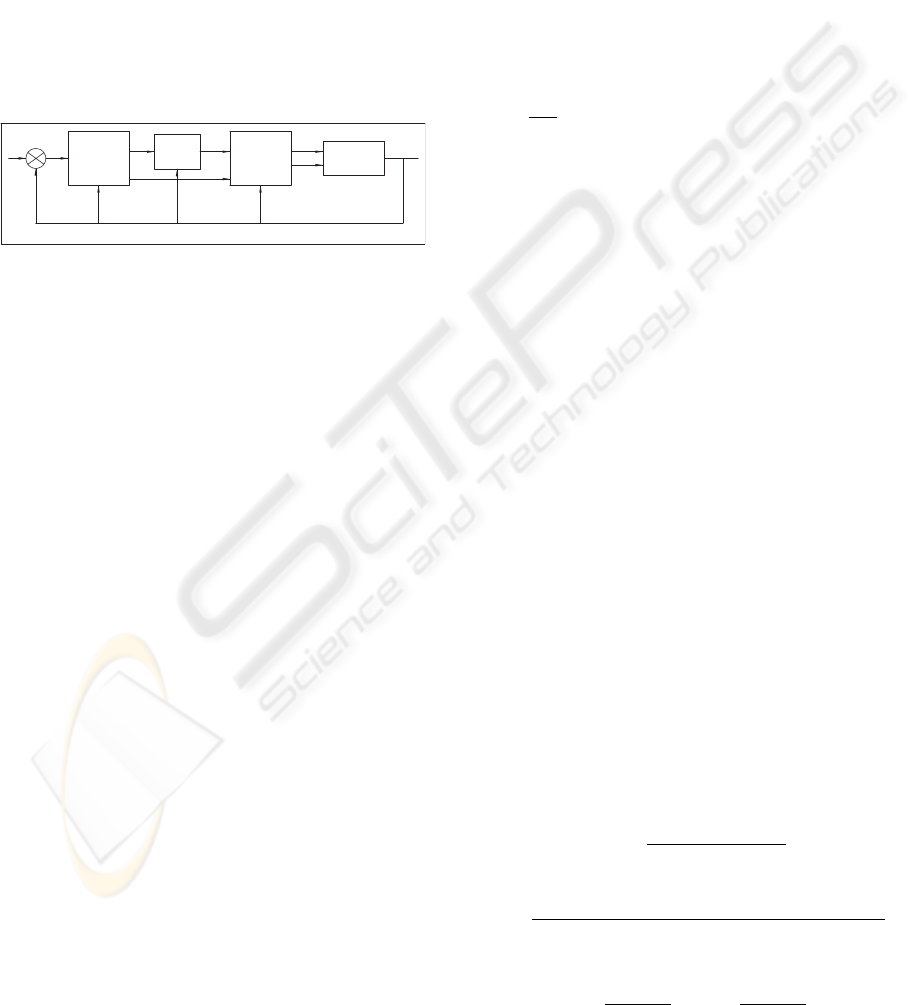
3 POSTURE CONTROL

In this section we discuss posture control of ATOM

as it moves on an inclined plane. This control objec-

tive must be achieved simultaneously with the stabi-

lization of the central body in order to avoid unstable

zero-dynamics. The controller introduced here has a

triple-loop feedback structure, as shown in Fig. 2. The

task of the inner loop is to control, via the system in-

puts τ

and τ

, two variables: (i) the steering rate

The CPM of a vector v ∈ IR

is deﬁned, for every

x ∈ IR

as well, as V = CPM(v) = ∂(v × x)/∂x

ICINCO 2006 - ROBOTICS AND AUTOMATION

, and (ii) a function of the system outputs. It is

worth noticing that this function is chosen judiciously

in order to stabilize the central body and to provide

a linear dependence with the heading acceleration ˙v

Then, the task of the intermediate loop is to control

the heading velocity v

, while the task of the outer

loop is to control the robot position and orientation

via v

and ω

using sliding mode control with Lya-

punov function for navigation. Note that the interme-

diate loop beneﬁts of an intrinsic dynamical property

that is referred to as the natural behavior of the sys-

tem and was introduced in a previous work (Nasrallah

et al., 2006). In the present work, we will employ that

property.

Position

Orientation

control

Heading

velocity

control

Central body

oscillation

Turning rate

control

ATOM

∗

Figure 2: The block diagram of the robot and its associated

control scheme.

The triple-loop controller is designed in sections 1–

6 below. In Section 1 we introduce the normal form

leading to the input-output linearization of the system.

In Section 2 we synthesize the inner-loop. In Section

3 we derive the explicit relation between the heading

acceleration and the output function of the inner loop.

In Section 4 we synthesize the intermediate loop. In

Section 5 we deﬁne the Lyapunov function for nav-

igation and the sliding surface that will be used for

posture control and synthesize the outer-loop. In Sec-

tions 6 and 7 we analyze the system stability and the

zero-dynamics.

3.1 Normal Form

The well-known notions of vector relative degree and

normal form (Sastry, 1999) are the essential tools in

input-output linearization. The normal form is dis-

played here, while omitting the intermediate calcula-

tions for the sake of brevity. These calculations are

preceded by the determination of the dimension of the

largest linearizable subsystem, following the meth-

ods suggested in (Marino, 1986). As it turns out,

the dimension of the largest linearizable subsystem

of ATOM is four (Nasrallah et al., 2006). Therefore,

the output functions of the system, whose relative de-

gree must not exceed four, are chosen so as to secure

the control over the oscillations of the central body as

well as the robot turning rate. The speciﬁc form of the

ﬁrst output function ξ

involves a thorough analysis

of the dependence of the output upon the heading ac-

celeration of the robot. Speciﬁcally, the construction

employs the additional requirement that the function

be chosen to be linear with respect to the heading

acceleration of the robot. The outputs are hence pro-

posed to be

(x) = u

(x) =

k = u

(k × n) ω

− v

k ω

(x) = ω

(6)

To complete the coordinate system, six more transfor-

mation functions η

(x) are constructed. The distrib-

ution spanned by g

and g

being involutive, those

distributions are constructed by requiring that:

∂η

∂x

(x) = 0, j = 1, 2, 1 ≤ i ≤ 6

Consequently,

(x) = x

(x) = h

(x) = y

(x) = l

(x) = v

k η

(x) = J

+ r

It is straightforward to demonstrate that

as well

as ˙η

, for i = 1, . . . , 6, do not depend on the input

torques. Indeed, τ

and τ

act directly on

and

as shown below:

(x) = d

+ (2r

/b)J

(k × n) τ

+ J

k τ

(x) = d

+ (2r

/b)J

(7)

where d

and d

represent the system drift terms,

namely,

(k × n) ω

−

k ω

− v

k (F

+ G

)

+(2r

/b)u

(k × n) (F

+ G

)

= (2r

/b)(F

+ G

)

3.2 Inner-Loop

Let ξ

∗

and ξ

∗

denote the reference values for ξ

and

, respectively. Adopting a second- and ﬁrst- order

system for the error dynamics of ξ

and ξ

, respec-

tively, yields:

+ k

(ξ

− ξ

∗

) = 0

+ k

(ξ

− ξ

∗

) = 0

which, by virtue of eq. (7), implies:

= −

+ k

(ξ

− ξ

∗

)

(2r

/b)J

(8)

and

= −

+ (2r

/b)J

(k × n)τ

+ k

(ξ

− ξ

∗

)

(9)

Consequently,

+ τ

, τ

− τ

ROBUST POSTURE CONTROL OF A MOBILEWHEELED PENDULUM MOVING ON AN INCLINED PLANE

3.3 Relation between ˙v

and u

From eq. (4) the forward acceleration ˙v

˙v

= r

+ F

+ G

) + r

When the internal loop reaches its steady-state, i.e., ξ

and ξ

reach their associated reference values, ξ

, the

ﬁrst-order time-derivatives of ξ

, vanishes; similarly,

and ω

vanish as well, thereby leading to

= 0, F

= 0

and

, τ

= −

Thus, the acceleration in the steady-state is

˙v

= r



+ G



which, after simpliﬁcation, becomes

˙v

= d

+ k

k = d

+ k

(10)

where

= −

(2m

+ m

)gr

2(I

− I

)

and

2(I

− I

)

Equation (10) shows the possibility of controlling the

heading velocity of the robot via the output func-

tion ξ

, which represents the inclination of the central

body. Moreover, the linear form of ξ

with respect to

the heading acceleration delivers global stabilization

of the central body.

3.4 Intermediate-Loop

Let v

∗

denote the reference value for the forward ve-

locity. After compensation of the drift d

, the trans-

fer function of the intermediate closed loop in the

Laplace domain becomes

(s)

∗

(s)

/s) C(s)

1 + (k

/s) C(s)

where C(s), the controller transfer function, has

the simple structure of a ﬁrst-order system, namely,

/(1 + τ

s). Thus,

∗

= −

+ L

−1

[C(s)(V

∗

(s) − V

(s))] (11)

where L

−1

denotes the inverse Laplace transforma-

tion.

Moreover, knowing that |u

k| is bounded by 1, the

value of ξ

∗

is to be restricted to [−1, 1]. However,

since v

k vanishes at the boundaries, this interval is

further restricted to [-0.99,0.99].

3.5 Outer-Loop

Once the inner and intermediate loops are imple-

mented, the system (ATOM + two internal control

loops) is equivalent to any car-like robot, since the

platform is stabilized and the new control inputs are

and ω

, the heading and steering velocities, re-

spectively. For the construction of the position and

orientation controller, the technique introduced in

(Guldner and Utkin, 1994) is applied. It is based on

sliding-mode control with Lyapunov function, as ap-

plied to a navigation problem and is additionally en-

hanced by a feature allowing smooth entry into the

sliding mode. The central idea is to ensure that vec-

tor h is linearly dependent with a vector ǫ, which is

deﬁned as the gradient of the chosen Lyapunov func-

tion. When linear dependency is achieved, the sys-

tem enters the sliding mode. The foregoing linear de-

pendence condition does not require any switching,

which guarantees that the distance between the cur-

rent position of the system and the sliding surface de-

creases monotonically.

Finally, without loss of generality, the origin of the

workspace is located at the goal posture and oriented

in such a way that the line of wheel centers is paral-

lel to the one of steepest ascent and the line joining

the center of mass of the central body to its geometric

center is normal to the plane. Therefore the reference

values for the posture controller are:

= 0, y

= 0 and |u

k| = 1

Let s be the direction of steepest ascent of the inclined

plane, i.e.,

s = n × i

Then the x and y coordinates of

can be written as

˙x

= v

i and ˙y

= v

cos β h

where β represents the inclination of the plane.

The Lyapunov function V for the navigation problem

is chosen as

V (x

, y

) =



+ y



so that ǫ is deﬁned by

ǫ(x

, y

) = −grad (V ) =







−x

−y



Therefore, the equation of the sliding surface be-

comes

∆(q) = det



i ǫ

/kǫk

s ǫ

/kǫk



= 0 (12)

where kǫk denotes the Euclidian norm of ǫ.

Differentiating ∆ with respect to time leads to

∆ = −D

(q) ω

+ D

(q) v

ICINCO 2006 - ROBOTICS AND AUTOMATION

where

(q) = h

kǫk

+ h

kǫk

and

(q) =

4kǫk



− 2 cos βh



i h

4kǫk



−cos βx

+ 2y



Convergence of ∆ to zero within ﬁnite time can be

achieved by imposing

∆ = −ζ

|∆|sign(∆) with ζ ≥ 0

leading to

∗

= ω

∗



+ ζ

|∆|sgn(∆)



(13)

Finally, introducing a positive scalar v

as an auxiliary

control input yields

∗

= kǫkv

sgn(h

i ǫ

) (14)

Therefore, eqs. (8), (9), (11), (13), and (14) consti-

tute the controller as implemented in three loops.

3.6 Analysis of the Stability

Equation (12) implies h

i = ±ǫ

/kǫk. Considering

the positive case

˙x

= v

i = v

/kǫk = v

kǫk

˙y

= v

cos β h

i = v

cos β ǫ

/kǫk = v

cos β ǫ

Thus,

V = −ǫ



˙x

˙y



= −ǫ

− ǫ

cos β v

≤ 0

The same reasoning is employed for the negative case,

thus ensuring system stabilization by standard Lya-

punov asymptotic stability theory.

3.7 Analysis of the Zero-Dynamics

The zero-dynamics of the system is calculated by de-

termining initial conditions and inputs such that the

output of the system remains zero for all the time

(Nasrallah et al., 2005). If the initial posture with the

state x

is such that the line of wheel centers is par-

allel to the direction of steepest ascent, and the line

joining the center of mass of the central body to its

geometric center is perpendicular to the plane, then it

is a simple matter to verify that the zero dynamics is

described by

˙η

= v

and ˙η

= 0 for i = 2 . . . 6

Here, v

, the initial heading velocity, decreases to

zero because of the action of the outer-loop controller,

which secures stable zero-dynamics.

4 SIMULATION RESULTS

In this section we present the simulation results for the

closed-loop system. The inclination of the plane is of

30% for all the simulations. ATOM succeeds to reach

the origin at the desired orientation starting from dis-

tinct initial conditions. Below we display four exam-

ples:

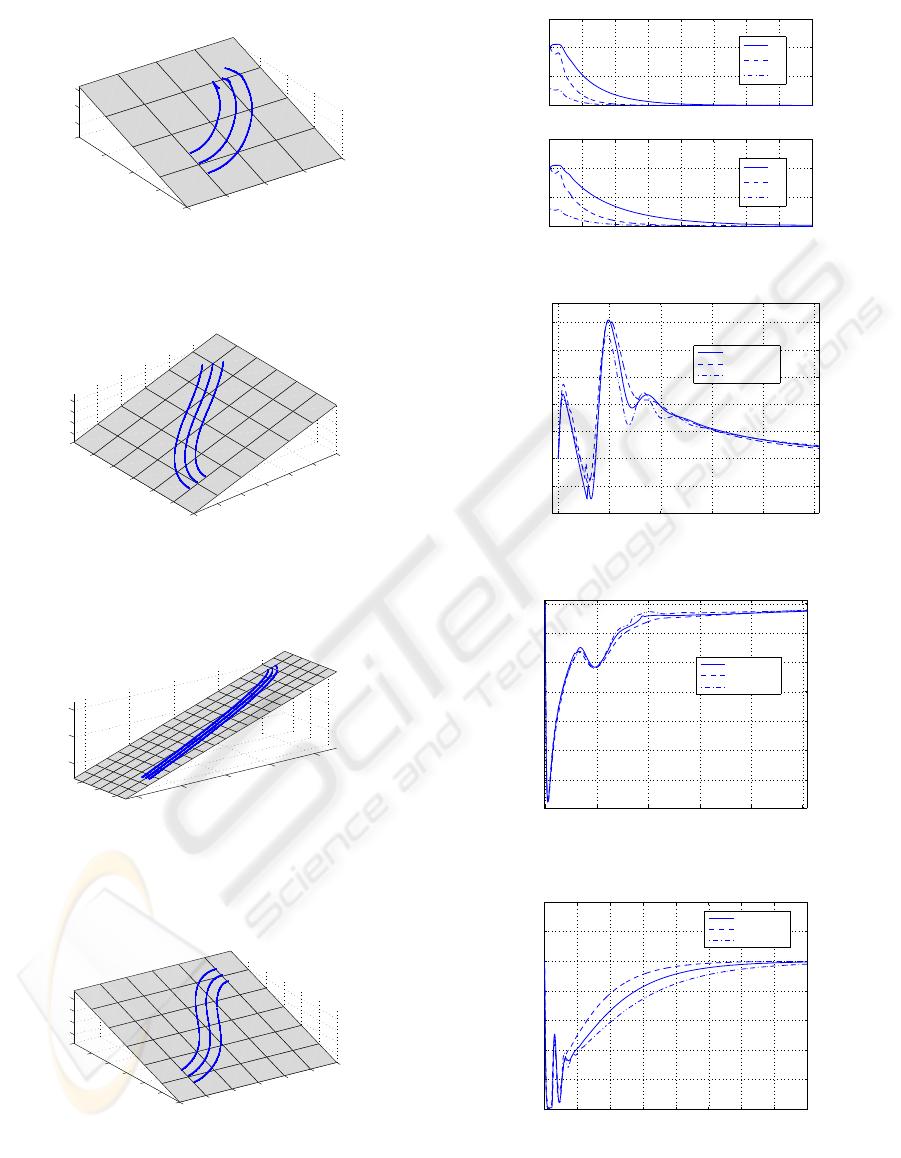
1. coming from up right, Fig. 4(a)

= 1 , y

= 1 and u

i = −

√

2/2

2. coming from up left, Fig. 4(b)

= −2 , y

= 2 and u

i = −

√

2/2

3. coming from down right, Fig. 4(c)

= 2 , y

= −7 and u

i = 0

4. coming from down left, Fig. 4(d)

= 1 , y

= 1 and u

i = −

√

2/2

Furthermore, we test the controller performance

versus the parameter uncertainties. We recall here

that the controller is composed of three-imbricated

loops. The inner loop, based on input-output lin-

earization, is obviously dependent of the robot para-

meters. As for the intermediate loop, the judicious

choice of the function ξ

allowed a linear dependence

between the heading acceleration of the robot and this

function. Therefore, we were able to implement a lin-

ear controller C(s), with constant parameters. For

the outer loop the choice of the sliding-mode control

and the auxiliary constant input v

rendered the con-

troller less dependent of the system parameters. Note

that the choice of the controller parameters was not

a simple task since the system itself is nonsymmet-

ric, due to the up and down motion of ATOM on the

inclined plane. Therefore, we show two simulations

of ATOM moving on the same inclined plane with a

slope of 30%, except that the robot and terrain pa-

rameters seen by the controller are over- and under-

estimated, respectively. The error on the normal vec-

tor to the ground is of 10%, while the error on the

moments of inertia of the rigid bodies composing the

robot and the offset d between the geometric and cen-

ter of mass are of 20%. In both cases, i.e., under- and

over-estimation, ATOM succeeds to reach the origin

with the desired orientation, which can be veriﬁed by

looking to the evolution in time of the x−, y−, and

z− components of C

depicted in Fig. 4(a). The time

history of the signals v

, ω

, and ξ

are displayed in

Fig. 4(b), (c), and (d), respectively. The torques ap-

plied to the wheels in Fig.5.

ROBUST POSTURE CONTROL OF A MOBILEWHEELED PENDULUM MOVING ON AN INCLINED PLANE

−0.5

0.5

1.5

−0.5

0.5

1.5

0.2

0.4

x (m)

y (m)

z (m)

(a)

−2.5

−2

−1.5

−1

−0.5

0.5

−0.5

0.5

1.5

2.5

0.2

0.4

0.6

y (m)

x (m)

z (m)

(b)

−8

−6

−4

−2

0−2

−1

y (m)

x (m)

z (m)

(c)

−2.5

−2

−1.5

−1

−0.5

0.5

−2.5

−2

−1.5

−1

−0.5

0.5

−0.6

−0.4

−0.2

x (m)

y (m)

z (m)

(d)

Figure 3: Manoeuvres performed by ATOM on the inclined

plane: reaching the origin at the desired orientation from (a)

up right; (b) up left; (c) down right; and (d) down left.

0 5 10 15 20 25 30 35 40

0.5

1.5

over estimation

0 5 10 15 20 25 30 35 40

0.5

1.5

Time (s)

under estimation

(a)

0 2 4 6 8 10

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

Time (s)

(m/s)

exact param.

over estimat.

under estimat.

(b)

0 2 4 6 8 10

−1.2

−1

−0.8

−0.6

−0.4

−0.2

Time (s)

(rd/s)

exact param.

over estimat.

under estimat.

(c)

0 5 10 15 20 25 30 35 40

−1

−0.8

−0.6

−0.4

−0.2

0.2

0.4

Time (s)

exact param.

over estimat.

under estimat.

(d)

Figure 4: Controller performance versus parameters uncer-

tainties: time-history of: (a) the x−, y−, and z− compo-

nents of C

; (b) v

; (c) ω

; and (d) ξ

ICINCO 2006 - ROBOTICS AND AUTOMATION

0 5 10 15 20 25 30 35 40

−3

−2

−1

(N.m)

0 5 10 15 20 25 30 35 40

−1.5

−1

−0.5

0.5

(N.m)

Time (s)

exact param.

over estimat.

under estimat.

exact param.

over estimat.

under estimat.

(a)

Figure 5: Controller performance versus parameters uncer-

tainties: time history of τ

and τ

5 CONCLUSION

The work reported here delivers a robust posture con-

troller for a MWP-class robot moving on an inclined

plane. The challenging issue in this design is to be

able to control the posture of the robot simultaneously

while stabilizing of the central body, which results in

the absence of friction. Unlike previous attempts to

control such systems, our controller is global and less

sensitive to errors in the parameters estimation. We

show that deep insight into the internal dynamics of

the system, in conjunction with proper selection of

a coordinate system and the system output function,

are instrumental in the construction of feedback con-

trollers for nonholonomic systems underlying unsta-

ble zero-dynamics.

Future work will focus on generalization of the mo-

tion of the robot to a warped, smooth surface.

ACKNOWLEDGEMENTS

This work was made possible by NSERC (Canada’s

Natural Sciences and Engineering Research Council)

Grant OGP4532.

REFERENCES

D. L. Kamen, R. R. Ambrogi, R. J. Duggan, R. K. Heinz-

mann, B. R. Key, A. Skoskiewicz, P. K. Kristal, 1999,

“Transportation Vehicles and Methods”, US patent

5,971,091.

F. Grassser, A. D’Arrigo, S. Colombi and A. C. Rufer, 2002,

“JOE: A Mobile, Inverted Pendulum”, IEEE Trans.

Industrial Electronics 49, No. 1, pp. 107-114.

A. Salerno and J. Angeles, 2004, “The Control of Semi-

Autonomous Self-Balancing Two-Wheeled Quasi-

holonomic Mobile Robots”, Proc. 15th CISM-

IFToMM Symposium on Robot Design, Dynamics and

Control (RoManSy), Montreal, June 14-18.

G. Campion, B. d’Andrea-Novel and G. Bastin, 1990,

“Controllability and State Feedback Stabilizability of

Non Holonomic Mechanical Systems”, Advanced Ro-

bot Control, Proc. of the International Workshop on

Nonlinear and Adaptive and Control, Issues in Robot-

ics, Grenoble, November 21-23

C. Samson, K. Ait-Abderrahim, 1999, “Mobile Robot Con-

trol Part 1: Feedback Control of a Nonholonomic

Wheeled Cart in Cartesian Space”, INRIA, Rapport

de Recherche, No.1288, October.

A. Astolﬁ, 1994, “On the Stabilization of Nonholo-

nomic Systems”, Proc. 33rd Conference on Decision

and Control, Lake Buena Vista, December 14-16,

pp. 3481-3486.

C. Canudas de Wit, O. J. Sordalen, 1992, “Exponential Sta-

bilization of Mobile Robots with Nonholonomic Con-

straints”, IEEE Trans. Automatic Control 37, No. 11,

pp. 1791-1797.

D. Chwa, 2004, “Sliding-Mode Tracking Control of Non-

holonomic Wheeled Mobile Robots in Polar Coordi-

nates”, IEEE Trans. Control Systems Technology 12,

No. 4, pp. 637-644.

J. Guldner, V. I. Utkin, 1994, “Stabilization of Nonholo-

nomic Mobile Robots Using Lyapunov Functions for

Navigation and Sliding Mode Control”, Proc. 33rd

Conference on Decision and Control, Lake Buena

Vista, December 14-16, pp. 2967-2972.

K. Pathak, J. Franch and S. K. Agrawal, 2005, “Velocity

and Position Control of a Wheeled Inverted Pendulum

by Partial Feedback Linearization”, IEEE Trans. Ro-

botics 21, No. 3, pp. 505-513.

D. S. Nasrallah, J. Angeles and H. Michalska, 2005,

“Modeling of an Anti-Tilting Outdoor Mobile Robot”,

ASME Proc. 5th International Conference on Mut-

libody Systems, Nonlinear Dynamics, and Control,

Long Beach, September 25-28.

D. S. Nasrallah, J. Angeles and H. Michalska, 2006, “Veloc-

ity and Orientation Control of an Anti-Tilting Mobile

Robot Moving on an Inclined Plane”, IEEE Proc. In-

ternational Conference on Robotics and Automation,

Orlando, May 15-19, pp. 3717-3723.

S. Sastry, 1999, Nonlinear Systems: Analysis, Stability, and

Control, Springer-Verlag.

R. Marino, 1986, “On the largest feedback linearizable sub-

system”, Systems and Control Letters 6, pp. 345–351.

D.S. Nasrallah, J. Angeles and H. Michaslka, 2006, “The

Largest Feedback-Linearizable Subsystem of a Class

of Wheeled Robots Moving on an Inclined Plane”,

to appear in Proc. 16th CISM-IFToMM Symposium

on Robot Design, Dynamics and Control (RoManSy),

Warsaw, June 20-24.

ROBUST POSTURE CONTROL OF A MOBILEWHEELED PENDULUM MOVING ON AN INCLINED PLANE