
Bagging KNN Classifiers using Different Expert Fusion
Strategies
Amer. J. AlBaghdadi and Fuad M. Alkoot
Telecommunication and Navigation Institute
P.O.Box 6866, Hawally,32043, Kuwait
Abstract. An experimental evaluation of Bagging K-nearest neighbor classifiers
(KNN) is performed. The goal is to investigate whether varying soft methods of
aggregation would yield better results than Sum and Vote. We evaluate the per-
formance of Sum, Product, MProduct, Minimum, Maximum, Median and Vote
under varying parameters. The results over different training set sizes show minor
improvement due to combining using Sum and MProduct. At very small sample
size no improvement is achieved from bagging KNN classifiers. While Minimum
and Maximum do not improve at almost any training set size, Vote and Median
showed an improvement when larger training set sizes were tested. Reducing the
number of features at large training set size improved the performance of the
leading fusion strategies.
1 Introduction
Bagging Predictors [4], proposed by Breiman is a method of generating multiple ver-
sions of a predictor or classifier, via bootstraping and then using those to get an aggre-
gated classifier. Methods of combining suggested by Breiman are Voting when classifier
outputs are labels, and Averaging when classifier outputs are numerical measurements.
The multiple versions of classifiers are formed by making bootstrap [8] replicas of the
training set, and these are then used to train additional experts. He postulates the nec-
essary condition for bagging to improve accuracy as a perturbation of the learning set
causes significant changes in the classifier, namely the classifier must be unstable. Bag-
ging has been successfully applied to practical cases to improve the performance of
unstable classifiers. A sample of such papers includes [6]. Many have investigated its
performance and compared it to boosting or other methods [9, 12,7,2,13, 5]
Breimans results [4] show that bagging more than 25 replicas does not further im-
prove the performance. He also notes that a fewer replicas are required when the classi-
fier outputs are numerical results rather than labels, but more are required as the number
of classes increases. Regarding the bootstrap training set size, he used the size equal to
the cardinality of the original training set and his tests showed no improvement when
the boot training set was double the size of the original training set.
In this paper we Bagg K-NN classifiers, in order to find whether it is possible to
achieve an improvement under varying parameters. We focus on the small training set
case in which the KNN classifier can be expected to be unstable. We aggregate the
generated bootstrap sets using six different methods, namely: Sum, Product, MProduct,
J. AlBaghdadi A. and M. Alkoot F. (2005).
Bagging KNN Classifiers using Different Expert Fusion Strategies.
In Proceedings of the 5th International Workshop on Pattern Recognition in Information Systems, pages 219-224
DOI: 10.5220/0002572002190224
Copyright
c
SciTePress

Minimum, Maximum, Median and Vote. MProduct is a method proposed by [1] which
improves Product under small sample size situations where the veto effect exists. The
rest of the rules are commonly used [11, 10]. We repeat the experiments under varying
feature set sizes and training set sizes. In our experiments one synthetic, two class, sym-
metric data set, was used, in addition to nine real data sets which were obtained from the
UCI- Repository, via the web [3]. We follow Breimans guidelines in our experiments
and limit the bagging to 25 bootstrap sets using a training set size equal to the size of
the original training set. K is selected to be the square root of the number of training
samples N in a bootstrap or learning set,i.e. K =
√
N . We evaluate the performance of
the adopted fusion strategies under varying parameters. The results over varying train-
ing set sizes show minor improvement due to bagging in conjunction with the Sum and
MProduct combination rules. At very small sample size, no improvement is achieved
from bagging KNN classifiers. While Minimum and Maximum do not improve for al-
most any training set size, Vote and Median show an improvement when larger training
set sizes were tested.
This paper is organized as follows; In section 2 the experiment methodology, data
types used and the method of calculating expert error rates are explained. Experimental
results are presented in section 3. Discussion of the obtained results and the conclusion
are noted in sections 4 and 5, respectively.
2 Experiments
2.1 The Synthetic Data Set
Controlled experiments were carried out using the computer generated data set involv-
ing two features and two classes. The two class densities have an overlap area which
was designed to achieve the maximum instability of the class boundary. The theoretical
Bayes error of this data set is 6.67%. Using the generated samples the empirical Bayes
error was found to be 6.82.
2.2 Methodology
A single training set is taken from the original sample space, The K-NN classifier built
using this original learning set is referred to as the single expert. From the remaining
samples 600 randomly selected samples were used as a test set. Using the learning set,
25 boot sets are generated, by sampling randomly with replacement, i.e. by bootstrap-
ping. The decision of the 25 boot sets are aggregated to classify a test set. These results
are referred to as the bagged expert results. We wish to compare these results to those
obtained from the single expert.
The above is repeated for varying training set sizes. When applied to real world
data, relatively similar percentages of samples from the original data set were used for
the learning set. In Contrast to the synthetic data experiment, all the remaining samples
were used as the test set.
220
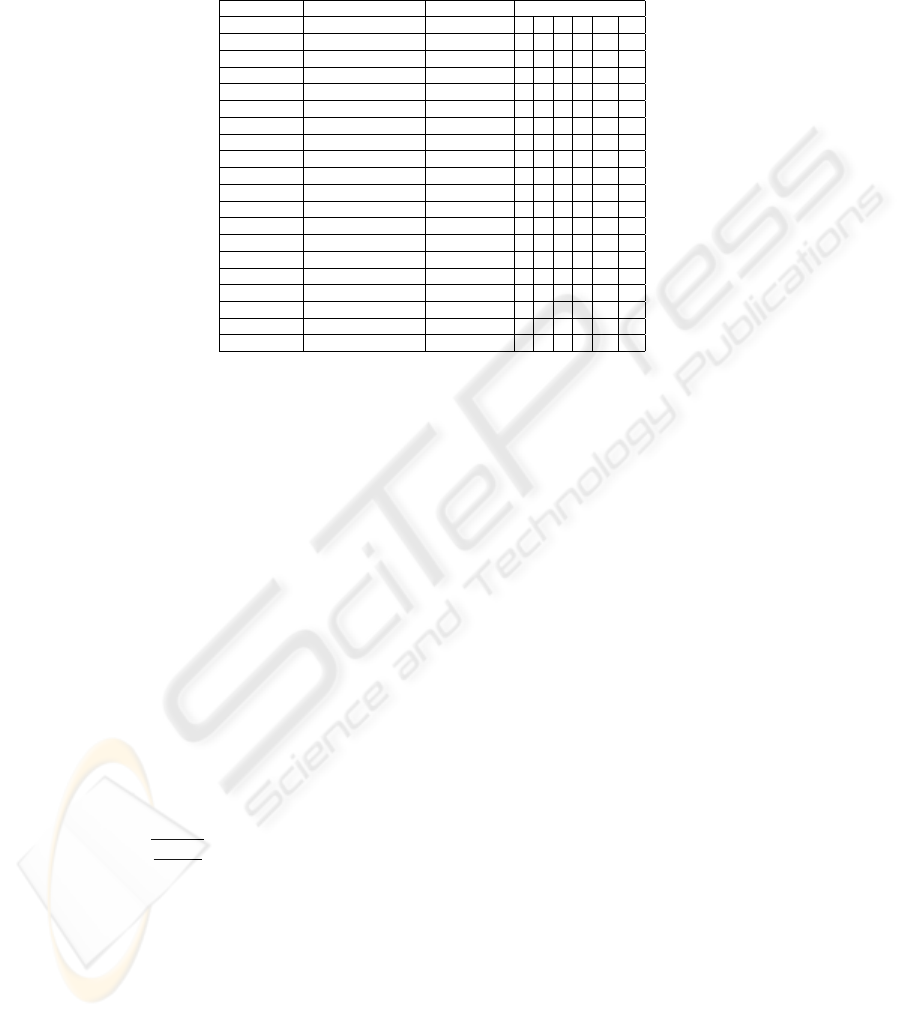
Table 1. Data sets and the number of training samples used for each data set. Under the training
set size columns, the first row indicates the number of samples, while the second row indicates
the training size in percentage.
Data Name Total No. of samples No. of features Training set size
Synthetic 1231 2 12 25 49 86 123 616
1 2 4 7 10 50
Diabet 768 8 8 15 31 54 77 614
1 2 4 7 10 80
Breast cancer 699 9 7 14 28 49 70 559
1 2 4 7 10 80
Ionosphere 351 34 4 7 14 25 35 281
1 2 4 7 10 80
Liver disorder 345 6 3 7 14 24 35 276
1 2 4 7 10 80
Ecoli 336 7 3 7 13 24 34 269
1 2 4 7 10 80
Wine 178 13 4 7 12 18 89 142
2 4 7 10 50 80
Iris 150 4 6 11 15 45 75 120
4 7 10 30 50 80
Lung Cancer 32 56 3 6 10 16 26 -
10 20 30 50 80 -
Lens 24 4 2 7 12 19 - -
10 30 50 80 - -
3 Results
3.1 Using Synthetic data
The results for the best combiner, i.e. MProduct, are summarized in table 2. The results
indicate that Maximum and Minimum have the highest error rates, and were never better
than the single expert. Only for a very small sample size of 12 samples, did the single
expert outperform all combiners. In all other sizes Sum and MProduct were the best
rules, followed by Median and Vote, which were identical. Product was the most sen-
sitive to the training set size. At low set sizes it performed as bad as Minimum, while
at large training set sizes, it performed close to Sum and MProduct. At medium size
ranges it was much better than Minimum but not always better than the single expert.
This behavior of Product was consistent for all data sets used. For all set sizes we notice
that Median and Vote have identical performance and mostly lag behind Sum, but are
very close. Maximum and Minimum give relatively close results. As we decrease the
learning set size the error rate of all rules increased. However, bagging did improve the
KNN performance at larger training set sizes, although the amount of improvement de-
creased as the set size increased. An improvement is considered significant if it is larger
than:
q
e(1−e)
N
, where N is the number of test samples used.
3.2 Using Real data
The above tests were repeated using real data obtained from the UCI repository, [3].
The performance of the rules when using the diabetic, liver, lens, ecoli, wine and iris
data is similar to when using the synthetic data. For brease cancer Sum and Mproduct
221

Table 2. Difference between single expert error rate and combiner error rate decreases as the
training set size increases for the synthetic data experiment
Training set size 12 25 49 86 123 616
Improvement in percent over single KNN -0.2598 0.0624 0.0277 0.047 0.0187 0.0112
Significance 0.0174 0.0137 0.0125 0.012 0.0114 0.0108
had an error rate lower than the KNN single expert, by .02, but only for training set
sizes above 10%. Otherwise, the single expert outperformed all aggregation methods.
For the Ionosphere data they showed a very variable performance from one training
size to another. MProduct and Sum were best at three sizes. Vote at one, Minimum and
Maximum at one and the single expert at the largest training set size. The lung cancer
was a very difficult data, with small number of samples and a very large dimension of
56 features. At small sizes MProduct and Sum were better than the single expert, but at
larger sizes the single expert was better.
3.3 Reduced features
When we randomly reduced the number of features used for each of the real data sets,
we did not notice any change in the relative performance of the rules. An exception was
observed for the training set size of 80%. In this case the relative performance changes
as the number of features used is reduced.
We repeated the experiments for a reduced number of features, equaling to half the
total number of features available, and finally reduced to 2 features. Contrary to our
expectation reducing the number of features did not always increase the error rates. For
the BCW and Iris data sets we observed the error rate to increase as the number of
features is decreased. On the other hand for the diabetic data we observed the error rate
to decrease as the number of features is reduced to 4. When it was reduced to 2 we
still had an improvement over the full feature set experiment, but not over the 4 feature
experiments. Although the relative performance did not change when four features were
used at a training set size of 80%, the Sum and MProduct were no longer better than the
single expert. They exhibited error .01% higher. These discrepancies point to the need
of more investigation in this regard.
4 Discussion
The aggregation method which was the most sensitive to the training set size was Prod-
uct. It improves at larger set sizes, and sometimes reaches the best performance pos-
sible, while at small set sizes it performed worse than all the other rules in line with
Minimum and Maximum.
The results over the varying training set sizes show minor improvement due to bag-
ging and combining using Sum and MProduct. While Minimum and Maximum do not
improve at almost any training set size, Vote and Median, in general, show an improve-
ment for larger set sizes. Vote was the best for three data sets when a very small training
set size was tested.
222

Between the six aggregation methods MProduct had the best overall performance
followed very closely by Sum. Vote had very bad performance at many phases of the
experiment. This suggests that one should be using an aggregation method other than
Voting if level III information is available. Classifiers producing level III outputs are
ones that output measurement values in addition to the ranked labels.
Table 3. The best performance rule as a function of training set size. Initial letters have been
used to indicate each rule. SE:single expert, S:Sum, M:MProduct, P:Product, MX:Maximum,
MN:Minimum, V:Vote, MD:Median
Data name Training set size
1 2 3 4 5 6
Artificial data SE M & S M & S M & S M & S M & S
Pima Indian Diabetes SE M & S M & S M & S M & S M, P & S
Wisc. Breast Cancer SE SE SE SE M & S M & P
Ionosphere V M & S M & S M & S MN SE
Liver Disorder M & S M & S M & S M & S M & S M & P
Ecoli V M, S & SE M, S & SE M, S & SE M, S P
Wine M & S SE SE M & S M & S M, P & S
Iris V SE M & S M M M, P & S
Lung cancer SE M & S M & S SE SE -
Contact lenses SE M & S M M, S & SE - -
We also notice that Vote performed best three times when data was very noisy, i.e.
for very low training set size (size 1). Also, for the same data set Sum and MProduct
were the best rules at the very low training size. In general Bagging did not work for
very small training set size (size 1). At this size, the single expert was the best for six
out of ten data sets.
5 Conclusion
It is possible to improve the performance of the KNN classifiers, especially if MProduct
or Sum are used as an aggregation method.
It was noticed that for very small sample sizes bagging may degrade the perfor-
mance as compared to the single expert. At very small sample sizes the single expert
outperforms the bagged experts because the bootstrap sets often contain samples from
one class only. In such situations the resulting very high error rates dominate the boot-
strap expert outputs and the underlying benefits of bagging are canceled. In order to
benefit from bagging, the investigation should be directed towards methods of selecting
best bootstrapped classifiers and ignoring the worst ones.
References
1. F. M. Alkoot and J. Kittler. Improving the performance of the product fusion strategy. In
Proceedings of the ICPR 2000 conference, Barcelona, Spain, 9 2000.
223

2. E. Bauer and R. Kohavi. An empirical comparison of voting classification algorithms: Bag-
ging, boosting and varients. Machine Learning, pages 1–38, 1998.
3. C.L. Blake and C.J. Merz. UCI repository of machine learning databases, 1998.
4. L. Breiman. Bagging predictors. Machine Learning, 24:123–140, 1996.
5. L. Breiman. Bias, variance and arcing classifiers. Technical Report 460, Statistics Depart-
ment, University of California at Berkeley, 4 1996.
6. P. deChazal and B. Celler. Improving ecg diagnostic classification by combining multiple
neural networks. In Computers in Cardiology, volume 24, pages 473–476. IEEE, 9 1997.
7. T. Dietterich. An experimental comparison of three methods for constructing ensembles of
decision trees: Bagging, boosting, and randomization. Machine Learning, pages 1–22, 1998.
8. B. Efron and R. Tibshirani. An Introduction to the Bootstrap. Chapman and Hall, 1993.
9. T. Heskes. Balancing between bagging and bumping. In M. Mozer, M. Jordan, and
T. Petsche, editors, Advances in Neural Information Processing Systems 9, pages 466–472.
MIT press, 1997.
10. J. Kittler. Combining classifiers: A theoretical framework. Pattern Analysis and Applica-
tions, 1:18–27, 1998.
11. J. Kittler, M. Hatef, R. Duin, and J. Matas. On combining classifiers. IEEE Trans Pattern
Analysis and Machine Intelligence, 20(3):226–239, 1998.
12. D.W. Opitz and R. F. Maclin. An empirical evaluation of bagging and boosting for artifi-
cial neural networks. In IEEE International Conference on Neural Networks - Conference
Proceedings, volume 3, pages 1401–1405, Univ of Montana, Missoula, MT, USA, 6 1997.
IEEE.
13. J. Quinlan. Bagging, boosting and c4.5. In Proceedings of the 13th National Conference on
Artificial Intelligence, volume 1, pages 725–730, Portland, OR, USA,, 8 1996. AAAI, Menlo
Park, CA, USA.
224
