A TREE BASED ALGEBRA FRAMEWORK FOR XML DATA

SYSTEMS

Ali El bekai, Nick Rossiter

School of Informatics, Northumbria University

Keywords: XML documents, tr

ee algebra, integration framework

Abstract: This paper introduces a framework in algebra for processing XML data. We develop a simple algebra,

called TA (Tree Algebra), for processing storing and manipulating XML data, modelled as trees. We

present assumptions of the framework, describe the input and the output of the algebraic operators, and

define the syntax of these operators and their semantics in terms of algorithms. Furthermore we define the

relational operators and their semantics in terms of algorithms. Examples show that this framework is

flexible to capture queries expressed in the domain specific XML query language. As can be seen the input

and output of our algebra is a tree that is the input and output are XML document and the XML documents

are defined as trees. We also present algorithms for many of the algebra operators; these algorithms show

how the algebra operators such as join, union, complement, project, select, expose and vertex work on nodes

of the XML tree or element and attributes of an XML document. Detailed examples are given.

1 INTRODUCTION

In this paper we develop an algebraic model for data

management, which unifies in a single framework

data presentation, data communications and data

processing based on an XML Schema (Zisman

2000). Starting with the XML Schema of the data

we develop domain specific XML algebra suitable

for data processing of the specific data. The

algebraic model we are developing, based on the

existing standard (W3C XML Query Algebra), is a

domain specific model of collaborative information

processing over the Web. Even though it is domain

specific, however, it will be generic since it will

model an integrated architecture for distributed

information processing. The input and output of our

algebra are XML documents defined as a tree. We

also present examples and algorithms for most

algebra operator; these examples and algorithms

show how the relational algebra and its operators

work. Furthermore we apply join, union,

complement, project, select, expose and vertex

operations to nodes to form the XML tree as

elements and attributes of XML (Bourret 2004).

The rest of the paper is structured as follows:

Sectio

n 2 presents the related work for XML

algebra. This leads up to our algebra description in

Section 3. Section 4 presents our XML data model.

Section 5 presents the algebra relational. The

examples for algorithms and input and output of the

algebra operators are defined in Section 6. Section 7

presents a discussion of the algebra.

2 RELATED WORK

Table 1 provides a summary and review of algebraic

methods discussed in this paper. It can be seen

that all have some significant drawbacks, in

particular in complexity and generality. In the next

section

we attempt to address these problems by

developing a tree-based algebra, which is more

ersatile in its application. The algebraic models we

have reviewed are IBM (Beech, M. & Rys 1999),

Lore (McHugh et al 1997), YATL (Christophides,

Cluet & Simeon 2000), Niagara algebra (Galanis et

al 2001) and AT&T a (W3C February 2001).

305

El bekai A. and Rossiter N. (2005).

A TREE BASED ALGEBRA FRAMEWORK FOR XML DATA SYSTEMS.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 305-312

DOI: 10.5220/0002528403050312

 SciTePress

Table 1: Comparison of Different Algebraic Models

Algebraic

Model

IBM

YATL

Niagara

Lore

AT&T

Data

Model

Standalone XML

algebra

Logical Data Model,

Graph Based

Standalone XML

algebra

Integrated DBMS

Standalone XML

algebra

Approach

Represents the

collection of

vertices

Integrates data from

different sources

Operates on a set of

bags of vertices

Cost-based query

optimization

Based on the

iteration operation,

NRA

Distinctive

Features

- Not system

specific,

XQuery support.

- Provides an

algebra operator

that operates as

graph-based data

model.

- Ability to integrate

data from different

sources; can be used

efficiently in querying

distributed data.

- YTAL has Tree

operations for

transforming relation

structure to Tree

structure (Codd 1972)

- Simple and powerful

algebraic expressions,

optimised rules

- Optimised from

cost-based

perspective, dynamic

schema structure.

- Each query is

transformed into a

logical query plan

using logical

operators such as

Select, Project,

Discover…etc

- Built in types for

detecting errors at

query compile

time.

- SQL& OQL and

NRA support

XQuery.

- Based on the

iteration operation

Drawbacks

- Deficiency of

Optimisation

Rules,

- Complex query

structure, data type

should be known

at query compile

time

- The integration is

exclusively based on

YATL data model and

type system, and does

not provide a well-

defined list of the

operators and explicit

optimisations.

- The algebraic

framework assumes that

at the time of writing

the query, the type is

known for each vertex

(attribute, element)

[Fenkhauser, S. 2001]

- Implementing a query

using IBM model will

lead to a complex

structure.

- The physical

operators are

designed specifically

for its own data

model

- Query plan based

on this algebra,

once generated, is

difficult to

optimize

Special

Operators

Reshaping

Operators

Bind, Tree operators - Vindex, Lindex, once -

W3C

Proposed - Proposed - Proposed

3 DESCRIPTION OF OUR

ALGEBRA

Our XML Algebra is a tree structure that consists of

algebra operators (Greenwald et al 2003). Each node

in the tree has only one parent node, but a parent

node can have multiple children nodes. The XML

Tree is interpreted top-down, so the root of the tree

at the top of the XML Tree is where the final XML

document output is produced. The leaves of the tree

correspond to the different data sources accessed,

which in our system prototype are assumed to be

object-relational (Galanis et. al 2001, Scholl 1986).

There are two types of operators in our algebra:

firstly, the algebraic operators are join, union,

complement, project, select, expose and vertex.

Every operator has a unique output of a tree,

which makes it distinct from other algebra operators.

Secondly, the relational operators are universal,

subsuming, equivalence and similarity.

In the following sections we well explain in more

detail all algebra operators and algebra relational.

The algebra operators are based on W3C (standard

algebra) and comprise XML-specific and special

operations.

4 OUR XML DATA MODEL

Figure 1 shows an XML tree, in which there is a

topmost, unique element, collection, known as the

root of the XML document (ancestor) (Comon et al

1997). All elements are enclosed within Х&topmost

element, collection. Object1 and object3 sub-

elements reside within the root node. This nesting of

sub-elements can go to an arbitrary level. Figure 1

shows the tree data model.

Elements and attributes correspond to nodes in the

XML tree. Directed, named edges connect nodes,

with the tag of the corresponding element or

attribute name acting as the name of an edge. For

each node of the tree, except the root node, there is a

backward edge leading to the parent node. Note that

a parent node appears only between those connected

with child nodes or leaf nodes. A path consists of the

sequence of node names that one needs to follow in

order to arrive at a node from the root node.

4.1 Concepts in the tree model

Root (ancestor or parent): the top node of the tree is

identified as the root node.

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

306

ad : (ancestor - descendent)

pc : (parent - child)

co lle ctio n

object1

object3

objid

ob jectInfo r2

des_date

016

F_format

referenceinfo

Doc:

objectInfor1

objNum ber

100 1234

Info _ id

10 12.10.98

Info _ id

des_date

20 12.12.98

objectInfor4

des_date

objectIn fo r3

objNum ber

3239

Info _ id

03 12.10.99

Info _ id

des_date

09 12.12.99

objid

301

im ageinfor

Im g_ id

ref_id

title

typ e

pdf r35

co lle to r

bibliographic

Elem ent Edge

Parent Edge

– Node (parent or child): an edge is a link from a

parent node to a successor node, called child

node.

Figure 1: Tree data model

– Leaf (child): child nodes, atomic values

– Path: a path from node V1 to Vn sequence of

nodes, where 1<=n<=20

– Descendants: represent all nodes that are

children of current node or children of children

of current node and so on.

– Ancestor of nodes V are parent, grandparent, etc,

that is all nodes found on the path from node V

to the root node. The ancestor represents all

nodes that are parent of current node or parent of

parent of current node and so on.

4.2 XML Document as Tree Structure

– XML document → Tree

– Element → Root node, parent, child node

– Leaf → child node, atomic values

– Attribute → function, values.

5 ALGEBRA RELATIONAL

In this section we introduce four types of relational

algebra operators: Universal, Similarity,

Equivalence and Subsumption. In the following

sections we will explain these relations in more

details.

5.1 Universal Element Relation

This relation is unary (∪) and contains all

information. In a case study for a museum objects

information system the universal element would

include the collections, their objects, object

information and exhibition and institutions as

described in (ICOM 1995, CIDOC 2002) and

presented by Ali Elbekai in his thesis.

5.2 Similarity Relation

Similarity relation (∼) means that the major

structures of the two trees are similar, for example

the Doc4 tree is similar to the Doc3 tree, as in Figure

2. Also, the similarity relation is a binary relation. In

general we can see the relation between any two

XML tree is similarity if the following holds: the

root node in Doc

n tree and the root node in Docm

tree are similar, the parent node in Doc

n tree and the

parent node in Doc

m tree are similar and the child

nodes in the Doc

n tree and the child node in Docm

tree are similar. In addition if we find that any parent

node or child node in Doc

n tree or Docm tree is an

unnamed node then this node matches the

corresponding named node at the same level and

position as are depicted in Figure 2.

5.3 Equivalence Relation

Equivalence relation (≈) means that two trees are

indistinguishable as in Figure 3 where the nodes in

the Doc3 tree are equivalent to those in the Doc4

tree then we can identify that the Doc3 tree is

equivalent to the Doc4 tree. The equivalence relation

is a binary relation. In general we can explore that

the relation is equivalence between any two XML

trees if the following holds: the root node Doc

n tree

and the root node Doc

m tree are equivalent, the

collection4

Doc4

objectInfor2

12.10.98

collection3

12.12.98

Info_id

desc_date

Doc3

object3

objectInfor1

Info_id desc_date

objectInfor2

10 12.10.98

12.12.98

Info_id

desc_date

object3

objectInfor1

Info_id

desc_date

object1

Figure 2: Similarity relational operator

A TREE BASED ALGEBRA FRAMEWORK FOR XML DATA SYSTEMS

307

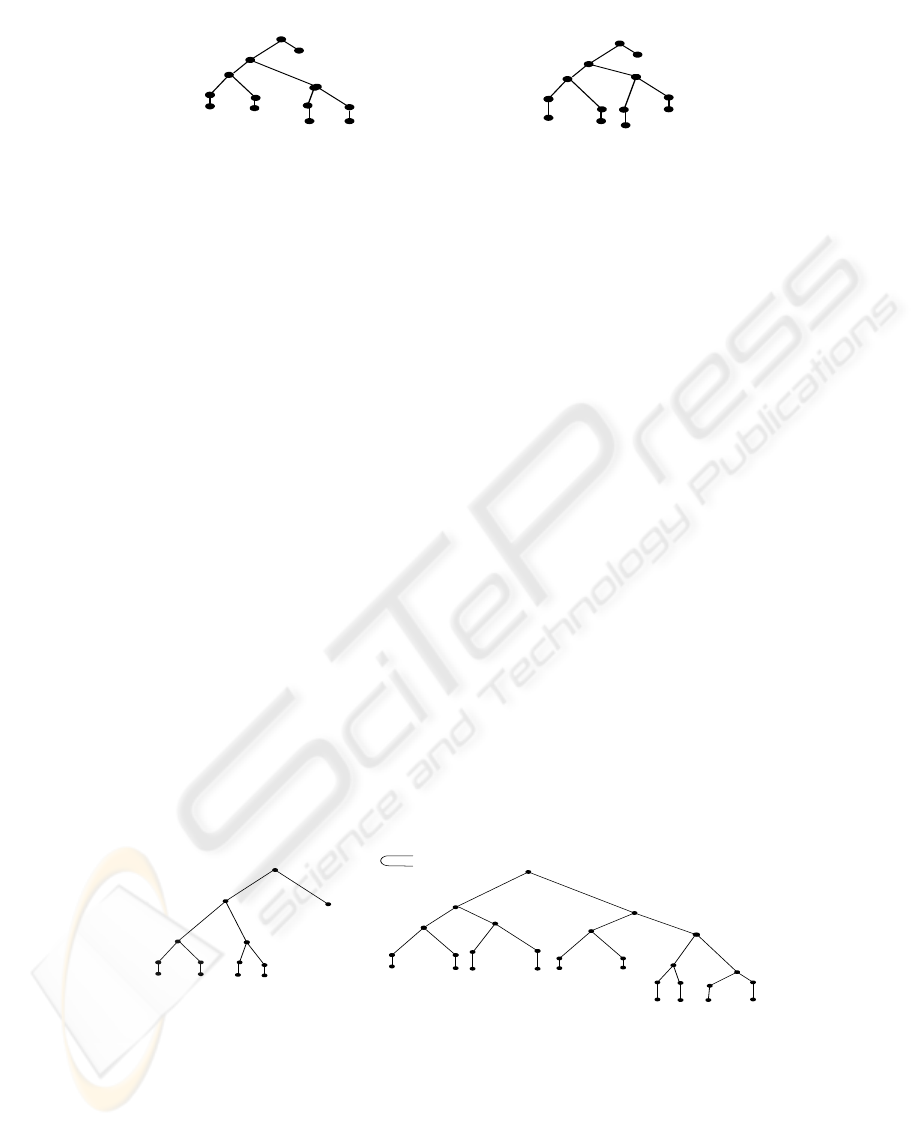
parent node Docn tree with parent node Docm tree

are equivalent and the chid nodes Doc

n tree and

child nodes Doc

m tree are equivalent. In addition if

the parent node or child node in both Doc trees is

unnamed, then the unnamed node matches the

corresponding node in the same level and position.

collection3

Doc3

objectInfor2

12.10.98

collection4

12.12.98Info_id

desc_date

Doc4

object3

objectInfo r1

Info_id desc_date

objectInfor2

10 12.10.98

12.12.98

Info_id

desc_date

object3

objectInfor1

Info_id

desc_date

object1

Figure 3: An Equivalence relational operator

5.4 Subsumption Relation

Subsumption (⊂) means that one tree is a subset of

the other, for example the Doc3 tree is a subset of

the Doc1 tree in a binary relationship. If the nodes

present in Doc3 tree are a subset of the nodes

present in Doc1 tree then we can see the Doc3 tree is

a subsumption of the Doc1 tree. In general we can

conclude that the Doc

n tree is subsumption or equal

of Doc

m tree if the following holds: the root node

Doc

n tree exists in Docm tree, the parent node Docn

tree exists in the Doc

m tree and the child node Docn

tree exists in the Doc

m tree. In other words the Docn

tree is part of Doc

m tree.

6 ALGEBRA OPERATORS

All operators in tree algebra take one tree or more as

input and produce one tree of data as output (Roth,

Korth & Silberschatz 1988).

6.1 Join Operator

A join (⊕) is a binary operator, which takes two

trees as input, and combines them into one tree as

output. This combination is made whenever a certain

expression holds true, that is the two tree collections

are joined on a predicate. The predicate can be as

generic as the conditions accepted by the selection

operator. The query operation selects documents that

meet the stated criteria from a collection of

documents. It may also extract components from

selected documents and construct new documents

from these components. Also the join operator has

the property of being commutative. More precisely

Doc1 tree ⊕ Doc2 tree = Doc2 tree ⊕ Doc1 tree.

Furthermore, it is associative which means (Doc1

tree ⊕ Doc2 tree) ⊕ Doc3 tree =Doc1 tree ⊕ (Doc2

tree ⊕ Doc3 tree). Figure 5 shows how to join any

two trees in general. The syntax of the join operator

is DOCn Tree ⋈ [condition] DOCm Tree

where(1<=n<=10) and (1<= m< = 10)

object3

objectInfo r2

objectInfor1

12.10.98

Info_id

desc_date

collection3

20 12.12.98

Info_id

desc_date

Doc 3

collection1

object1

object3

objectIn fo r2

desc_date

form a t

referenceinfo

Doc1

objectInfo r1

Info_id

12.10.98

Info _id

desc_date

12.12.98

objectIn fo r4

desc_date

objectInfo r3

Info_id

12.10.99

im ageinfor

Im g_id

ref_id

typ e

pdf r35 Bibliographic

object1

Figure 4: Subsumption relational operator

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

308

// Input two XML document or two DOC tree (DOCn, DOCm)

// Output DOCnm Tree = (DOCn Tree ⊕ DOCm Tree)

1. start from root node DOCn tree and root node DOCm tree

2. if root node has parent\child node

2.1 perform depth-first algorithm

2.2 if the parent node DOCn tree has child node and parent node DOCm tree has child node

2.2.1 While child node DOCn tree agrees with child node DOCm tree repeat:

2.2.1.1 join such child node (concatenation without repetition)

2.2.1.2 set the output in DOCnm tree

2.2.1.3 if child node in DOCn tree has leaf node agree with leaf node DOCm tree

2.2.1.3.1 join such leaf node (concatenation without repetition)

2.2.1.3.2 set joined leaf node to the output DOCnm tree

2.2.1.4 join such leaf node in DOCn tree to leaf node DOCm tree

2.3 set parent node to DOCnm tree

3. set no parent/child node and root node into DOCnm tree and terminate

4. end/terminate

Figure 5: An algorithm for Joining of two XML documents or two Doc trees

// Input two XML document or two DOC tree (DOCn Tree, DOCm Tree)

// Output DOCnm Tree = (DOCn Tree ∪ DOCm Tree)

1. start with root node DOCn Tree and root node DOCm Tree

2. set root node DOCn Tree or root node DOCm Tree in new DOCnm Tree

3. if root node has parent/child node in either DOC Tree

3.1 perform depth-first algorithm

3.2 if the parent node DOCn Tree = parent node DOCm Tree

3.2.1 set parent node DOCn Tree or DOCm Tree in new DOCnm Tree

3.2.2 while parent node DOCn Tree has child node or parent node

DOCm Tree has child node

3.2.2.1 set child node to new DOCnm Tree

3.2.2.2 eliminate duplicate child node

3.2.3 repeat

3.3 set null to new DOCnm and terminate

4. set null and terminate

Figure 6: An algorithm for Union two XML documents or two Doc Trees

6.2 Union Operator

The purpose of the Union operator (∪) is to union

two XML trees. It is a binary operator with two

XML trees as input and one XML tree as output.

This is depicted in Figure 6. Furthermore, the union

operator is commutative. More precisely, DOC1 tree

∪ DOC2 tree = DOC2 tree ∪ DOC1 tree. Also it is

an associative operator, meaning

that (DOC1 tree ∪ DOC2 tree) ∪ DOC3 tree =

DOC1 tree ∪ (DOC2 tree ∪ DOC3 tree).

Furthermore the output of the union operators is new

XML tree data containing all the elements, root

node, parent nodes and child nodes in the two input

Doc trees data model without the duplication of any

elements such as root nodes, parent nodes and child

nodes. In general the syntax of the union is DOCn

Tree ∪ DOCm Tree, with limits (1<=n<=10) and

(1<=m<=10). The union is disjoint: duplicates are

purged.

6.3 Complement Operator

The complement operator (⊥), as a binary operator,

operates on two XML trees as input, and produces

one XML document or one XML tree as an output.

In other words the XML document is a tree; the

result of the complement of the two DOC trees is a

new DOC tree containing all the nodes present in the

first input DOC tree but not in the second DOC tree.

That is the output of the complement operator is a

new XML tree containing all element nodes (root

node, parent nodes, children nodes, function, values)

existing in the input DOCn tree data model and not

existing in the DOCm tree. Figure 7 show how we

can complement the two DOC trees or two XML

document in general.

A TREE BASED ALGEBRA FRAMEWORK FOR XML DATA SYSTEMS

309

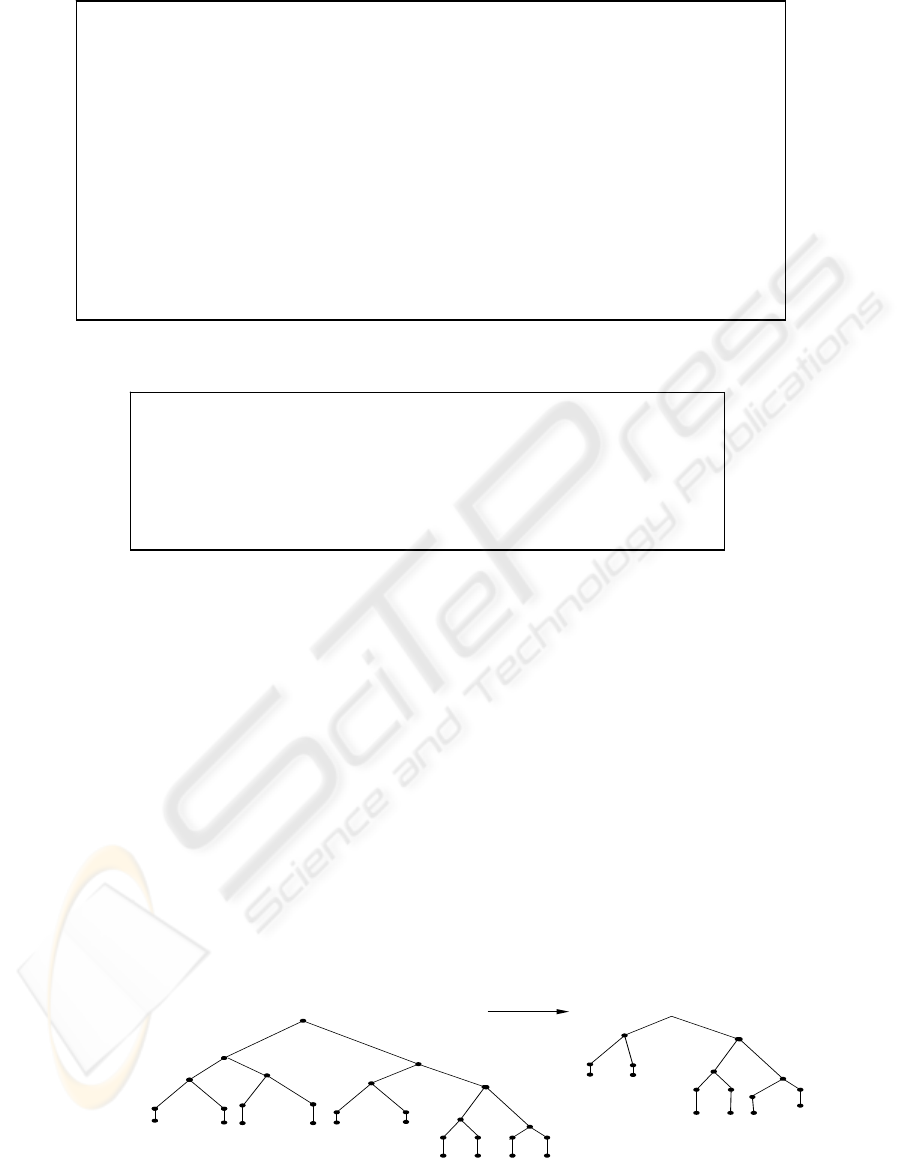
// Input two XML document or two DOC tree (DOCn Tree, DOCm Tree)

// Output DOCnm Tree = (DOCn Tree - DOCm Tree)

1. start from root node DOCn

2. If root node DOCn Tree and root node DOCm Tree has parent/child node

2.1 Perform depth-first algorithm

2.2 if DOCn Tree has parent node not existing in DOCm Tree

2.2.1 set parent node DOCn Tree to the new DOCnm Tree

2.2.2 while parent node DOCn Tree has child node not existing in DOCm Tree

2.2.2.1 set child node DOCn Tree to DOCnm Tree

2.2.2.2 if child node DOCn Tree has leaf node not existing in DOCm Tree

2.2.2.2.1 set leaf node DOCn Tree to DOCnm Tree

2.2.2.3 set null to DOCnm Tree

2.2.3 repeat

2.3 set null to DOCnm Tree

3. set root node to DOCnm Tree and terminate

4. end/terminate

Figure 7: An algorithm for Complement two XML documents or two Doc Trees

// Input one DOC tree and the Output one DOC tree

1. start from the root node of DOC Tree

2. if root node has parent/child node

2.1 Perform depth-first algorithm

2.2 if projected node/selected node is equal to current node

2.2.1 set the projected node as output to new DOC Tree

2.3 node projected/selected not exist and terminate

3 end/terminate

Figure 8: An algorithm for Projection operator

The purpose of the complement operator is to

compute the difference between the two input trees:

DOCn Tree - DOCm Tree with limits (1<=n<=10)

and (1<=m<=10). The complement operator is not

commutative, which means DOC1 tree – DOC3 tree

≠ DOC3 tree – DOC1 tree. Also it is not an

associative operator.

6.4 Projection Operator

The input for the projection operator (π) is one XML

tree, as it is unary. In general Figure 8 shows how

the projection operator works on nodes of the DOC

tree or elements of the XML document.

As can be seen from Figure 9 we take object3 as a

parameter and the searching is performed on the root

node collection1 in Doc1 tree. The output of the

projection operator is a new XML document or new

DOC1p tree. For trees, projection may be regarded

as eliminating nodes other than those specified. In

the substructure resulting from node elimination, we

would expect the (partial)

hierarchical relationship between surviving nodes

that existed in the input collection to be preserved.

Projection in tree algebra takes one collection <C>

(tree) as input and as parameters. Projection

starts the search at the root node and follows the

path parent node successor, the child node, until it

finds the node projected. The syntax of the

projection operator is defined as follows: π<C>

where is parameter and <C> is tree.

co lle c tio n 1

object1

object3

ob je ctIn fo r2

desc_date

form a t

referenceinfo

Doc1

ob je ctIn fo r1

10 12.10.98

In fo _ id

desc_date

12.12.98

o b je c tIn fo r4

desc_date

objectInfor3

Info _ id

12.10.99

imageinfor

Im g _ id

ref_id

typ e

pdf

r35

Bibliographic

fo rm at

referen ceinfo

o b je c tIn fo r4

desc_date

ob je c tIn fo r3

Info _ id

12.10.99

imageinfor

Im g _ id

ref_id

typ e

pdf r35

Bibliographic

object3

Doc1p

Info_id

Figure 9: An example for Projection operator

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

310

// Input one DOC tree or one XML document

// Output one DOC tree or one XML document

1. start with entry point, it is the root node

2. perform depth-first algorithm

2.1 if parameter is equal the specific node needed to expose

2.1.1 return the specific node

2.1.2 set specific node in the new tree

2.2 exposed element not exist and terminate

3. end/terminate

Figure 10: An algorithm for exposing specific node of Doc tree

6.5 Select Operator

The purpose of a select (σ) operation is to filter out

tuples in the XML algebra satisfying an expression

given as a predicate. The select operator is a unary

operator to take one XML document or one tree as

input and produce one XML document or one tree as

output. The selection operator allows us to

determine a subset over a collection of documents. It

applies a given condition to each member of the

collection of nodes and returns a result node or

collection of nodes consisting of those members for

which the condition evaluates true. Selection in tree

algebra takes tree as input, and a as parameter,

and returns an output tree <C>. Formally, the syntax

of select is defined as follows: σ

<C>. The

result of selection is a tree. We can take the

parameter and start our selection by depth-first from

the root node of the XML tree and successor, the

parent nodes and successor child nodes until the

selection condition is satisfied.

6.6 Expose/Vertex Operators

The Expose operator (ε) has one XML document or

one Doc tree as input, as it is a unary operator and

produces one Doc tree as the output. The purpose of

the Expose operator is to retrieve specific elements

of the XML document or specific nodes of the Doc

tree. The Expose operator accepts as its parameters

a list of path expression to be exposed from the

document on which it operates, with the path

expression in entry-point notation. Figure 10 shows

how we can expose specific nodes of the Doc tree in

general.

The Expose operator accepts as its parameter the

element (parent, child) exposed from the tree data

model on which it operates, with the path in entry

point notation, and follows the path root node,

parent node and successor child nodes until the

element required to be exposed is found. The output

of an Expose operator imposes a new ordering, the

same as the order of its arguments. Once the nodes

denoted by the path are reached, a

new element content is constructed. In general the

new syntax of the expose operation is:

Expose[edge1<element>](element: expression)

The Vertex operator (ν) has one XML document or

Doc tree as input, as it is a unary operator, and

creates the actual XML vertex that will encompass

everything created by the Expose operator. It

arranges the element content according to the order

indicated by its input. It creates the XML to which

nodes can be connected, as well as the named edges

that lead to the newly defined tree.

7 DISCUSSION

The results from our literature review gave us a

choice of an existing solution for applications in our

context of either (1) Lore algebra, adopting an

existing standard for building an original solution,

(2) the standard XML algebra of W3C, or (3)

developing a more targeted solution, that is a domain

specific algebra, to handle our requirements. All the

considerations, given earlier in the review, have

already been taken into account by the team working

on the standard XML algebra (W3C February 2001)

and XQuery (W3C 2004). In fact, the standard

algebra is largely based on the AT&T model with

some additional features and revisions in the spirit of

Niagara. So, the standard is a satisfactory starting

point for us in our efforts to develop domain specific

algebra and was therefore adopted as the basis for

our way forward. However, it does not make sense

to implement the full algebra defined by the standard

for one single specific task or even for a class of

similar tasks. Because of this we have developed a

formal data model as a restricted version of the

universal algebra suitable for a representative class

of problems. Of course, such an approach may lead

to a non-universal model, but at the same time, it is

feasible and does produce a more effective solution

for particular classes of problems. On this basis, we

started with the XML Schema (W3C September

2001) of the data to develop domain specific XML

algebra more suitable for data processing of the

specific data and then we used it for implementing

the main offline components of the system. There

are two types of operators in our algebra: firstly, the

algebraic operators are join, union, complement,

A TREE BASED ALGEBRA FRAMEWORK FOR XML DATA SYSTEMS

311

project, select, expose and vertex. Every operator

outputs a tree, which makes it distinct from other

algebra operators. Secondly, the relational operators

are universal, subsuming, equivalence, and

similarity. This means our work is based on the tree

based algebra framework for XML data systems.

Also, our algebra has a sound data structure and a

simple representation of the data. A contribution of

this work is that it introduces an algebra that

operates on a new data model, because our algebra

employs XML trees as data sources and targets. Our

algebra framework can be used in integrated

architectures for distributed information processing

and its components will be XML schema driven.

Furthermore, as a test framework for our integrated

approach we will prototype a system for the

exchange of information between several

independent museums for organising virtual

exhibitions over the Web. Also, we plan to extend

the algebra to support some of the more advanced

features of the XML query language.

REFERENCES

Beech, D, Malhotra A, & Rys, M, (eds.) A formal data

model and algebra for XML, Comm W3C (1999).

Bourret, Ronald. XML and Database (2004) at:

http://www.rpbourret.com/xml/XMLAndDatabases.ht

Christophides, V, Cluet, S & Simeon, J, On wrapping,

query languages and efficient XML integration, ACM

SIGMOD Conf Management Data, Dallas 141-152,

May (2000).

CIDOC Group (July 2002)

http://www.willpowerinfo.myby.co.uk/cidoc/cidoc0.ht

Codd, E F, Relational Completeness of Data Base, Data

Base Systems, Prentice Hall 6 65-98. (1972).

Comon, H, Dauchet, M, Gilleron, R, Jacquemand, F,

Lugiez, D, Tison, S, & Tommasi, S, Tree Automata

Techniques and Applications, at:

http://www.grappa.lille3.fr/tata. (1997)

Fenkhauser, M, Simeon, J, & Woder, P, An algebra for

XML Query, In Proc. FST TCS, New Delhi,

December (2000).

Fernandez, M, Simeon, J, & Wadler, P, A semi-monad for

semi-structured data, Int Conf Database Theory 263-

300 (2001).

Galanis, L, Viglas, E, DeWitt, D J, Naughton, J F, &

Maier, D, Following the paths of XML Data: An

Algebraic Framework for XML Query Evaluation,

Tech Rep Univ Wisconsin (2001).

Greenwald, M B, Moore, J T, Pierce, B C, Schmitt, A:

Language for Bi-Directional Tree Transformations.

Tech Rep MS-CIS-03-08, Dept Comp Inf Sci, Univ

Pennsylvania. (Aug 2003).

ICOM, International Guidelines for Museum Object

Information (IGMO): CIDOC Information Categories

(October (1995) http://www.cidoc.icom.org/guide

McHugh, J, Abiteboul, S, Goldman, R, Quass, D, &

Widom, J, Lore: A Database Management System for

Semi-structured Data. SIGMOD 3(26) 54-66 (1997).

McHugh, J, & Widom, J, Query optimization for Semi-

structured data, Tech Rep, Stanford Univ Database

Group, August (1998).

http://www-db.standford.edu/pub/papers/qo.ps.

Roth, M A, Korth, H F, & Silberschatz, A,

Extended

algebra and calculus for nested relational databases,

ACM TODS

13 389-417 (1988).

Scholl, M H, Theoretical foundations of algebraic

optimization utilization unnormalized relation, in:

ICDT’86, LNCS 234 409-420. (1986).

W3C, the XML Query Algebra, Working Draft,

http://www.w3.org/TR/2001/WD-query-algebra-

20010215. February (2001).

W3C, XML Schema: Formal Description, Working Draft,

September (2001).

W3C, XQuery 1.0: An XML Query Language, Working

Draft (23 July 2004)

http://www.w3.org/TR/2004/WD-xquery-20040723/

Zhang, X. and Rundensteiner, E A, XML Algebra for the

Rainbow System, Tech Rep WPI-CS-TR-02-24.

Worcester Polytechnic Inst, July (2002).

Zisman, A, An Overview of XML, Comp Control Eng J

11(4) (2000).

ICEIS 2005 - DATABASES AND INFORMATION SYSTEMS INTEGRATION

312