
Combining Multiple Pairwise Neural Networks
Classifiers: A Comparative Study
Olivier Lezoray
1
and Hubert Cardot
2
1
LUSAC (EA 2607), groupe Vision et Analyse d’Image, IUT Dpt. SRC, 120 Rue de l’exode,
Saint-L
ˆ
o, F-50000, France
2
Universit
´
e Francois-Rabelais de Tours, Laboratoire d’Informatique (EA 2101), 64 Avenue
Jean Portalis, Tours, F-37200, France
Abstract. Classifier combination constitutes an interesting approach when solv-
ing multiclass classification problems. We review standard methods used to de-
code the decomposition generated by a one-against-one approach. New decoding
methods are proposed and are compared to standard methods. A stacking decod-
ing is also proposed and consists in replacing the whole decoding by a trainable
classifier to arbiter among the conflicting predictions of the binary classifiers.
Substantial gain is obtained on all datasets used in the experiments.
1 Introduction
Since the advent of data mining in information management systems, the applications
of multiclass pattern recognition has covered a very wide range including image or text
categorization, object classification, speech recognition. Multiclass pattern recognition
aims at building a function F that maps the input feature space to an output space
of more than two classes. Each example (x, y) consists of an instance x ∈ X and a
label y ∈ {1, ..., K} where X is the feature vector input space and K the number
of classes to be discriminated. A general classifier can be considered as a mapping F
from instances to labels F : X → {1, ..., K}. There are two ways for a classifier to
solve multiclass problems: (1) consider all the data in one optimization problem, (2)
construct several binary classifiers and combine them. The first approach formulates
the multiclass problem into one single optimization problem (all-at-once). However
the number of samples is the main factor that contributes to the time complexity for
training the classifier, therefore algorithms of the first category are significantly slower
that the ones that include several binary classifiers where each classifier classifies only
a small portion of the data [1–4]. Moreover, muticlass classification is intrinsically
harder than binary classification because the classification algorithm has to learn to
construct a high number of separation boundaries whereas binary classifiers have to
determine only one appropriate decision function. Currently, a common approach to
construct a multiclass classifier relies in decomposing the multiclass problem into a set
of binary ones and then combining their outputs to make a final multi-class prediction
[2,5]. The basic idea behind combining binary classifiers is to decompose the multiclass
problem into a set of easier and more accessible binary problems. The main advantage
Lezoray O. and Cardot H. (2005).
Combining Multiple Pairwise Neural Networks Classifiers: A Comparative Study.
In Proceedings of the 1st International Workshop on Artificial Neural Networks and Intelligent Information Processing, pages 52-61
DOI: 10.5220/0001193700520061
Copyright
c
SciTePress

in this divide-and-conquer strategy is that any binary classification algorithm can be
used. A binary classifier having to face with the classification of data using examples
as positive ones and the others as negative ones, there are two schemes to construct
several binary classifiers for multiclass (K-class) problems [6]. The most traditional
scheme (the standard method) [7] builds K different classifiers. A separate concept is
modeled by each classifier by defining a separate learning problem for each class. The
original problem is split into a series of binary problems (one for each class) where
the i
th
classifier is trained while labeling all the samples in the i
th
class as positive
and the rest as negative. This technique is called one-against-all since each classifier
separates one class from all the others. The drawbacks of this approach is that each
binary classifier has to see all the training database and not a reduced version of it and
the training data can be unbalanced which can distort each binary classifier. The second
scheme constucts K × (K − 1)/2 classifiers using all the pairwise combinations of
the K classes [4,8,9]. This technique is called one-against-one. The latter approach
is very interesting since the binary decision not only contain fewer training examples
but the decision function of each binary problem can be considerably simpler than in
the case of one-against-all binarization since the classes have less overlap [1,2]. The
major advantage of this approach is that it provides redundancy which can lead to better
generalization abilities.
Beside choosing the way to decompose the problem, one also needs to devise a
strategy for combining the binary classifiers and provide a final prediction, namely how
to combine the outputs provided by all the binary classifiers. This is of importance to
define a multiclass classifier from several binary ones. Whatever the used decomposi-
tion (one-against-all and one-against-one) if a simple voting strategy is used, there can
be inconsistent regions [9] (less for one-against-one but still remain). For one-against-
all the classifiers might all consider the input as not being of their class or several ones
can conclude that it is of their class. For one-against-one, all the classifiers can disagree.
The problem of combining binary classifiers has therefore been extensively studied and
a lot of combining scheme have been proposed but many researchers reported opposing
views to which scheme is better in terms of accuracy and speed [1,2, 6–16]. Speed
issues depend primarily on the different implementations of the basic binary classifier
and accuracy issues depend on the nature of the basic learner, the data set and how the
basic classifiers are well tuned to achieve maximum performance [7]. The litterature
being inconclusive, the best method for combining binary classifiers is an important re-
search issue which remains open. In this paper we propose to compare several classical
combining schemes using multi layer perceptrons as the base learner, moreover we also
propose new combining schemes which outperform the classical ones. We consider
only the one-against-one formulation to proceed to the construction of binary neural
networks. In section 2 we present the binary neural networks we used and in section
3 we discuss how to combine binary neural networks. In section 4 we demonstrate the
effectiveness of the proposed combining methods by computer experiments.
53

2 Binary Neural Networks
Since we consider the one-against-one decomposition scheme, for a classification prob-
lem with K classes, a set of networks is built, each one being in charge of sepa-
rating elements from two distinct classes. The set of different classes is denoted by
C = {C
1
, C
2
, ..., C
K
} and |C| = K. For K classes, that leads to have (K ×(K −1))/2
neural networks being used for classification (denoted as MLP for Multi Layer Percep-
trons). The set of Binary Neural Networks (BNN) is given by A = {R
C
1
,C
2
; · · · ; R
C
K−1
,C
K
}.
The difficulty in separating K classes all-at-once is simplified by the specialization of
each network, because a network is interested only in the separation of two classes.
When one of these neural networks learns how to differentiate two classes, only the ob-
jects belonging to these two classes are presented to the neural network. This implies,
on the one hand to simplify the training (since the set of data to be learned is restricted)
and on the other hand, to make easier the discrimination between these two classes since
the network learnt how to recognize only those [17]. The global training dataset con-
taining patterns of all the different classes is denoted by D
T rain
. The latter is divided
in several subsets for each neural network. D
T rain
(C
i
, C
j
) is the dataset which corre-
sponds to the neural network which differenciates the classes C
i
and C
j
and contains
patterns of only those two classes. The initial training data (D
T rain
(C
i
, C
j
)) associ-
ated to each neural network is split into two subsets: a learning set (D
Learn
(C
i
, C
j
))
and a validation set (D
V alid
(C
i
, C
j
)). The learning of a neural network is performed
on D
Learn
C
i
, C
j
) and the D
V alid
(C
i
, C
j
) validation set is used to evaluate the classi-
fication rate of the network during the training. Therefore the validation set is not used
to learn the weights of neural networks, only to tune the hyperparameters (number of
neurons, number of iterations, ...). The structure of the neural networks used is the fol-
lowing one: a layer of inputs containing as many neurons as the number of attributes
associated with the object to be classified, a hidden layer containing a variable number
of neurons and one output neuron. The value of the output neuron is in the interval
]− 1, 1[. According to the sign of the result associated with this single neuron, an object
is classified in one of the two classes that the network separates. The neural networks
used by our architecture are very simple (only one hidden layer, only one neuron of
output). This has several advantages [3,10, 18]. The simplicity of the task associated
to each neural network simplifies the convergence of the training as well as the search
for a simple structure. The generalization of their structure can be made in a dynamic
way very easily. Therefore, an automatic method is used to find the number of hidden
neurons that gives the best classification rate [3,19,20]. The output value provided by
a BNN when a sample data x has to be classified is denoted by O(x, R
C
i
,C
j
). From
this output, x can be classified as C
i
or C
j
according to the sign of the output: x is
considered as of class C
i
if O(x, R
C
i
,C
j
) ≥ 0 and C
j
otherwise. The output can there-
fore be directly used as an estimate for the class memberships. However it might be
more suitable to have pairwise class probability estimates which can be obtained by [4]
r
ij
(x) = (O(x, R
C
i
,C
j
) + 1)/2 and r
ji
(x) = 1 − r
ij
(x). r
ij
(x) gives the pairwise
posterior probability of the input vector x to belong to the class i and r
ji
(x) to the class
j (according to the single BNN R
C
i
,C
j
).
54

3 Combining binary classifiers
Constructing multiclass classifiers from a pairwise decomposition consists in combin-
ing the B = (K × (K − 1)/2) pairwise classifiers outputs. Each binary classifier is
a mapping f
b
: X → R with b ∈ {1, ..., B}. A vector f(x) = (f
1
(x), ..., f
B
(x))
is constructed from the outputs of the binary classifiers. A combination rule g can
then be applied to combine all the outputs f (x) = (f
1
(x), ..., f
B
(x)) using a function
g : R
B
→ R
K
which couples the estimates of each binary classifier in order to obtain
class membership estimates (which can be probabilities) for the multi-class problem.
Once the class memberships µ have been estimated g(f(x)) = g(f
1
(x), ..., f
B
(x)) =
(µ(C
1
|x), ..., µ(C
K
|x)), a final selection scheme is used to choose the winner class.
This is done as a mapping h : R
K
→ {1, ..., K}. The whole K-ary classifier com-
bining all the binary classifiers scores (obtained by pairwise decomposition) is denoted
by F (x) = h(g(f(x))) where h is the selection scheme function applied to select the
winner class ang g the combination rule. h ◦ g defines the complete decoding scheme
needed to perform multiclass classification from binary pairwise classifiers.
3.1 Standard Decoding
To obtain class membership estimates from the BNN outputs, a combination rule g is
needed to perform the decoding. This rule associates a vector of BNN outputs f(x)
with a vector of class membership estimates g(f(x)) = (µ(C
1
|x), ..., µ(C
K
|x)). In
this section we review the classical combination rules that can be used to that aim and
propose new ones.
Majority vote The most commonly used combination rule is probably the Majority
Vote (MV) one. With this combination rule [21], each class receives votes from in-
dividual classifiers. The membership estimates correspond to the number of votes re-
ceived by each class. µ(C
i
|x) = Σ
j
V (r
ij
(x) ≥ 0.5) with V (x) = 1 if x is true and 0
otherwise. The chosen class is the one which receives the largest number of votes) and
h = argmax.
Hastie A way to obtain class membership estimates from the pairwise probability esti-
mates r
ij
(x) has been proposed by Hastie [8]. To combine all the estimates of the BNNs
we would like to obtain a set of class membership probabilities p
i
(x) = P (C
i
|x). The
r
ij
are related to the p
i
according to r
ij
(x) =
p
i
(x)
p
i
(x)+p
j
(x)
. In order to find the best
approximation r
′
ij
=
µ
i
(x)
µ
i
(x)+µ
j
(x)
the algorithm starts with µ
i
(x) =
2Σ
j6=i
r
ij
(x)
K(K−1)
and
computes the corresponding r
′
ij
(x). The µ
i
(x) are obtained by minimizing the aver-
age Kullback-Leibler distance between r
ij
(x) and r
′
ij
(x). At convergence we have the
class membership estimates with µ(C
i
|x) = µ
i
(x). The winner class is considered as
the most likely one and h = argmax.
Price Another approach for estimating the class memberships has been proposed by
Price [4]. It is based on the fact that neural networks trained to minimize a MSE
55

cost function estimate posterior probabilities. A BNN with sigmoidal transfer func-
tion can compute the posterior probabilities for the two classes (previously denoted
by r
ij
(x) and r
ji
(x)). One can then obtain the final expression of the class member-
ship by: µ(C
i
|x) =
1
Σ
j6=i
1
r
ij
(x)
−(K−2)
. As for the Hastie combination rule, we have
h = argmax.
ECOC Another interesting combination rule is based on Error Correcting Output
Codes (ECOC) [11,22]. It has been introduced to combine the outputs of binary
Support Vector Machines. For a problem with K classes, it creates a matrix M ∈
{−1, 0, 1}
K×B
. A column in the matrix M corresponds to a binary classifier R
i,j
and
a row corresponds to a class. For instance the first column corresponds to the classi-
fier R
1,2
and it learns to recognize the classes 1 and 2 (respectively the +1 and −1
coefficients of the column, the other coefficients are set to 0 since the classifier does
not differentiate the other classes). Combining all the binary classifiers to estimate the
class memberships consists in comparing the matrix rows with the classifiers outputs
expressed by : µ(C
k
|x) =
P
B
b=1
L(M(k, b).f
b
(x)). This provides the distortion be-
tween the vector of the BNN outputs f(x) and the row M (k, ·). For this combination
rule the outputs of the binary classifiers O(x, R
ij
) are directly used and not the r
ij
(x).
We used Loss Based decoding and have set L(z) = exp(−z). For ECOC decoding
schemes h = argmin since this leads to find the row being the most similar to the
classifiers outputs [23,24].
Min-Max For all the previous decoding schemes, the probability estimates of the clas-
sifiers obtained by the combination rule g are used to assign to an input pattern the class
with the maximal output. Combining all the pairwise classifiers can lead to bad results
since if the input x is of class C
i
, there are only (K − 1) relevant classifiers among the
(K ×(K −1))/2 which have seen the class C
i
and the remaining ((K −1)×(K −2))/2
irrelevant classifiers have never seen inputs from class C
i
. While classifying an input
one whishes that relevant classifiers will provide coherent informations to cope with all
the irrelevant ones. To try to alleviate this problem, we propose to get the minimum
value of r
ij
(x) for each class C
i
: µ(C
i
|x) =
K−1
min
j
r
ij
(x). Finally we select the class
which maximizes this minimum value: h = argmax. The principle of this method
consist in choosing the candidate class whose probability is less bad than that for all
other candidate classes. The intuitive idea behind is that having a high pairwise proba-
bility for a particular pair of classes does not imply a strong decision towards this class
because of irrelevant classifiers. However it can be rejected if the probability is low.
3.2 Elimination Decoding
Another decoding scheme is the elimination decoding one. This decoder was origi-
nally described by Kressel [5] and reintroduced by Platt [12] where it was called
Directed Acyclic Graph (DAG). One strong argument for using DAG is that it resolves
the problem of unclassifiable regions for pairwise classification. The elimination decod-
ing is nothing more than a decision-tree based pairwise classification. Two sets are used
56

where |.| stands for Card(.). The set of binary classifiers A
0
= {R
1,2
, ..., R
K−1,K
}
(with |A
0
| = B) contains all the binary classifiers and the set E
0
= {C
1
, ..., C
K
} (with
|E
0
| = K) contains all the candidate winner classes. Elimination decoding operates
iteratively. At each iteration t = {1, ..., K − 1}, the size of E
t
is decreased by one (one
class C
k
is eliminated) and all the classifiers discriminating C
k
in A
t
are eliminated
[24]: A
t+1
= A
t
− {R
i,j
: i = C
k
∨ j = C
k
}. The set A
K−2
contains only one
binary classifier which determines the winner class. Several problems occur however
when using DAGs. First of all the choice of the winner class depends on the sequence
of binary classifiers in nodes which affects the reliability of the algorithm. Moreover
the correct class to be predicted is more or less advantaged according to its distance to
the root node (higher risk of being rejected in the nodes near the root). Secondly since
there are a lot of classifiers which are irrelevant for a given classification, using these
classifiers can cause severe defects. To overcome this problem, several authors have
proposed to use an adaptative DAG by optimizing its structure, however the general-
ization ability still depends on the structure of the tree [10, 18, 25–27]. We propose a
new elimination decoding which takes into account all the outputs of the binary clas-
sifiers. When using a classical decoding scheme without elimination, one selects the
class with the largest probability (h = argmax). In the case of elimination, we want
to eliminate the least credible class and this comes back to eliminate the class hav-
ing the minimum of probability. The class to be eliminated is deduced from the class
membership estimates : C
k
= h(g(f (x))). g can be anyone of the previous combina-
tion rules (MV, Price, Hastie, Max) and since the method eliminates the least probable
class at each iteration, we have h = argmin. At the iteration t, the number of candi-
date classes is |E
t
| = (K − t) and the number of binary classifiers to be combined is
|A
t
| = (K − t)(K − t − 1)/2. This new elimination decoding is different of the Direct
Acyclic Graph [12] since at each iteration, all the outputs of candidate binary classifiers
are combined to determine the class to be eliminated. Whereas with a DAG, only one
classifier output is used for eliminating a class at each iteration.
3.3 Staking Decoding
The combination of the class membership estimates can be performed via a separate
trainable classifier [23, 28]. This classifier is seen as a Meta Classifier fed by the out-
put vector f (x) of all the binary classifiers. This method is also referred to as stacking
[29]. This approach seems more suitable than all the previous ones for the following
reason. As said before, combining classifiers which have never seen instances from
one same class during the training phase results in combining different information
sources. The combination of these ignorant classifiers (a binary classifier has seen only
two classes among K) with respect to the others can therefore result in almost ran-
dom classification. Indeed decoding methods such as voting rely on the assumption that
the relevant classifiers mainly predict the correct class and provide more votes to the
true class than the irrelevant classifiers to any other class. However if some of the rele-
vant classifiers predict wrong classes, the final classification can be also wrong. Since
we cannot predict the behavior of irrelevant classifiers, more sophisticated decoding
schemes are needed. To that aim, a trainable classifier is used with as training input the
output vector f(x) of all the binary classifiers. Each feature vector x
i
, (i = 1, .., N)
57

of the training set D
T rain
is used to feed all the binary classifiers. A new example
(f(x
i
), y
i
)) is then obtained. Such a process can be repeated so that a new training
set D
′
T rain
= {(f(x
1
), y
1
), ..., (f(x
N
), y
N
)} is generated. The new training data set is
used to train a Meta Classifier which predicts the final class by F (x) = h(g(f(x))). The
function h ◦ g designs the Meta Classifier to be used. The D
′
T rain
database generated
by all the binary classifiers provides valuable information about the possible mislead-
ing predictions caused by the irrelevant classifiers. The potential gain of stacking for
decoding is evident and it can lead to correct predictions where other methods would
fail [28, 30].
4 Experimental results
This section presents an experimental comparison of the ways to combine binary neural
networks according to the different combining rules. The databases for which results
will be presented here are data bases coming from the Machine Learning Data Repos-
itory of the University of California at Irvine (UCI) [31]. Table 1 describes the dif-
ferent databases showing the variety of training data set sizes (|D
T rain
|), the number
of classes (K), the number of neural networks (B) and the dimensionality of the data
input (|x|). The tests are performed on a data set (D
T est
) independent of the training
set. Table 2 presents all the classification rates obtained on D
T est
for the different
Table 1. Data bases used for the tests.
Database K |D
T rain
| |D
T est
| |x| B
Iris 3 120 30 4 3
Wine 3 144 34 13 3
Vehicle 4 679 167 18 6
PageBlocks 5 4382 1091 10 10
SatImage 6 4435 2000 36 15
Shuttle 7 43500 14500 9 21
PenDigits 10 7494 3498 16 45
OptDigits 10 3065 760 64 45
Serous 18 3870 1967 46 153
Letter 26 16000 4000 16 325
combining rules (best rates bold faced for each decoding rule family). For the standard
decoding, the results are homogeneous, except for Hastie and Price methods which per-
form significantly worse on several datasets. As expected from the litterature, ECOC
decoding performs very well and provides results always better than the Majority Vote.
One thing to point out with ECOC is that it can be a robust combining method as long
as the errors of the binary classifiers are not correlated [13, 15]. For this purpose all
the dichotomies must be as dictinct as possible, using well-tuned binary classifiers does
the matter and explains why ECOC works well in our study. When ECOC is not best
combining method, best results are obtained with the proposed Min-Max method which
confirms the intuitive idea that in some cases the irrelevant classifiers have strong influ-
ence on the final decision. Another advantage of the Min-Max method is its simplicity.
58
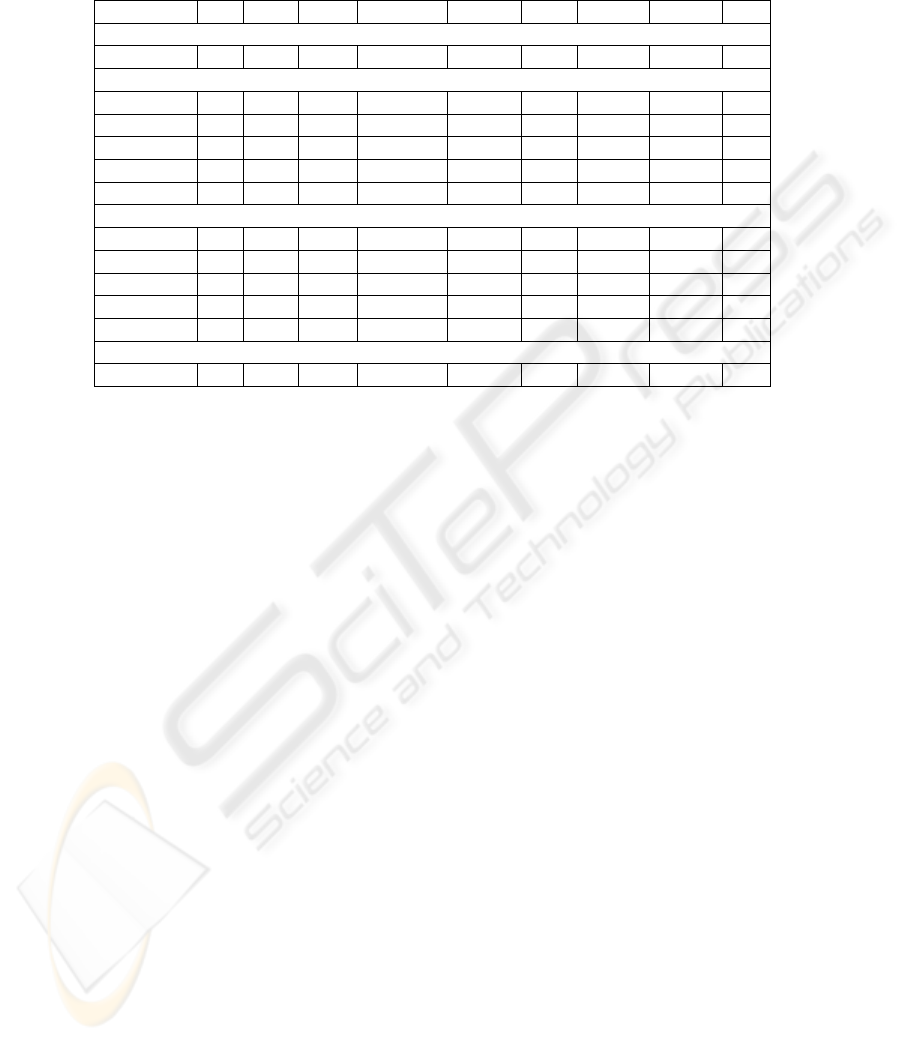
Table 2. Classification rates of the different decoding methods.
Iris Wine Vehicle PageBlocks SatImage Shuttle Pendigits Optdigits Letter
all-at-once
MLP 70.00 97.06 66.67 84.80 80.00 79.15 83.82 90.39 62.45
one-against-one standard decoding
Majority vote 70.00 97.06 69.46 88.27 77.90 95.70 89.17 91.70 78.37
Hastie 63.33 97.06 68.26 42.35 80.10 95.01 82.19 81.69 65.50
Price 63.33 97.06 70.06 46.29 79.90 95.18 88.42 87.62 71.57
Ecoc 70.00 97.06 69.46 88.45 80.10 95.82 89.05 90.91 78.52
Min-Max 70.00 97.06 69.46 88.36 78.35 95.57 89.22 91.83 77.72
one-against-one elimination decoding
Majority vote 70.00 97.06 68.26 88.36 77.85 95.66 89.19 91.04 78.44
Hastie 70.00 97.06 68.86 88.36 78.20 95.63 89.14 91.17 77.54
Price 70.00 97.06 68.86 88.45 78.10 95.62 89.11 91.17 77.64
Ecoc 70.00 97.06 68.86 88.45 78.20 95.76 89.17 91.17 78.47
Max-Min 70.00 97.06 69.46 88.36 78.35 95.59 89.28 91.70 77.67
Stacking decoding
C4.5 90.00 100.00 75.40 92.30 85.10 99.80 93.10 93.02 81.00
One can therefore say that even if the results are very mixed, two standard decoding
schemes can be retained as the best ones : ECOC and the proposed Min-Max method.
If we have a look now to the results obtained with the proposed elimination decod-
ing method, the first interesting thing is that the results look much more homogeneous
between the different combining rules. As it was noted by Platt with DAGs, using an
iterative elimination method reduces the error bound [12] since it avoids the problem
of irrelevant regions of classification. However the elimination method we propose per-
forms in general better than classical DAGs [14], proving that using an elimination
method based on combining rules is a more robust method than one based on a deci-
sion tree of binary classifiers, whitout the problem of optimizing the structure of the
tree. This is all the more interesting since our elimination decoding reduces the error
bound whatever the combining rule. As for the standard decoding method the two best
combining rules are ECOC and Max-Min (since we perform an elimination we do not
have Min-Max : at each iteration the class minimizing the highest pairwise probability
is eliminated). Finally we analyze the results of the proposed stacking decoding. First
of all one has to note that using a meta-classifier for stacking implies to cope with quite
large problems. For example for the 26-class Letter dataset, there are 26 × 25 = 650
predictions for each of 16000 examples. We have used decision trees (C4.5 [32]) meta-
classifiers to perform stacking. The stacking meta-classifier is fed with the input vector
f(x) of all the predictions provided by the binary classifiers. On all datasets a 10-fold
cross validation is performed. It can be seen that stacking decoding always give the best
results on all the datasets. For several of them very significant improvements over all
the other decoding methods are obtained. As compared to the work in Savicky [28], the
use of posterior probabilities instead of hard class decisions of the binary classifiers to
feed the stacking meta classifier enables substantial gain in the recognition rate. Simple
59

meta-classifier such as decision tree which are linear classifier are sufficient to obtain
better results than with a classical all-at-once MLP approach as seen in Table 2. Using
binary classifiers is therefore very interesting since it can be viewed as an ensemble
method which performs a simplification of the problem by decomposing it, the latter
results been easier to classify by stacking than the initial ones all-at-once.
5 Conclusion
In this paper we reviewed and evaluated classical methods for multiclass classification
based on binary neural networks according to the one-against-one formalism. We have
also introduced a new standard decoding method (Min-Max) and a new elimination
decoding which are both as suitable as the classical methods presented in the litterature
as proved by the experiments. We also evaluated a technique using stacking decoding
where the basic idea is to replace the combining and selection rules by a single meta-
classifier that combines all the predictions of the binary classifiers. The training set
of the meta-classifier consists of all the predictions of the binary classifiers for each
training sample. Using stacking decoding leads to substential gain in the recognition
rate. Future work will concern the use of the set of one-against-one classifiers as a new
input sample generator [30] to increase the size of the training dataset of the meta
classifier when the latter is unbalanced, preliminary results having also shown a new
gain in the recognition rate.
References
1. Furnkranz, J.: Round robin classification. Journal of Machine Learning Research 2 (2002)
721–747
2. Furnkranz, J.: Pairwise classification as an ensemble technique. In: European Conference
on Machine Learning (ECML). (2002) 97–110
3. Lezoray, O., Cardot, H.: A neural network architecture for data classification. International
Journal of Neural Systems 11 (2001) 33–42
4. Price, D., Knerr, S., Personnaz, L.: Pairwise neural network classifiers with propabilistic
outputs. In: Advances in Neural Information Processing Systems (NIPS). Volume 7., MIT
Press (1995) 1109–116
5. Kressel, U.: Pairwise classification and support vector machines. In: Advances in Kernel
Methods, Support Vector Learning. MIT Press (1999)
6. Ou, G., Murphey, Y., Feldkamp, A.: Multiclass pattern classification using neural networks.
In: International Conference on Pattern Recognition (ICPR). Volume 4. (2004) 585– 588
7. Rifkin, R., Klautau, A.: In defense of one-vs-all classi.cation. Journal of Machine Learning
Research 5 (2004) 101–141
8. Hastie, T., Tibshirani, R.: Classification by pairwise coupling. The annals of Statistics 26
(1998) 451–471
9. Tax, D., Duin, R.: Using two-class classifiers for multiclass classification. In: International
Conference on Pattern Recognition (ICPR). Volume 2. (2002) 124–127
10. Lezoray, O., Fournier, D., Cardot, H.: Neural network induction graph for pattern recogni-
tion. Neurocomputing (2004) 257–274
11. Allwein, E., Schapire, R., Singer, Y.: Reducing multiclass to binary: a unifying approach for
margin classifiers. Journal of Machine Learning Research 1 (2000) 113–141
60

12. Platt, J., Cristianini, N., Shawe-Taylor, J.: Large margin dags for multiclass classification. In:
Advances in Neural Information Processing Systems (NIPS). Volume 12., MIT Press (2000)
547–553
13. Moreira, M., Mayoraz, E.: Improved pairwise coupling classification with correcting clas-
sifiers. In: European Conference on Machine Learning (ECML), Springer-Verlag (1998)
160–171
14. Hsu, C.W., Lin, C.J.: A comparision of methods for multi-class support vector machines.
IEEE Transactions on Neural Networks 13 (2002) 415–425
15. Mayoraz, E., Alpaydin, E.: Support vector machines for multi-class classification. In: Inter-
national Work conference on Artificial Neural Networks. Volume 2. (1999) 833–842
16. F. Tahahashi, S.A.: Optimizing directed acyclic graph support vector machines. In: Artificial
Neural Networks in Pattern Recognition (ANNPR). (2003)
17. Lu, B.L., Ito, M.: Task decomposition and module combination based on class relations: A
modular neural network for pattern classification. IEEE Transaction on Neural Networks 10
(1999) 1244–1256
18. Cardot, H., Lezoray, O.: Graph of neural networks for pattern recognition. In: International
Conference on Pattern Recognition (ICPR). Volume 2. (2002) 124–127
19. Campbell, C.: Constructive Learning Techniques for Designing Neural Network Systems.
San Diego: Academic Press (1997)
20. Kwok, T.Y., Yeung, D.Y.: Constructive algorithms for structure learning in feedforward
neural networks for regression problems. IEEE Trans. on Neural Networks 8 (1997) 630–
645
21. Friedman, J.: Another approach to polychotomous classification. Technical report, Dept. of
statistics, Stanford University (1996)
22. Crammer, K., Singer, Y.: On the learnability and design of output codes for multiclass prob-
lems. Machine Learning 47 (2002) 201 – 233
23. Klautau, A., Jevti
´
c, N., Orlitsky, A.: Combined binary classifiers with applications to speech
recognition. In: International Conference on Spoken Language Processing (ICSLP). (2002)
2469–2472
24. Klautau, A., Jevti
´
c, N., Orlitsky, A.: On nearest neighbor error-correcting output codes with
application to all-pairs multiclass support vector machnies. Journal of Machine Learning
Research 4 (2003) 1–15
25. Ko, J., Kim, E., Byun, H.: Improved n-division output coding for multiclass learning prob-
lems. In: International Conference on Pattern Recognition (ICPR). Volume 3. (2004) 470–
473
26. Phetkaew, T., Kijsirikul, B., Rivepiboon, W.: Reordering adaptive directed acyclic graphs:
an improved algorithm for multiclass support vector machines. In: International Joint Con-
ference on Neural Networks (IJCNN). Volume 2. (2003) 1605– 1610
27. Vural, V., Dy, J.G.: A hierarchical method for multi-class support vector machines. In:
International Conference on Machine Learning (ICML). (2004)
28. Savicky, P., Furnkranz, J.: Combining pairwise classifiers with stacking. In: Intellignent
Data Analysis (IDA). (2003)
29. Wolpert, D.: Stacked generalization. ’Neural Networks 5 (1992) 241–260
30. Zhou, Z.H.: Nec4.5: Neural ensemble based c4.5. IEEE Transactions on Knowledge and
Data Engineering (2003)
31. S. Hettich, C.B., Merz, C.: UCI repository of machine learning databases. Technical report,
University of California, Irvine, Dept. of Information and Computer Sciences (1998)
32. Quinlan, J.: C4.5 : programs for machine learning. Morgann Kauffman, San Mateo (1993)
61
