
Efficient Gridding
of Real Microarray Images
2
Giuseppe Lipori
1
1
Dipartimento di Scienze dell’Informazione
Universit
`
a degli Studi di Milano
Via Comelico, 39/41 - 20135 Milano
2
Work partially supported by the PASCAL Network of Excellence under EC grant no. 506778.
Abstract. DNA microarrays technology is very recent and rapidly evolving. At
present, it is widely used in the analysis of gene expression. The interpretation of
the data crucially depends on the accuracy of the localization of the circular spots,
which are placed in rectangular grids. The problem is complicated by the presence
of many local deformations of the grid, by the high variability in luminance of
the spots, by noise and other disturbances due to the biological nature of the
experiments. In this paper we implement an automatic method for the gridding of
real microarrays that takes into account most of the open problems by exploiting a
recently introduced image transform, the Orientation Matching Transform, which
enhances circular patterns of a specific size.
1 Introduction
DNA microarray consists of a solid surface onto which DNA molecules have been
chemically bonded. Microarrays are widely used to study gene expression in order to
associate gene activities with biological processes and to group genes into networks of
interconnected activities. They are very advantageous since they allow to measure the
expression of thousands of genes in parallel and in a quasi automated way. On the other
hand every microarray experiment poses the problem to handle and analyze a huge mass
of data, which is often corrupted by noise or some other disturbances.
A common type of microarray is called pin spotted because it is produced via a
robotic arm that spots the DNA probes on the microscope slides. The robot is shaped as
a grid of pins and so a typical spotted microarray is composed of a set of regular grids of
circular spots, as schematized in Figure 1. This is the type of microarrays on which we
will focus and when we speak of microarrays we really intend pin spotted microarrays.
For a full explanation of how microarrays are engineered and for a survey of all types
of existing technologies refer to [11].
The result of a microarray experiment is presented in the form of an image, where
the most expressed genes are indicated by high intensity spots. The first stage of the
analysis is called gridding, that is the process of assigning coordinates to the spot lo-
cations. Then the data is segmented in order to separate the foreground pixels from
the background. Finally comes the intensity extraction that corresponds to reading the
intensity of expression of each spot.
Lipori G. (2005).
Efficient Gridding of Real Microarray Images.
In Proceedings of the 1st International Workshop on Biosignal Processing and Classification, pages 121-130
DOI: 10.5220/0001192501210130
Copyright
c
SciTePress
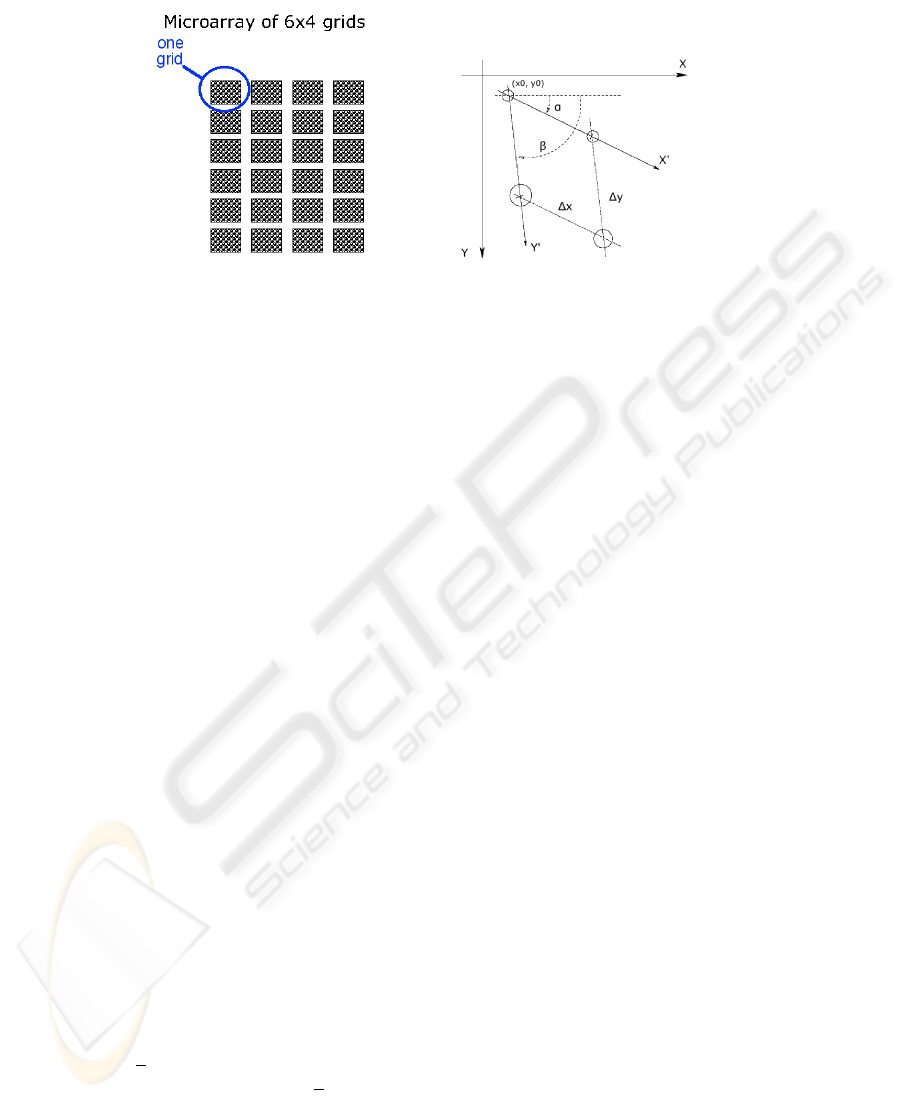
Fig.1. The structure of a microarray and the image axes vs. the grid axes.
We will limit the analysis to the gridding, which is a crucial phase as the accuracy of
the whole analysis depends on the precision with which spots are located. Sometimes
the problem of gridding is solved by requiring human intervention to specify some
points in the grid or even to register individual spots. This article aims at automatizing
the gridding task as much as possible via the application of a deformable gridding
proposed in [2] and then developed in [3], [4]. The method is based on the Orientation
Matching Transform (OMT) presented in [5] and until now it has been evaluated solely
on synthetic images generated for the purpose. The contribution of this paper is the
adaptation of the technique to make it suitable and robust for the treatment of real
images of microarrays that present much more difficulty to the gridding.
2 Gridding
Both the number of grids on a slide and the number of spots within a grid may vary
in different microarrays. In general the space between the grids is much larger than the
space between the spots and this suggests to treat each grid separately. An example of
a good quality microarray grid is shown in Figure 2.
The biological nature of the data makes it prone to a number of problematic situa-
tions that make gridding a difficult task: high background noise, irregular shape or size
of the spots, presence of faint spots, imperfect alignment of the spots along the rows
or columns of the grid, local deformations as well as small rotations of the grid due to
wrong placement under the image scanner, sensible skew of the two axes and so on. All
these issues need to be treated automatically in order to locate the spots in an accurate
way. However most of the approaches so far presented for microarray gridding, e.g. [1]
and [8], try to pose some restrictions on the data or make strong assumptions, such as
requiring grid rows and columns perfectly aligned along the x and y axes of the image.
In our approach we assume the axes of the grid free to rotate with respect to the
axes of the image (see Figure 1). In particular the row axis X
′
can make an angle
α <
π
2
with the horizontal axis X of the image, and the column axis Y
′
can make
with X
′
an angle β − α 6=
π
2
. Moreover, we will allow the spacings (∆x, ∆y) of the
122

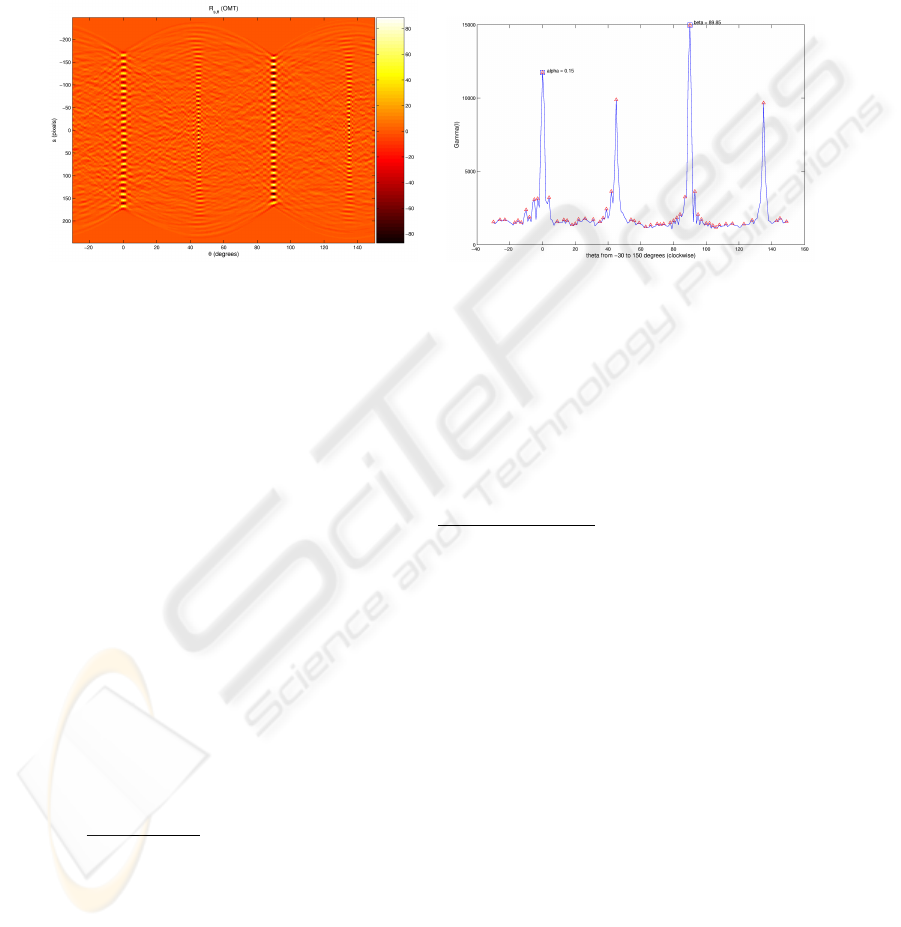
Fig.2. A good quality grid and its OMT (with parameters r = 2, R = 4)
spots (along the columns and the rows respectively) to be different, and we assume no
a priori knowledge on the number of rows and columns.
The strategy of the gridding is divided into the following, successive steps:
– OMT: transform of the image to enhance the circular objects of a specified size;
– regular grid: use of the Radon Transform (RT) to project the OMT output along
all directions in order to identify the axes’ angles α and β; the knowledge on an-
gles enables us to determine the grid spacings and the coordinates of the first spot
(x
0
, y
0
); the tuple (α, β, ∆x, ∆y, x
0
, y
0
) completely specifies the regular grid po-
sitions (x
ij
, y
ij
)
x
ij
= x
0
+ i∆y cos β + j∆x cos α
y
ij
= y
0
+ i∆y sin β + j∆x sin α (1)
that best match the actual microarray grid;
– deformable grid: deformation of the regular grid by adopting a Bayesian approach:
choice of the trade off between regularity and accuracy of superposition on the
actual spots, calculated via a Maximum A Posteriori (MAP) scheme.
2.1 Orientation Matching Transform
The OMT is an extension of the Hough Transform for circles and was first proposed
in [5]. Our scope here is to accurately segment the spots from the background. Two
common approaches to the problem would be to work on the edge image or to threshold
the gray scale image according to some criteria. Both these strategies suffer from many
complications due to the high variability of spot luminance, to the presence of noise and
in particular to the existence of many spots that are almost as dark as the background.
The OMT presents the sure advantage that it does not work on the absolute luminance
of the spots and it is essentially invariant to contrast changes.
In details, let A
R
r
(0, 0) be the annulus of radii r and R centered in the origin, that is
A
R
r
(0, 0) =
(x, y) ∈ R | r ≤ x
2
+ y
2
≤ R
.
123

If we define φ
∗
in such a way that
cos φ
∗
(x, y) =
x
p
x
2
+ y
2
; sin φ
∗
(x, y) =
y
p
x
2
+ y
2
.
and if φ(x, y) is the orientation of the image gradient in (x, y), then the OMT is given
by
3
:
OM(u, v) =
1
π(R
2
− r
2
)
×
ZZ
A
R
r
(u,v)
cos (φ
∗
(x − u, y − v) − φ(x, y)) dx dy (2)
The factor
1
π (R
2
−r
2
)
is equal to the inverse of the area of the annulus A
R
r
(u, v); it works
as a normalization factor to obtain −1 ≤ OM (u, v) ≤ 1. In words, (2) uses the cosine
to measure the similarity between the orientation φ
∗
of the gradient of ideal circles
centered in (u, v) (with radii ranging in [r,R]) and the orientation of the image gradient
around the same point. It is sufficient to know the range of radii of the spots in a certain
microarray to apply the correct transform
4
.
Figure 2 shows the output of the OMT for the sample image; notice how the faint
spots are partially recovered in the transform image.
Since cos(φ
∗
− φ) = sin φ
∗
sin φ + cos φ
∗
cos φ, the OMT can be implemented
as the sum of two image filterings, which is computationally much more efficient than
applying the definition as it is.
2.2 Radon Transform projections
The Radon Transform [9] is at the basis of Computer Tomography because it permits
to reconstruct an unknown 2-dimensional function (typically the image of a slice of
biological tissue) by calculating its integral along all lines passing through it in all
possible directions. In our context we do not need the inverse transform, what we need
is to identify the direction of the axes X
′
and Y
′
of the grid. We do it by analyzing the
projections of the OMT image over different orientations.
The formal definition of the 2D RT of a signal f is
R
s,φ
(f) =
Z
∞
−∞
Z
∞
−∞
f(x, y)δ(x cos φ + y sin φ − s) dx dy (3)
where the Kronecker delta is used to specify the line of integration defined in polar
coordinates (s, φ).
3
Our definition is equivalent to the original
O M (u, v) =
1
2π(R − r)
×
A
R
r
(u,v)
cos (φ
∗
(x − u, y − v) − φ(x, y))
(x − u)
2
+ (y − v
2
)
dx dy
as both exhibit the desired property of normalization (they are both dimensionless).
4
Usually the right parameters r and R remain fairly constant across experiments made on the
same type of support. However they can vary very much from microarray to microarray and it
is crucial to choose a good couple of radii for the gridding to work.
124
If I is the gray scale image of the grid, we are interested in the function
5
Γ
φ
(I) =
Z
s
|R
s,φ
(OM(I))| ds (4)
Fig.3. The Radon transform vs. the Γ
φ
peaks
The left side of Figure 3 depicts the output of R
s,φ
(OM(I)) applied to the image in
Figure 2; notice how the projection width shrinks and how the profile gets better defined
as the angle approaches the perfect alignment with an axis of the grid. On the right side
it is shown the behavior of Γ
φ
(I); the main directions of the grid are calculated by
choosing the two peaks that are best correlated according to the criterium
(α, β) = arg max
(φ
1
,φ
2
)
Γ
φ
1
(I) · Γ
φ
2
(I)
1 + | cos(φ
1
− φ
2
)|
The two sub-peaks corresponding to the diagonals of the grid are also visible.
The identification of α and β allows us to study the row and column structure of
the grid. In principle it would be enough to take R
s,α
(OM(I)) and R
s,β
(OM(I)) over
all s, and to study the two profiles separately in order to estimate the number of rows
and columns and the respective spacings (∆
x
, ∆
y
). However care must be taken at this
stage of the gridding because the shape of the two projections can pose some problems:
there can be very different peak intensities due to rows/columns with many faint spots
and, above all, false peaks can be caused by dirt found on the slide in between the wells
that contain the spots. Therefore there is need for some processing to normalize the
signals and clean them from possible causes of error.
5
Differently from [3], in (4) we introduce the absolute value because the integral of
R
s,φ
(OM (I)) over s is equal along all directions and it is close to zero (recall −1 ≤
O M (u, v) ≤ 1), while the integral of |R
s,φ
(OM (I))| increases with the accentuation of
peaks (w.r.t. valleys) in the projection.
125
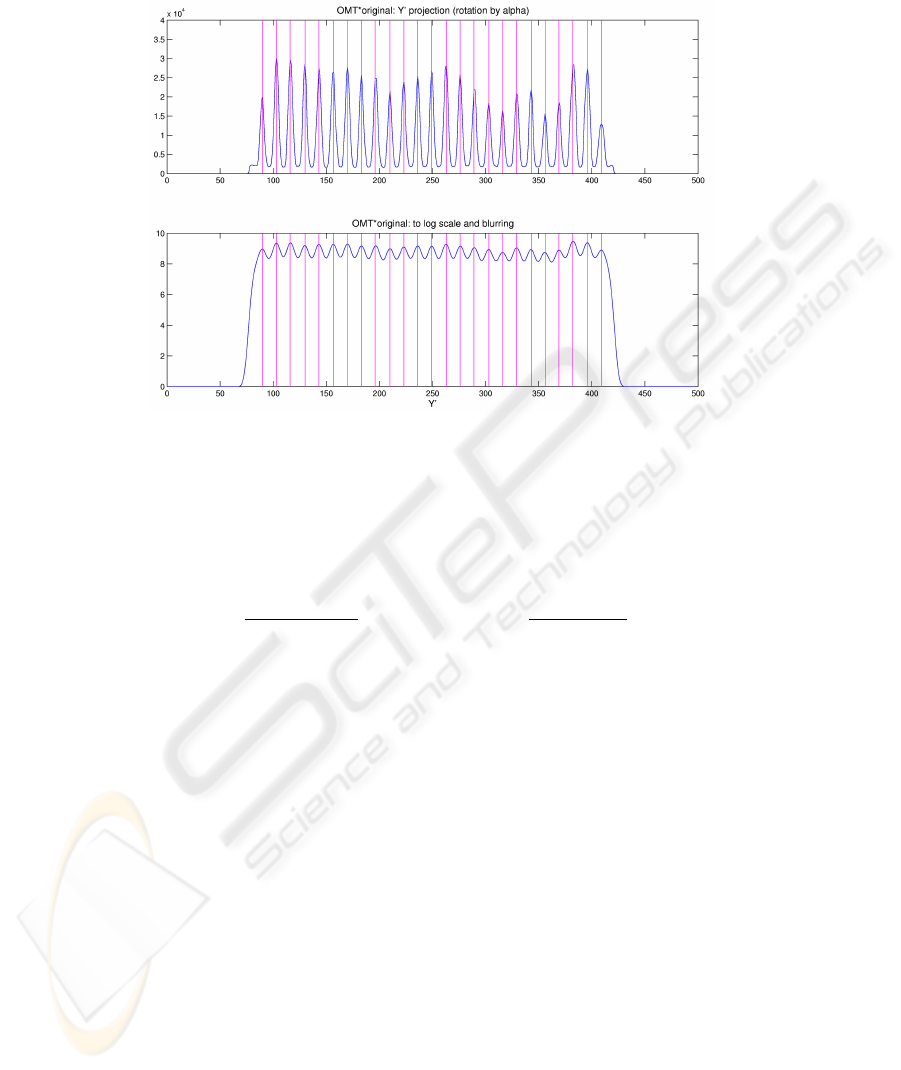
Fig.4. The Y
′
profile corresponding to the projection of the grid transform along angle β (before
and after treatment)
To this end, we experimentally found that it is much more robust to analyze the
profile of a reinforcement of the OMT, that is to use the projections of
R
s,φ
(1 + OM (I))
2
· I
, where 0 ≤
1 + OM (I)
2
≤ 1 .
Afterwards we attenuate the variability in peak intensities by passing to the loga-
rithmic scale and, in order to flatten the false peaks, we apply a Gaussian filtering whose
support size depends on a rough estimate of the peak spacing. See Figure 4 for the Y
′
axis projection (before and after treatment) of the sample image (the X
′
axis projection
is analogous).
After the individuation of all peaks we use (1) to build the regular grid (Figure 5)
that best overlaps the microarray grid.
2.3 Bayesian gridding
The final step of the gridding technique aims at deforming the regular grid in order to
get the best possible match between the spot centers and the grid positions. A possible
solution to this problem is to use a Bayesian scheme of inference, like that proposed in
[7]. This methodology consists in building a model of microarray grids (the so called
prior) and use a Maximum A Posteriori (MAP) approach to establish which is the best
gridding on a given instance of the problem according to that model. In symbols, if I is
the image in input to our system and G is the model of the grid, we want to find G that
126

maximizes
P (G|I) =
P (G)P (I|G)
P (I)
∝ P (G)P (I|G) (5)
The choice of the grid model is very important because on one hand its precision im-
proves the quality of the gridding, but on the other hand its richness in details affects
the complexity of the computation of
G
∗
= arg max
G
P (G)P (I|G) = arg max
G
log P (G|I) . (6)
In [7] the model G really describes a grid because it takes into account both the posi-
tions of the spots and the length of the arcs that connect each spot to its neighbors. For
simplicity we follow the analysis of [4], where G is in fact a prior based on 1-cliques:
each spot is treated independently of its neighbors and of the rest of the grid. However,
while they use a computationally expensive and potentially sub-optimal algorithm (the
Simulated Annealing) to solve (6), we exploit the mutual independence of the spots
to find the optimal solution in an efficient fashion. If a grid is just a collection of in-
dependent spots, then every spot g
ij
is assumed identically distributed (according to a
Gaussian distribution) around the corresponding position t
ij
of the regular grid. The
joint distribution of G becomes very simple
P (G) ∝ exp
−
1
2
X
ij
(g
ij
− t
i,j
)
T
Σ
−1
ij
(g
ij
− t
i,j
)
The model of G depends only on the variance of the Gaussian distribution, which should
be estimated from a sample of grids. However we assume no mutual dependence of the
Gaussian displacements along the two axes (zero covariance) and we fix
Σ
ij
= Σ =
σ
2
g
x
σ
g
x
· σ
g
y
σ
g
y
· σ
g
x
σ
2
g
y
=
∆x
k
0
0
∆y
k
where k is a constant that regulates the amplitude of the spots’ displacement.
The second factor of the objective function is the likelihood that measures how well
the observed instance fits the model. Like in [4] we adopt as observation model
P (I|G) ∝ exp
−
1
2
X
ij
(1 − OM (g
ij
))
2
that is we estimate the accordance of the model with the observed data by measuring
how close the locations of the deformable grid are to the center of circular objects. It is
clear that the deformation of the regular grid is performed by varying the model G in
order to find
G
∗
= arg max
G
log P (G|I) = arg max
G
{log P (I|G) + log P (G)} (7)
by balancing the opposite contributions of the first term, which privileges the regularity
of the grid, and the second one, which rewards a good matching of the grid with the real
spots’ positions.
127

It is important to notice that the objective function (7) can be decomposed in a set
of independent sub-problems, each corresponding to a single spot
g
∗
ij
= arg min
g
ij
(g
ij
− t
i,j
)
T
Σ
−1
ij
(g
ij
− t
i,j
) + (1 − OM (g
ij
))
2
and G
∗
can be calculated quite efficiently by an exhaustive visit of a small neighborhood
of each t
ij
without implementing a more sophisticated search algorithm. The process
produces the result shown on the right in Figure 5.
Fig.5. The regular grid vs. the deformed grid
3 Experimental results
The experimental evaluation of our gridding technique has been quite difficult to ac-
complish because of the lack of ground truth available on real biological data. However
we wanted to avoid the generation of artificial microarray grids to test upon, since the
synthetic images do not simulate very effectively all the involved variables: variability
of the spots’ shape, the “texture” of the background and its noise, the presence of imper-
fections due to the unskillfulness of the experimenter and so on. It is sufficient to take a
look at the internet site of the Stanford Microarray Database (SMD) [10] to realize how
heterogeneous microarrays are; this is the consequence of the variety of supports avail-
able combined with the unequal experience of different experimenters, plus the fact that
a single experiment is so expensive that it might not be convenient to repeat it in case
of imperfections.
As a term of comparison we use the gridding done by the software GenePix [6],
which is a sophisticated commercial software very popular among bioinformaticians
6
.
6
GenePix carries out the complete analysis of a microarray plate, from the gridding to the inten-
sity extraction. Unfortunately its specifications do not give any information on the principles
of its functioning, nor on its computational cost, being it a proprietary software.
128
The SMD makes available many GenePix raw data output files, which contain the coor-
dinates of the bounding box of each spot, together with the original microarray images.
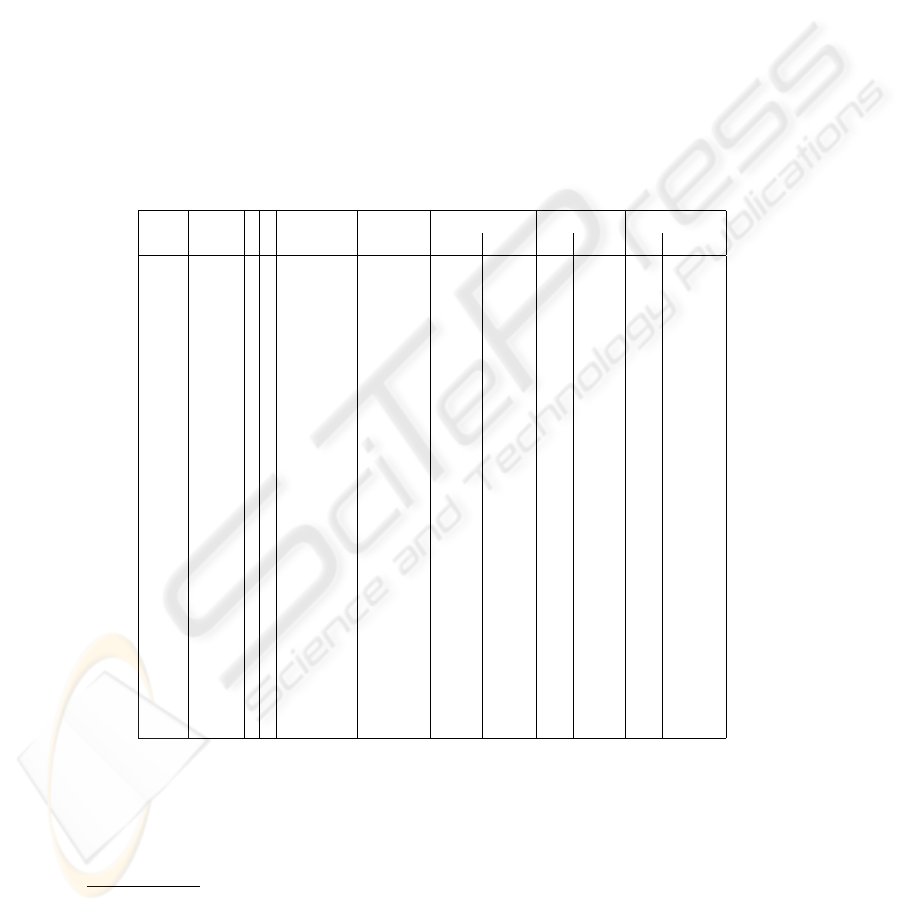
In Table 1 we present the evaluation of our gridding technique given in terms of statis-
tics on the distance between the locations of the deformed grid and the centers of the
bounding boxes, taken as the ground truth of the data. The choice of parameters (r, R)
for each microarray is made by presenting to a human operator the output of the OMT
on a grid chosen at random and over a wide range of possibilities (R ∈ {4, . . . , 10}
and r ∈ {R − 4, . . . , R − 1}), asking for a preference. The best possible choice that
can be made visually is the one that produces the OMT with the brightest and sharpest
peaks in correspondence to the spot locations. The difference R − r decreases with the
regularity of the spots’ size within the grid and, in ideal conditions, the choice should
be such that r = R − 1.
Table 1. Gridding results
ID grids r R grids time per mean angles error: mean error: std dev
size completed grid (sec) α β x y x y
11704 26×26 4 6 11/32 15.8 -0.32
◦
90.43
◦
1.09 1.05 0.87 0.94
14013 31×32 4 5 32/32 19.7 0.02
◦
89.94
◦
0.59 0.60 0.22 0.31
14317 26×26 3 6 3/32 15.5 -0.4
◦
90.1
◦
0.88 0.98 0.72 0.93
15989 18×19 6 8 16/16 13.2 0.59
◦
90.02
◦
0.83 1.12 0.60 1.28
17995 19×19 4 7 16/16 14.8 -0.12
◦
89.89
◦
1.01 1.18 0.80 0.97
19880 20×20 6 7 5/16 15.5 0.68
◦
89.91
◦
1.36 1.67 1.17 1.69
20385 18×18 7 8 36/48 13.3 0.14
◦
91.44
◦
3.98 7.73 6.70 9.48
21635 13×16 6 7 44/48 9.5 -0.51
◦
89.63
◦
1.26 2.44 2.25 3.62
22588 18×16 6 8 9/16 10.1 8.15
◦
98.42
◦
1.13 1.46 0.95 1.53
24047 19×19 7 8 15/16 14.3 0.16
◦
90.08
◦
0.91 1.03 0.89 1.02
24494 17×17 3 6 13/16 11.6 -1.11
◦
89.78
◦
1.28 1.63 1.02 1.83
24753 15×16 3 4 11/32 8.7 0.39
◦
90.1
◦
3.88 1.70 2.86 1.56
25978 30×30 5 6 48/48 19.7 0.20
◦
90.22
◦
0.68 1.05 0.59 0.82
30855 18×18 7 8 16/16 13.0 0.1
◦
89.93
◦
0.82 0.85 0.76 0.71
31784 18×20 5 7 14/32 12.6 -0.09
◦
89.96
◦
1.86 3.45 4.72 6.98
32827 17×17 3 5 16/16 11.4 0.44
◦
90.37
◦
0.89 1.23 0.81 1.04
32898 30×30 4 5 43/48 21.8 -0.1
◦
89.95
◦
0.77 1.57 0.68 1.32
34727 24×24 4 5 4/16 16.0 0.77
◦
90.22
◦
0.99 1.21 0.90 1.15
40380 18×20 5 7 31/32 12.6 0.65
◦
89.63
◦
1.11 1.00 0.91 0.83
4047 22×24 4 5 7/16 14.4 -0.35
◦
89.89
◦
0.92 1.33 0.67 1.53
42420 25×26 5 6 15/16 16.8 -0.17
◦
89.88
◦
2.73 1.68 6.21 1.38
51736 22×22 5 7 48/48 16.3 -0.10
◦
89.89
◦
0.66 1.06 0.61 0.84
Table 1 also reports the experiment ID of each microarray in the SMD and the
average execution time.
7
7
Implementation in MATLAB on a Pentium 4 (3.2 GHz) machine.
129

4 Discussion and conclusion
Our method automatically detects failure of the gridding, which is often due to inputs
whose structure does not match the expected logical structure of Figure 1. For instance
there are frequent situations
8
in which a correct gridding can never be obtained with
our technique because one or more rows are systematically missing at the bottom of
the grids (due to irrelevant expression of the corresponding genes), so preventing any
possible solution solely based on the data. This is a problem specific to the context of
microarrays that is not sufficiently taken into account by the general method.
In the remaining cases
9
the gridding works very well as both the error mean and
standard deviation often kept around one pixel, which is desirable and comparable to
the results achieved in [4] over synthetic images
10
.
In our experience, the prominent cause of failure is the incorrect evaluation of the
number and position of rows/columns, which results in the automatic discard of the
gridding. Probably it would be enough to require human intervention for the introduc-
tion of the correct number of rows/columns
11
to achieve a much better performance on
most experiments. In our future work we intend to examine this variant.
References
1. J Angulo and J Serra. Automatic Analysis of DNA Microarray Images using Mathematical
Morphology. Bioinformatics, 19(5):553–562, 2003.
2. G Antoniol and M Ceccarelli. A Markov Random Field Approach to Microarray Image
Gridding. Proceedings of the IEEE International Conference on Pattern Recognition, 2004.
3. G Antoniol, M Ceccarelli, and A Petrosino. Microarray Image Addressing Based on the
Radon Transform. Proceedings of the IEEE International Conference on Image Processing,
2005.
4. M Ceccarelli and G Antoniol. A Deformable Grid Matching Approach for Microarray Im-
ages. Technical report at the Research Center on Software Technologies (RCOST), 2005.
5. M Ceccarelli and A Petrosino. The Orientation Matching Transform Approach to Circu-
lar Object Detection. Proceedings of IEEE International Conference on Image Processing,
pages 712–715, 2001.
6. GenePix Pro. Software for Microarray Image Analysis by Axon Instruments. Web address:
http://www.axon.com/GN
GenePixSoftware.html.
7. K Hartelius, J M Cartensen, A Snijders, R Segraves, D Albertso, and D Pinkel. Bayesian
Grid Matching. IEEE Transactions on PAMI, 2(25):162–173, 2003.
8. A N Jain, T Tokuyasu, A Snijders, R Segraves, D Albertso, and D Pinkel. Fully Automatic
Quantification of Microarray Image Data. Genome Research, 12:325–332, 2003.
9. A G Ramm and A I Katsevich. The Radon Transform and Local Tomography. CRC Press,
1996.
10. Stanford Microarray Database. Public directory of Microrray Experiment Data. Web ad-
dress: http://genome-www5.stanford.edu/.
11. Dov Stekel. Microarray Bioinformatics. Cambridge University Press, Cambridge, UK, 2003.
8
Experiments 11704, 14317, 19880, 20385, 21635, 22588, 24047, 34727, 4047.
9
Experiments 14013, 15989, 17995, 25978, 30855, 32827, 51736, 24047, 32898, 40380.
10
The authors report a Mean Square Error varying from 1 to 4 pixels, depending on the noise
variance chosen in the construction of the artificial grids (from 0 to 10 pixels).
11
This would require just one intervention per microarray, being all its grids of the same size.
130
