INCREMENTAL LEARNING IN HIERARCHICAL NEURAL

NETWORKS FOR OBJECT RECOGNITION

Rebecca Fay, Friedhelm Schwenker and G

unther Palm

University of Ulm

Department of Neural Information Processing

D-89069 Ulm, Germany

Keywords:

Object recognition, hierarchical neural networks, incremental learning.

Abstract:

Robots that perform non-trivial tasks in real-world environments are likely to encounter objects they have not

seen before. Thus the ability to learn new objects is an essential skill for advanced mobile service robots. The

model presented in this paper has the ability to learn new objects it is shown during run time. This improves

the adaptability of the approach and thus enables the robot to adjust to new situations. The intention is to verify

whether and how well hierarchical neural networks are suited for this purpose. The experiments conducted

to answer this question showed that the proposed incremental learning approach is applicable for hierarchical

neural networks and provides satisfactory classiﬁcation results.

1 INTRODUCTION

When performing tasks in complex environments it

is probable that a robot is confronted with objects it

has not seen before and consequently cannot identify.

This makes the ability to learn new objects during run

time an important capability for advanced mobile ser-

vice robots. The robot is then able to incrementally

learn novel objects and thereby increase knowledge

of its environment and adapt to new situations.

Without the ability to incrementally learn new ob-

jects the robot could only deal with predetermined ob-

jects learnt ofﬂine. All other objects could only be

classiﬁed as unknown objects. In real world environ-

ments which are fairly complex and subject to numer-

ous changes solely being capable of coping with pre-

viously learnt objects might not be sufﬁcient.

The presented approach is an extension of our pre-

vious work (Knoblauch et al., 2004) which enables

the model to deal with unknown objects by incremen-

tally learning to categorise these objects.

2 HIERARCHICAL OBJECT

RECOGNITION

The visual object recognition is implemented as a two

stage process (Fay et al., 2004) where low resolu-

tion features such as colour and shape information are

used to localise objects of potential interest and en-

suing high resolution features such as edges, corners

or T-junctions are extracted to analyse the part of the

image containing the detected object in greater detail.

These features are used in a trained neural network

for object recognition. For the application at hand ori-

entation histograms (Freeman and Roth, 1995) (Cop-

pola et al., 1998) summing up all orientations (direc-

tions of edges represented by the gradient) within the

region of interest are used as features for the object

recognition.

2.1 Hierarchical Neural Networks

If neural networks are used for object recognition an

object is represented by a number of features, which

form a d dimensional feature vector x within the

feature space X ⊆ IR

. A classiﬁer therefore re-

alises a mapping from feature space X to a ﬁnite set

of classes C = {1, 2, ..., l}. A neural network is

trained to perform a classiﬁcation task using super-

vised learning algorithms. A set of training examples

S := {(x

, t

), µ = 1, ..., M} is presented to the

network. The training set consists of M feature vec-

tors x

∈ IR

each labelled with a class membership

∈ C. During the training phase the network pa-

rameters are adapted to approximate this mapping as

accurately as possible. In the classiﬁcation phase un-

298

Fay R., Schwenker F. and Palm G. (2005).

INCREMENTAL LEARNING IN HIERARCHICAL NEURAL NETWORKS FOR OBJECT RECOGNITION.

In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 298-303

DOI: 10.5220/0001182002980303

 SciTePress

labelled data x

∈ IR

are presented to the trained

network. The network output K(x

) = c ∈ C is in-

terpreted as an estimation of the class corresponding

to the input vector x.

The object classiﬁcation is performed by a hier-

archical neural network (Fay et al., 2004). It con-

sists of several simple neural networks that are com-

bined in a tree, i.e. the nodes within the hierarchy

represent individual neural classiﬁers. For the ap-

plication at hand RBF networks were used as neural

classiﬁers. The basic idea of hierarchical neural net-

works is the hierarchical decomposition of a complex

classiﬁcation problem into several less complex ones.

This yields hierarchical class grouping whereby the

decision process is split into multiple steps exploit-

ing rough to detailed classiﬁcation. The hierarchy

emerges from recursive partitioning of the original

set of classes C into several disjoint subsets C

un-

til subsets consisting of single classes result. C

the subset of classes to be classiﬁed by node i, where

i is a recursively composed index reﬂecting the path

from the root node to node i. The subset C

of node

i is decomposed into s

disjoint subsets C

i,j

, where

i,j

⊂ C

, C

= ∪

−1

j=0

i,j

and C

i,j

∩ C

i,k

= ∅.

The total set of classes C

= C is assigned to the

root node. Consequently nodes at higher levels of

the hierarchy typically classify between larger sub-

sets of classes whereas nodes at the lowest level dis-

criminate between single classes. This divide-and-

conquer strategy yields several simple classiﬁers, that

are more easily manageable than one extensive clas-

siﬁer. These simple classiﬁers can be amended much

more easily to the decomposed simple classiﬁcation

tasks than one classiﬁer could be adapted to the origi-

nal complex classiﬁcation task. Furthermore different

feature types X

are used within the hierarchy. For

each classiﬁcation task the feature type that allows for

the best discrimination is chosen. An example of such

a hierarchy is shown in ﬁgure 1. The feature types X

and X

used for node i and j can be identical, i.e.

both can use the same feature type.

2.2 Hierarchy Generation

The hierarchy is generated by unsupervised k-means

clustering. In order to decompose the set of classes

assigned to one node i into s

disjoint subsets a

k-means clustering is performed with all data points

∈ X

∈ C

} belonging to these classes. De-

pending on the distribution of the classes across the

k-means clusters s

disjoint subsets C

i,j

are formed.

One successor node j corresponds to each subset. For

each successor node j again a k-means clustering is

performed to further decompose the corresponding

subset C

i,j

. The k-means clustering is performed for

each feature type. The different clusterings are eval-

uated and the clusterings which group data according

to their class labels are preferred. Since the k-means

algorithm depends on the initialisation of the clusters,

k-means clustering is performed several times per fea-

ture type. In this study the number of k-means clus-

tering per feature type was 10.

The number of clusters k must be at least the num-

ber of successor nodes or the number of subsets s

respectively but can also exceed this number. If the

number of clusters is higher than the number of suc-

cessor nodes, several clusters are grouped together so

that the number of groups equals the number of suc-

cessor nodes. For reasons of simplicity in the fol-

lowing only the case where the number of clusters k

equals the number of successor nodes s is considered.

The valuation function prefers clusterings that group

data according to their class labels. Clusterings where

data are uniformly distributed across clusters notwith-

standing their class labels receive low ratings. Fur-

thermore clusterings are preferred which evenly di-

vide the classes. Thus the valuation function rewards

unambiguity regarding the class afﬁliation of the data

assigned to a prototype as well as uniform distribution

regarding the number of data points assigned to each

prototype.

To generate the hierarchy at ﬁrst the set of all

classes is assigned to the root node. Starting with a

clustering on the complete data set the set of classes is

divided into subsets. Each subset is assigned to a suc-

cessor node of the root node. Now the decomposition

of the subsets is continued until no further decompo-

sition is possible or until the decomposition does not

lead to a new division. An example of a classiﬁcation

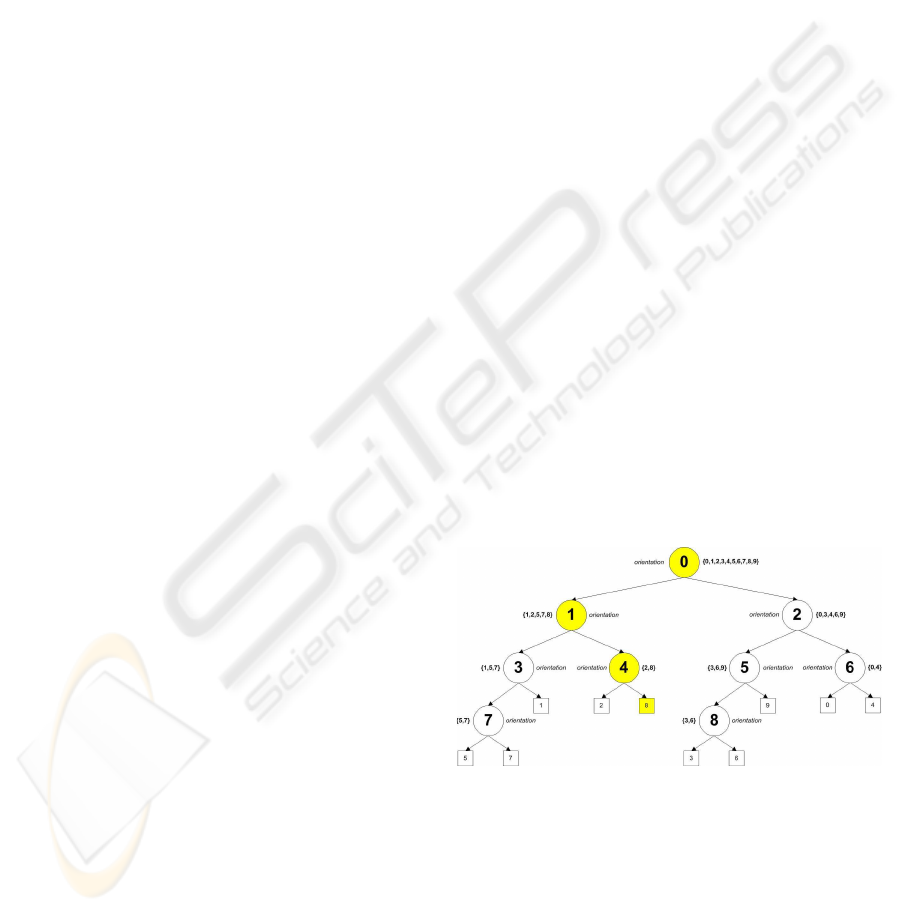
hierarchy is shown in ﬁgure 1.

Figure 1: Classiﬁer hierarchy generated for the classiﬁca-

tion of 10 classes of the COIL20 data set using orientation

histograms as feature type. Each node within the hierarchy

represents a neural network which is used as a classiﬁer.

The end nodes represent classes. To each node a feature

type and a set of classes is assigned. The corresponding

neural network uses the assigned feature type to discrim-

inate between the assigned classes. The highlighted path

shows the nodes activated during the classiﬁcation of a sam-

ple that is classiﬁed as class 8.

INCREMENTAL LEARNING IN HIERARCHICAL NEURAL NETWORKS FOR OBJECT RECOGNITION

299

2.3 Training and Classiﬁcation

The hierarchy is trained by separately training the in-

dividual classiﬁers with the data {x

∈ X

∈ C

}

that belong to the subsets of classes assigned to each

classiﬁer. For the training the respective feature type

identiﬁed during the hierarchy generation phase

is used. The data will be relabelled so that all data

points of the classes belonging to one subset C

i,j

have

the same label j, i.e.

= j, x

∈ X

, t

∈ C

i,j

The number of input nodes of the single classiﬁers is

deﬁned by the dimension d

of the respective feature

type X

assigned to the corresponding node i. The

number of output nodes equals the number of succes-

sor nodes s

. The classiﬁers are trained using super-

vised learning algorithms. The classiﬁers within the

hierarchy can be trained independently, i.e. all classi-

ﬁers can be trained in parallel.

Within the hierarchy different types of classiﬁers

can be used. Examples of classiﬁers would be radial

basis function (RBF) networks, linear vector quanti-

sation classiﬁers (Simon et al., 2002) or support vec-

tor machines (Schwenker, 2001). We chose RBF net-

works as classiﬁers. They were trained with a three

phase learning algorithm (Schwenker et al., 2001).

The classiﬁcation result is obtained similar to the

retrieval process in a decision tree (Duda et al., 2001).

Starting with the root node the respective feature vec-

tor of the object to be classiﬁed is presented to the

trained classiﬁer. By means of the classiﬁcation out-

put the next classiﬁer to categorise the data point is

determined, i.e. the classiﬁer j

∗

corresponding to

the highest output value o(j

∗

) is chosen such that

∗

= argmax

j=1..s

(o(j)). Thus a path through the

hierarchy from the root node to an end node is ob-

tained which not only represents the class of the ob-

ject but also the subsets of classes to which the ob-

ject belongs. Hence the data point is not presented to

all classiﬁers within the hierarchy and the hierarchi-

cal decomposition of the classiﬁcation problem yields

additional intermediate information.

If only intermediate results are of interest it might

not be necessary to evaluate the complete path. In

order to solve a task it might be sufﬁcient to know

whether the object to be recognised belongs to a set

of classes and the knowledge of the speciﬁc category

of the object might not add any value. If the task for

example is to grasp a cup, it is not necessary to dis-

tinguish between red and green cups. Moreover, when

looking for a speciﬁc object it might in some cases not

be necessary to retrieve the ﬁnal classiﬁcation result

if a decision at a higher level of the hierarchy already

excludes this object.

2.4 Incremental Learning of New

Classes

While performing tasks a robot is likely to encounter

unfamiliar objects. Hence the ability to learn new

objects plays an important role. Given the situa-

tion that an object is in the robot’s visual ﬁeld and

it is told the name of the new object by an instruc-

tor, the robot might look at the object from different

points of view and thereby generate a few data sam-

ples

S := {(x

, ˜c), ν = 1, ..., N } of the new class

˜c /∈ C. So compared to the already known classes

C the number of samples N of the new class ˜c is ap-

preciably lower. This scenario forms the basis for the

incremental learning approach developed here. In the

overall system the online learning is triggered by in-

struction sentences starting with ”this is” followed by

an object name.

In order to quickly achieve results the learning is

performed in two stages. In the ﬁrst stage fast but

less sophisticated methods are used to obtain initial

results, i.e. the novel objects are learnt but the recog-

nition rate might be weak. In this ﬁrst stage the recog-

nition rate can be improved by using a similar method

to retrain the new object with additional data gained

by taking different views of the object. In a second

stage more complex algorithms are used to adapt the

system and to further improve the classiﬁcation re-

sults. This retraining is more advanced but also more

time consuming.

At ﬁrst it is necessary to identify whether the pre-

sented object is already known or not. This is accom-

plished by presenting the new data to the trained clas-

siﬁer and taking the strength of the classiﬁer response

into account. Thereby a strong response is consid-

ered as an unambiguous decision and weak responses

indicate a dubious decision which could be evoked

by unknown classes or if the object to classify bears

resemblance to more than one class. The thresholds

for this are derived from the classiﬁer responses when

testing the known data. If the new data is unambigu-

ously classiﬁed as one class c without exception it is

assumed that the object is already known and belongs

to class c. Otherwise the object is regarded as a hith-

erto unidentiﬁed object.

If an object is identiﬁed as unfamiliar it is learnt by

ﬁtting it into the hierarchy and if necessary retraining

the affected nodes. The new class ˜c /∈ C associated

with the unknown object is inserted as a new leaf. The

position of the new leaf is determined by classifying

all new data and evaluating the corresponding paths

through the hierarchy. The leaf will be inserted where

the paths start to diverge. As complete identicalness

for all data cannot be presumed even at the root node

since the network has not been trained with this data

a certain variance needs to be considered. Otherwise

ICINCO 2005 - ROBOTICS AND AUTOMATION

300

the new leaf would in most instances be added at the

root node. Therefore the common path is successively

determined similar to retrieving the classiﬁcation re-

sult. Starting with the root node all new samples are

presented to the corresponding classiﬁer. Depending

on the classiﬁcation results either the next node in the

path is determined or the search is stopped and the

new class is added as a new leaf at this node. If all

new samples x

are assigned to one successor node

j by classiﬁer i node i is added to the common path

without retraining and classiﬁer j is the next classiﬁer.

If not all but a signiﬁcant majority of the data points

is assigned to the same successor node j this classiﬁer

is retrained using the samples of the known objects as

well as the new samples and node i is then added to

the common path. If there is no clear decision or if

all successor nodes of node i are end nodes the new

class is added as an additional end node to this node

and the node is afterwards retrained. Because of the

way the hierarchy is built only part of the hierarchical

classiﬁer needs to be amended. The rest of the hierar-

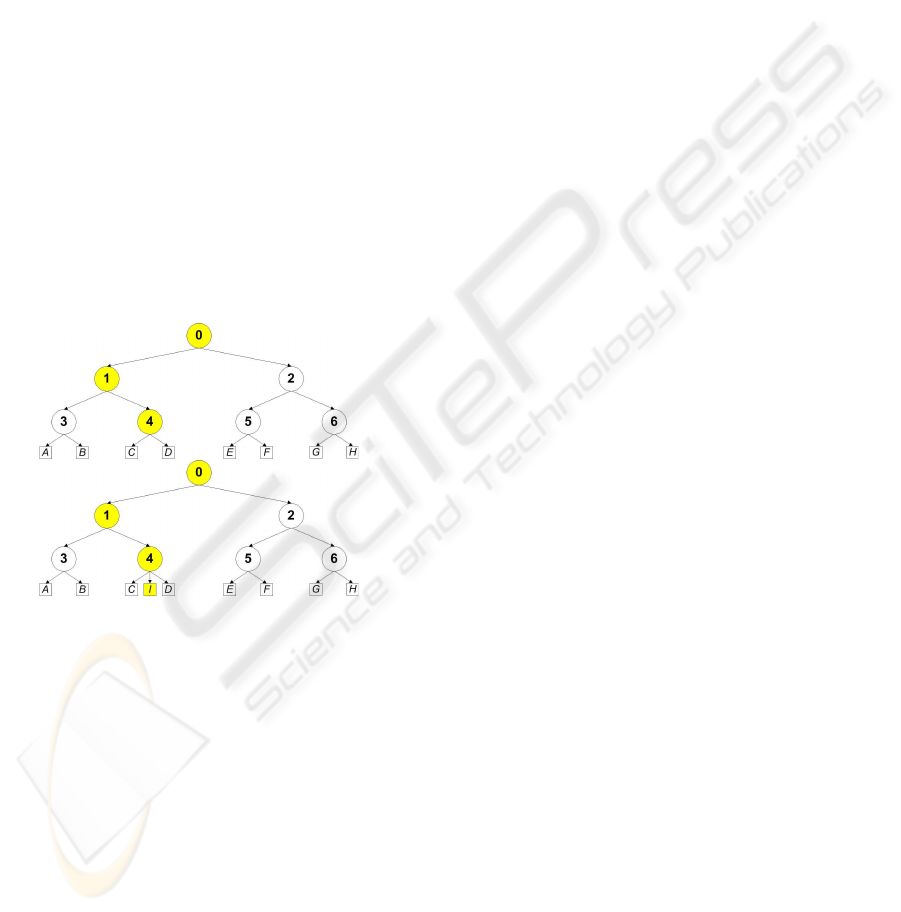
chy remains unchanged. Figure 2 depicts how a new

class is inserted into the hierarchy by means of the

proposed incremental learning approach.

Figure 2: Example of the incremental learning of a new

class I. At ﬁrst the position where to insert the new class

is determined. Then the new class is added as a new leaf

and the affected nodes are retrained. Here the new class is

added to node 4. The classiﬁers 0 and 1 are retrained with

the samples of the additional class I. One additional node is

added to the output layer of classiﬁer 4 and the classiﬁer is

then retrained.

The retraining or incremental training of the classi-

ﬁers is conducted by adding a new neuron to the hid-

den layer and then retraining the output weights with

the joint sample set of old and new samples. The cen-

tre of the new prototype is determined by the mean

of all new samples. The width of the corresponding

gaussian function is set to the mean distance of the

new samples to the centre and the new output weights

are learnt by calculating the pseudo-inverse (Penrose,

1955).

A similar mechanism is applied when retraining al-

ready learnt classes. The only differences are that no

additional leaf is added and that the path through the

hierarchy is already known. The single classiﬁers on

this path are retrained if there are any incorrect or am-

biguous decisions.

Scenarios for retraining an already learnt class

could be when a class is only represented by few sam-

ples or the classiﬁcation performance for this class

is not satisfactory. The classiﬁcation rate of novel

classes is likely to be lower than the classiﬁcation rate

for the previously learnt classes. Thus a retraining

of all affected nodes can yield improved classiﬁca-

tion results once sufﬁcient additional samples for the

novel class are available. Another reason could be

that a new instance of a class with noticeably differ-

ent characteristics has to be learnt.

The online learning phase is followed by an ofﬂine

learning phase where more sophisticated learning al-

gorithms such as three phase learning are used which

will further improve the classiﬁcation performance.

All nodes to which the novel classes have been as-

signed are newly trained. These algorithms would be

too time consuming for usage during run time.

This incremental learning approach can also be

used for non-hierarchical neural networks. However,

here it is not necessary to determine the position were

to insert the new leaf as non-hierarchical networks can

be regarded as hierarchical networks consisting only

of one node, but a retraining of the complete network

takes place whereas only parts of the hierarchical net-

work is amended.

3 RESULTS

By means of classiﬁcation experiments the suitabil-

ity of hierarchical neural networks for extension was

examined. It should be veriﬁed whether new classes

that are only represented by a few samples can be

learnt sufﬁciently well in moderate time and whether

it is possible to learn new classes without negatively

affecting the classiﬁcation performance of already

learnt classes.

The incremental learning approach has been eval-

uated using the Columbia Object Image Library

(COIL20) (Nene et al., 1996) consisting of 20 ob-

jects. Therefore 10-times 10-fold cross-validation ex-

periments have been conducted on the camera images

of the COIL20 image library.

Another approach for learning new objects would

be a complete redesign of the classiﬁer. This means

that everything learnt so far is dropped and the clas-

siﬁer is rebuild and trained with the joined samples

of the known and unknown objects. For the classiﬁer

training only simple training algorithms such as two-

INCREMENTAL LEARNING IN HIERARCHICAL NEURAL NETWORKS FOR OBJECT RECOGNITION

301

phase learning (Schwenker et al., 2001) can be used as

sophisticated learning algorithms would be too time-

consuming and hence not applicable for online learn-

ing. Compared to the incremental learning approach

this method features longer training time as a com-

plete rebuild of the hierarchy and training of all nodes

within the hierarchy are required. The approach pro-

posed has been compared to this method.

In order to facilitate comparability of the results of

the different approaches for all experiments the same

division of the data for the cross-validation has been

used.

For the experiments 10 classes of the 20 classes of

the COIL20 data set were chosen to represent the fa-

miliar objects. The remaining 10 classes formed a

pool of potentially new objects. To test the incre-

mental learning approach proposed the ﬁrst 10 classes

were used to generate and train a hierarchy. To train

the hierarchy sophisticated learning algorithms were

used. Here the three-phase learning for RBF networks

was used. The hierarchy structure was held constant

for reasons of comparability while the hierarchy train-

ing was subject to cross-validation. This means the

same hierarchy was trained 10 × 10 times resulting

in 100 trained hierarchies. These trained hierarchies

for the classiﬁcation of the ﬁrst 10 classes formed the

basis for the incremental learning experiments. Each

of the 10 new classes was then learnt incremental so

that 10 × 10 × 10 hierarchies for the classiﬁcation of

11 classes emerged. For the incremental learning 10

samples of the unknown class were used compared

to 64 to 65 samples (depending on the speciﬁc cross-

validation run) of the other classes. In the test data set

all classes are represented with the same number of

samples.

With the same partition of the samples the alterna-

tive method which completely rebuilds the hierarchy

was evaluated. Therefore 10 hierarchies for the clas-

siﬁcation of 11 classes each were generated. For each

of the 10 hierarchies 10 × 10 cross validation experi-

ments were conducted.

Both approaches showed essentially the same clas-

siﬁcation quality. The incremental learning approach

had an average classiﬁcation rate of 95.94 ± 2.96%

and the average classiﬁcation rate of the alternative

method was 95.54 ± 2.56%. Despite being less exten-

sive the incremental learning approach achieved the

same results. Figure 3 visualises these results as box

plots.

The confusion matrix for the incremental learning

experiments displayed in ﬁgure 4 shows that although

being represented by a signiﬁcantly lower number of

samples the classiﬁcation rates of the new classes is

equal to the classiﬁcation rates of the primarily learnt

classes.

Having a look at the positions within the hierarchy

were the new classes were added, it could be found

Figure 3: Box plot of the classiﬁcation results of the two

alternative approaches for learning new classes. The classi-

ﬁcation results do not differ signiﬁcantly.

Figure 4: Confusion matrix for the experiments utilising

incremental learning.

that in the most instances a class was mainly assigned

to one node. If this is not the case then at least the

class was added to nodes lying on the same path of

the hierarchy as can be observed for class 13. The

only exception to this is class 11, which is distributed

over different pathes of the hierarchy. It can also be

observed that in the majority of cases the classes were

added to nodes in deeper levels of the hierarchy. No

classes were added to the root node. Figure 5 illus-

trates for each new class how often it was added to

which node of the hierarchy shown in ﬁgure 1.

These results show that the new classes are not

added arbitrarily to the hierarchy but for each class

preferred positions emerge. The noticeable frequency

of node 8 is likely to be a characteristic of the COIL20

data set.

4 RELATED WORK

An example for other incremental learning ap-

proaches are ART networks. ART networks (Gross-

berg, 2000) (Carpenter and Grossberg, 2002) allow

for online learning of evolving data sets. If a pre-

sented sample is similar enough to an learnt proto-

type this prototype is adjusted to the sample, other-

wise a new prototype is deﬁned by the sample. In the

ARAM model (Tan, 1995) new classes can be learnt

ICINCO 2005 - ROBOTICS AND AUTOMATION

302

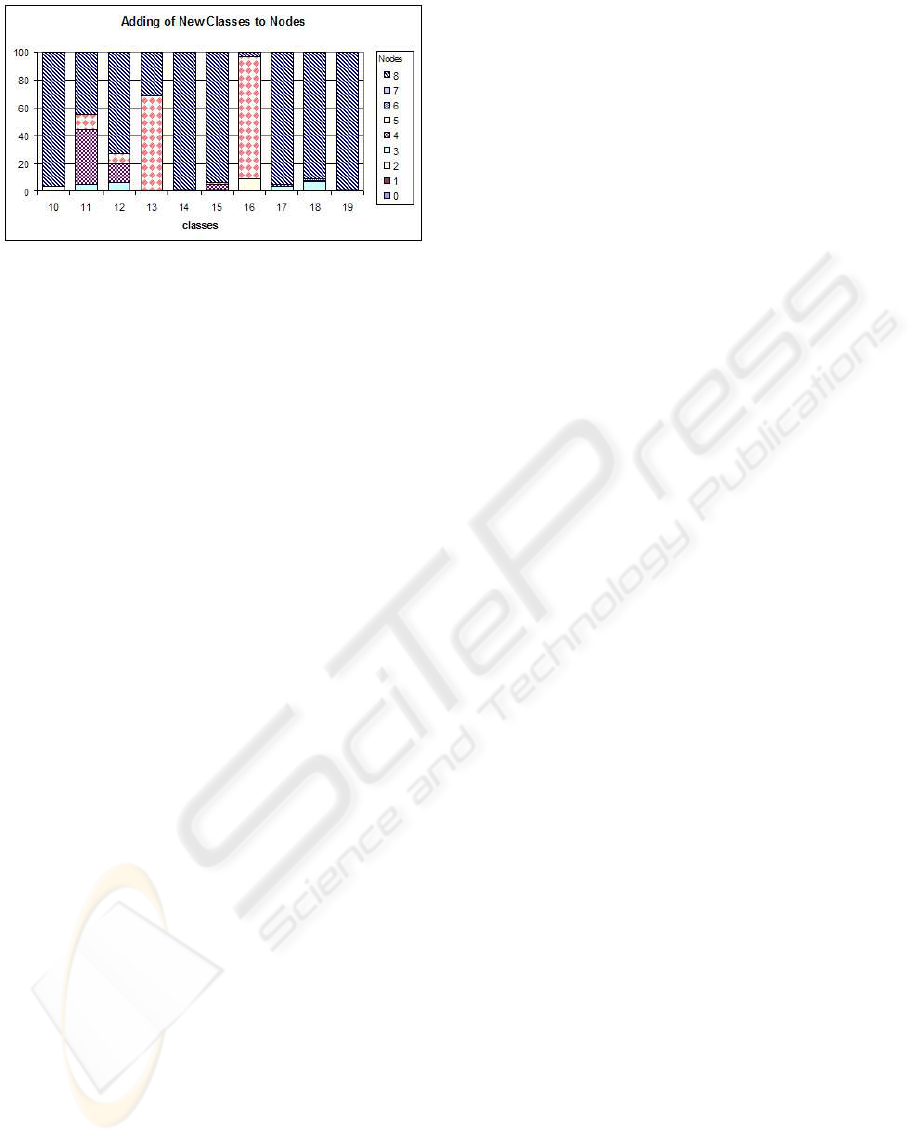
Figure 5: Adding of new classes to nodes. For each of the

10 × 10 cross-validation experiments conducted for each of

the new classes 10 to 19 a leaf was added to different nodes

of the classiﬁcation hierarchy. For each new class is shown

in percent to which node the corresponding leaf was added.

while preserving previously learnt classes and so the

stability-plasticity dilemma is regarded. However,

ART networks are non-hierarchical networks and they

consider new samples one at a time.

5 CONCLUSIONS

The proposed approached has proven functional. Al-

though the networks were trained with only a few

samples of the new classes they were able to classify

the new class and no considerable deterioration of the

classiﬁcation results of the former classes could be

observed.

The experiments conducted showed encouraging

results. It could be proved that hierarchical neural net-

works are suitable for incremental adaption. New ob-

jects can be learnt with sufﬁcient classiﬁcation rates

and in adequate time.

The proposed approach enables the robot to deal

with varying object categories in addition to the pre-

deﬁned categories. New objects can be learnt rather

quickly with satisfactory quality. The quality can even

be increased by retraining with additional samples

and in an ofﬂine phase sophisticated learning algo-

rithms are used to further improve the classiﬁcation

quality.

ACKNOWLEDGEMENT

This research was supported in part by the Euro-

pean Union award #IST-2001-35282 of the MirrorBot

project.

REFERENCES

Carpenter, G. A. and Grossberg, S. (2002). Adaptive Res-

onance Theory. In Arbib, M., editor, The Handbook

of Brain Theory and Neural Networks, pages 87–90.

MIT Press, Cambridge, 2nd edition.

Coppola, D. M., Purves, H. R., McCoy, A. N., and Purves,

D. (1998). The distribution of oriented contours in the

real world. Proceedings of the National Academy of

Sciences USA, 95(7):4002–4006.

Duda, R. O., Hart, P. E., and Stork, D. G. (2001). Pattern

Classiﬁcation. John Wiley & Sons, New York, 2nd

edition.

Fay, R., Kaufmann, U., Schwenker, F., and Palm, G. (2004).

Learning object recognition in an neurobotic system.

3rd IWK Workshop SOAVE2004 - SelfOrganization of

AdaptiVE behavior, Illmenau, Germany, pages 198–

209.

Freeman, W. T. and Roth, M. (1995). Orientation his-

tograms for hand gesture recognition. In IEEE Inter-

national Workshop on Automatic Face- and Gesture-

Recognition, pages 296–301, Z

urich, Switzerland.

Grossberg, S. (2000). Adaptive resonance theory. Tech-

nical Report TR-2000-024, Center for Adaptive Sys-

tems and Department of Cognitive and Neural Sci-

ence, Boston University.

Knoblauch, A., Fay, R., Kaufmann, U., Markert, H., and

Palm, G. (2004). Associating Words to Visually

Recognized Objects. In Coradeschi, S. and Safﬁotti,

A., editors, Anchoring symbols to sensor data. Papers

from the AAAI Workshop. Technical Report WS-04-03,

pages 10–16. AAAI Press, Menlo Park, California.

Nene, S. A., Nayar, S. K., and Murase, H. (1996). Columbia

object image library (coil-20). Technical Report Tech-

nical Report CUCS-005-96, Columbia University.

Penrose, R. (1955). A generalized inverse for matrices.

Mathematical Proceedings of the Cambridge Philo-

sophical Society, 51:406–413.

Schwenker, F. (2001). Solving multi-class pattern recogni-

tion problems with tree structured support vector ma-

chines. In Radig, B. and Florczyk, S., editors, Muster-

erkennung 2001, pages 283–290. Springer.

Schwenker, F., Kestler, H. A., and Palm, G. (2001). Three

learning phases for radial-basis-function networks.

Neural Networks, 14:439–458.

Simon, S., Schwenker, F., Kestler, H. A., Kraetzschmar,

G. K., and Palm, G. (2002). Hierarchical object

classiﬁcation for autonomous mobile robots. In In-

ternational Conference on Artiﬁcial Neural Networks

(ICANN), pages 831–836.

Tan, A.-H. (1995). Adaptive resonance associative map.

Neural Networks, 8(3):437–446.

INCREMENTAL LEARNING IN HIERARCHICAL NEURAL NETWORKS FOR OBJECT RECOGNITION

303