
GA BASED DATA FUSION APPROACH IN AN INTELLIGENT
INTEGRATED GPS/INS SYSTEM
Ali Asadian, Behzad Moshiri
Control and Intelligent Processing Center of Excellence
Department of Electrical and Computer Engineering, University of Tehran, Tehran, Iran
Ali Khaki Sedigh
Control and Intelligent Processing Center of Excellence
Department of Electrical Engineering, University of K.N.T, Tehran, Iran
Caro Lucas
School of Cognitive Sciences, Institute for Studies on Theoretical Physics and Mathematics
Tehran, Iran
Keywords: Genetic optimization, Adaptive Network based Fuzzy Inference System (ANFIS), Global Positioning
System (GPS), Inertial Navigation System (INS).
Abstract: A new concept regarding to the GPS/INS integration, based on artificial intelligence here is presented. Most
integrated inertial navigation systems (INS) and global positioning systems (GPS) have been implemented
using the Kalman filtering technique with its drawbacks related to the need for predefined INS error model
and observability of at least four satellites. Most recently, an INS/GPS integration method using a hybrid-
adaptive network based fuzzy inference system (ANFIS) has been proposed in literature. During the
availability of GPS signal, the ANFIS is trained to map the error between the GPS and the INS. Then it will
be used to predict the error of the INS position components during GPS signal blockage. As ANFIS will be
employed in real time applications, the change in the system parameters (e.g., the number of membership
functions, the step size, and step increase and decrease rates) to achieve the minimum training error during
each time period is automated. This paper introduces a genetic optimization algorithm that is used to update
the ANFIS parameters with the INS/GPS error function used as the objective function to be minimized. The
results demonstrate the advantages of the genetically optimized ANFIS for INS/GPS Integration in
comparison with conventional ANFIS specially in the cases when facing satellites’ outages. Coping with
this problem plays an important role in assessment of the fusion approach in land navigation.
1 INTRODUCTION
Ever since the artificial intelligence, has been
considered as a powerful and applicable tool in
engineering modeling, computation, nonlinear
function approximation, system identification and
estimation theory. The neuro-fuzzy models have the
connectionist structure of neural networks combined
with flexibility and intuitive learning capabilities of
fuzzy systems. A variety of Inference engines and
learning algorithms have been discussed in the
literature (Mackay, 2003). ANFIS is one of the most
popular algorithms that has been used for different
purposes such as system identification, signal
processing, pattern recognition, control of dynamical
systems and prediction (Shing et al., 1993). As
discussed it has a hybrid learning method based on
gradient descent and least square estimation.
Another new method which can be categorized in
the intelligent approaches is genetic algorithms. GAs
as function optimizers are global optimization
techniques based on natural selection (Goldberg,
1989 ; Michalewicz, 1996). This form of
evolutionary algorithm evolves throughout
generations improving the features of potential
216
Asadian A., Moshiri B., Khaki Sedigh A. and Lucas C. (2005).
GA BASED DATA FUSION APPROACH IN AN INTELLIGENT INTEGRATED GPS/INS SYSTEM.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 216-221
DOI: 10.5220/0001171802160221
Copyright
c
SciTePress
solutions by means of biologically inspired
operations. GAs are presented as a tool to optimize a
certain objective function. For instance in GAs have
been combined with extended kalman filter in order
to increase the overall performance (Stroud, 2001).
Several usages of GAs have been found in the
literature (Geisler et al., 2002 ; Loebis et al., 2003 ;
Simske, 2003). Here in this paper we will focus on
optimization of the ANFIS network with GAs in the
field of navigation applications. It will be shown that
the mentioned estimator filter has an excellent
performance when encountering satellites’ outage as
a great benchmark in assessment of fusion approach.
2 OVERVIEW
It’s well established that global positioning system
(GPS) can provide position and velocity information
of moving platforms with consistent accuracy
throughout the surveying mission. The limitations of
GPS are related to the loss of accuracy in the
narrow-street environment, intentional disruption of
the service, poor geometrical-dilution-of-precision
(GDOP) coefficient and the multipath reflections.
GPS-based navigation system requires at least four
satellites, so a major drawback of GPS dependence
navigation systems is that their accuracy degrades
significantly with satellites’ outages. Signal outage
is more significant for land vehicle positioning in
urban centers, which takes place when encountering
highway overpasses or tunnels. Besides the presence
of noise in GPS signals, necessitates the use of
narrow bandwidth filters which limits also the
dynamic of the vehicle. So it is suitable to integrate
this type of navigation system with a different type
of navigation system in order to reach a greater
autonomy.
From this point of view, the inertial navigation
system (INS) is ideal. In opposition with receiving
signals from satellites, in the case of GPS, the
autonomy of INS is provided by the functioning
principle, which is based on measurements of inertia
of the vehicle, linear accelerations, and angular
velocities. An INS measures the linear acceleration
and angular rates of moving vehicles through its
accelerometers and gyroscopes sensors. The main
interest is the position determination, which is
possible after a double integration of the
accelerations to obtain linear displacements and a
single integration of the angular velocities to obtain
the angles of rotation. The INS accuracy degrades
over time, due to the unbounded positioning errors
caused by the uncompensated gyro and
accelerometer errors affecting the INS
measurements. The degradation is much faster for
low-cost INS systems. INS provides high-accuracy
three-dimensional positioning when the GPS
positioning is poor or unavailable over short periods
of time (e.g., due to poor satellite geometry, high
electromagnetic interference, high multipath
environments, or obstructed satellite signals). In
addition, the INS system provides much higher
update positioning rates compared with the output
rate conventionally available from GPS (Farrel,
1999). Anyway in order to utilize the benefits of
these two navigation sensors and gain the
advantages of the data fusion, we fuse the data
gathered by each and use integrated system.
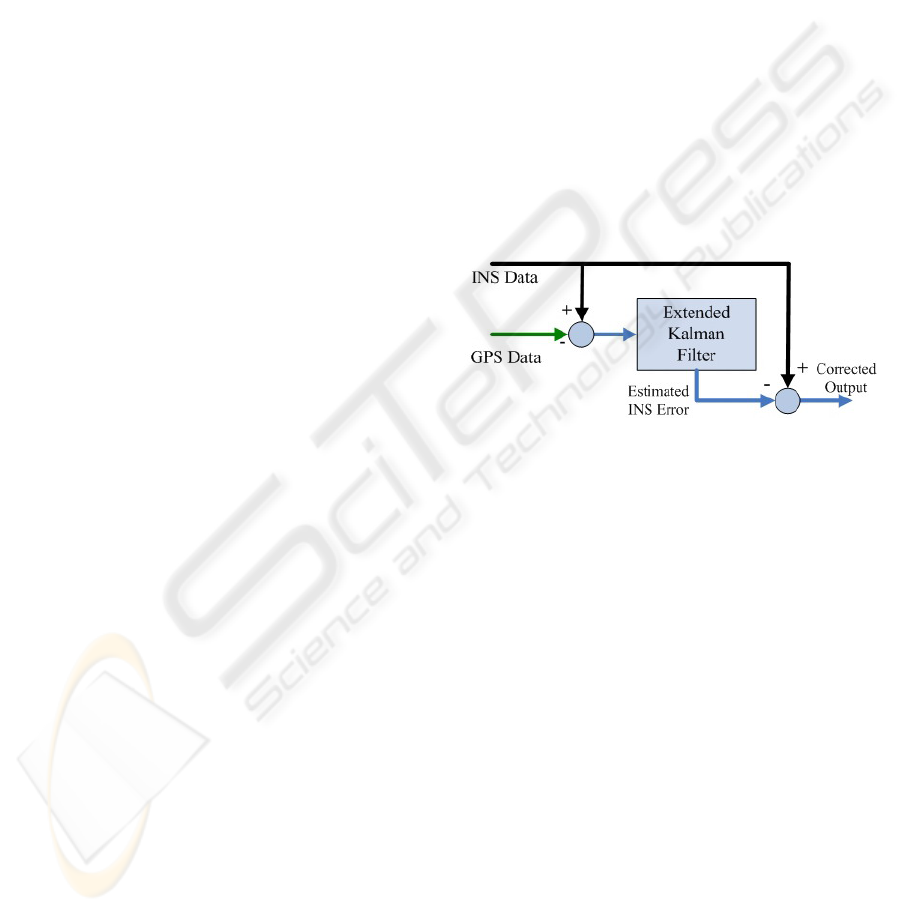
Traditional integration which is accomplished by
means of Kalman filtering has been shown in Figure
1. Where the INS outputs are compared to the
outputs of the GPS. The errors in between are
subjected to Kalman filtering, which enhances the
performance of the navigation system by removing
the effect of residual random errors during the
surveying process (Mayhew, 1999).
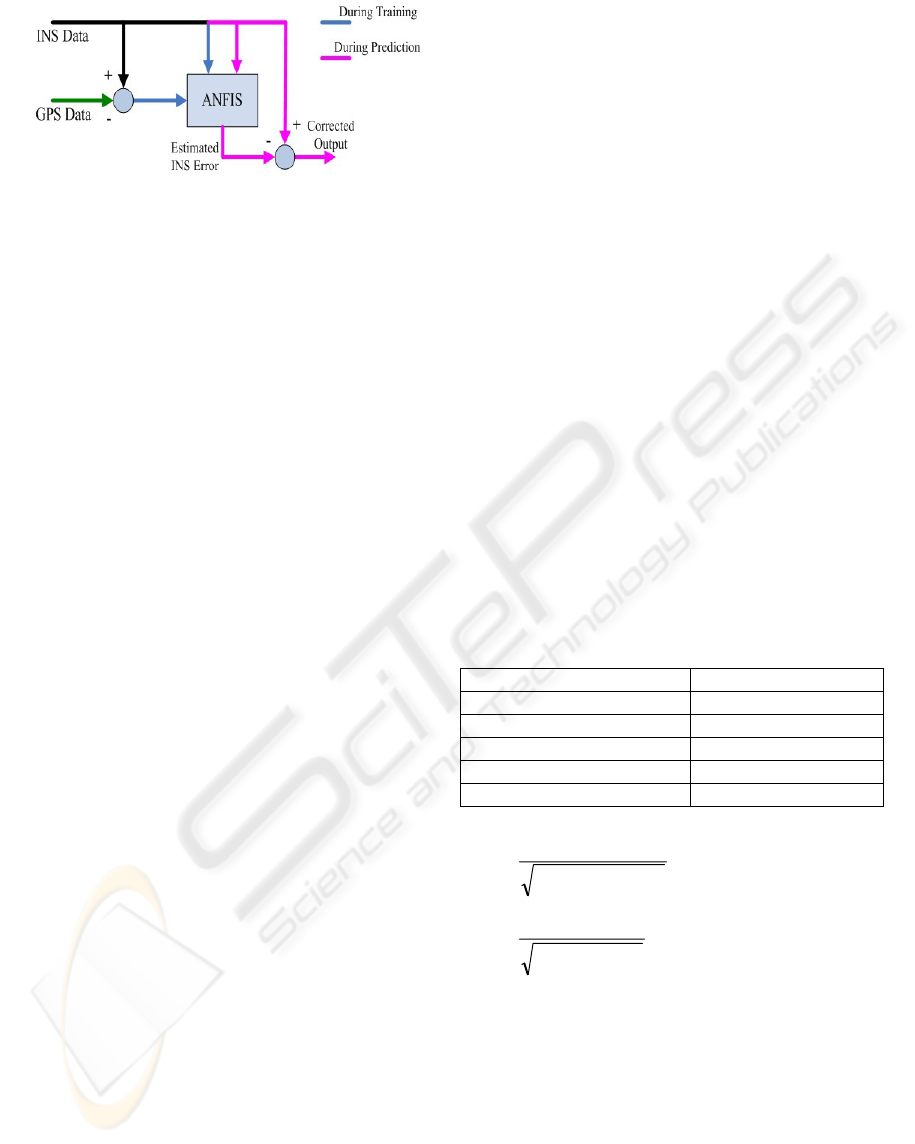
As mentioned in the literature, Kalman filter
provides poor prediction of position errors, when
encountering satellites’ outages. In order to prevent
or, at least, to reduce the impact of accuracy
decreasing when GPS becomes unavailable, an
adaptive network based fuzzy inference system
(ANFIS) has been used on a simplified 2-
Dimensional navigation model, built and trained
using data from stand-alone INS, on one hand, and
from the GPS on the other hand (Hiliuata et al.,
2004). For this purpose, the GPS-derived positions
and velocities are excellent external measurements
for updating the INS, thus improving its long-term
accuracy. This fact has been illustrated in Figure 2.
The ANFIS could be built and trained during the
availability time of reference system. Passing the
INS data through ANFIS will procure a better
accuracy when the reference source is missing. In
the absence of the GPS information, the system will
perform its task only with the data from INS and
with the intelligent correction algorithm. A complete
investigation has been performed to solve the
navigation problem with real data via ANFIS
network (Wang et al., 2003).
Figure 1: Traditional GPS/INS integration using
Kalman filtering
GA BASED DATA FUSION APPROACH IN AN INTELLIGENT INTEGRATED GPS/INS SYSTEM
217
3 GENETIC ALGORITHM
OPTIMIZATION
The GAs behave much like biological genetics and
are an attractive class of computational models that
mimic natural evaluation to solve problems in a
wide variety of domains (Luke et al., 1998). They
introduce a population of individual solutions to an
optimization problem and then evaluate the fitness
of each individual in this population. Limited by the
laws of natural selection, individuals with most
suited elements in a population and better
performance survive while those with weak
performance are weeded out. The optimization
process gets its dynamic by developing new
generations of potential solutions and evaluating the
degree of fitness of each generation and allowing it
to proceed if it satisfies specific selection criterion
which is usually based on a fitness-proportional
selection.
GAs map a problem onto a set of strings (the
chromosomes), each string representing a potential
solution. The three most important aspects of using
GAs are :
• definition of the objective function
• definition and implementation of the
genetic representation
• definition and implementation of the
genetic operators
The speed of genetic algorithm depends heavily
on the encoding scheme of the chromosomes and on
the genetic operators that work on these
chromosomes (Geisler et al., 2002).
The following is a pseudo code for a general
GA :
• Generate the initial parent population
• Evaluate the initial parent population
• Loop until termination criteria is satisfied
• Select chromosomes for reproduction
• Create offspring using reproduction
operators such as crossover and
mutation
• Replace parent population by offspring
population
• Return fittest chromosome of last parent
population
4 MATHEMATICAL MODEL OF
INTEGRATED GPS/INS
SYSTEM
Several mathematical models have been proposed in
order to integrate INS and GPS sensors (He, et al. ,
1998). The number of states generally determines
the accuracy of the modeling. Different models have
been utilized in the literature. Here we use the model
explained below (Azimi-Sadjadi, 2001).
Measurements of accelerometers and gyros are
expressed in the platform frame while the GPS
measurements are given in an rectangular Earth
Centered Earth Fixed (ECEF) frame. The geodetic
coordinate system is defined according to the
familiar longitude (
λ
), latitude(
φ
), and height( h )
coordinate system. For this system of coordinates,
the Earth’s geoid is approximated by an ellipsoid.
The defining parameters for the geoid according to
the WGS84 reference frame are given in Table 1.
and equations (1-2). The relation between these two
coordinate system is also given by (3).
Value Parameter
6378.137 km a (semi major axis)
6345.752 km
b (semi minor axis)
7.292115×10
−5
Rad/Sec
ie
ω
(earth's angular velocity)
3.352511×10
−3
f (ellipsoid's flatness)
0.05781 e (ellipsoid's eccentricity)
322
2
)}(sin1{
)1(
φ
λ
e
ea
R
−
−
=
(1)
)(sin1
22
φ
φ
e
a
R
−
=
(2)
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+−
+
+
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
)sin())1((
)sin()cos()(
)cos()cos()(
2
λ
φλ
φλ
φ
φ
φ
heR
hR
hR
Z
Y
X
m
m
m
(3)
For simplicity we assume that the gyros and the
accelerometers are aligned with the axis in the
platform frame. Also, we assume that the body
frame and the platform frame are aligned, and the
center of the coordinate system is the same for both
frames. The transformation from body frame to local
Figure 2: Intelligent GPS/INS integration with ANFIS
Table 1: Parameters of WGS84 reference frame
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
218

geographical frame is calculated at every moment as
follows :
dtRdR
b
gbgbgb
Ω=
22
(4)
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
−
=Ω
0
0
q 0
pq
pr
r
b
gb
(5)
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
+−
+
−
+
+
−
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=
hR
V
hR
V
hR
V
R
b
b
b
r
q
p
r
q
p
E
ie
N
E
ie
bg
r
q
p
b
gb
λ
φ
λ
φ
φω
φω
ω
)tan(
)sin(
)cos(
~
~
~
2
(6)
b
gb
ω
is the inertial angular rate expressed in the
body frame which can be expressed as follows in
(6), where
T
rqp )
~
~
~
(
is the measured angular rate, and
T
rpq
bbb ) (
is the bias in the angular rate
measurement.
The GPS signal consists of a clock signal and a
navigation message that are amplitude modulated.
The GPS receiver receives the signal corrupted by
noise and other sources of error. By neglecting the
ionospheric and tropospheric errors which are highly
correlated, the observation equations or
pseudoranges provided by
th
i GPS satellite, have
the following form :
δρ
cZZYYXX
msimsimsii
+−+−+−=
222
)()()(
(7)
where
),,(
mmm
ZYX and ),,(
sisisi
ZYX are the
coordinates of the receiver and the
th
i satellite
respectively.
c is speed of the light and
δ
equals
clock drift.
Note that the above hypothesis is valid in most
land navigation purposes. In order to simplify the
design process in future, it’s assumed that the
receiver coordinates in ECEF frame can be extracted
from the pseudoranges through out the use of an
external extended kalman prefilter. We suppose this
fact for the rest of this research so the outputs of the
GPS sensor are supposed to be the receiver’s
coordinates. The GPS clock drift and the INS
equations constitute key dynamics in an integrated
INS/GPS system and could be expressed as (8-13)
equations. where g is the gravitational acceleration,
T
wvu
aaa )
~
~
~
(
is the accelerometer measurement
expressed in the body frame,
T
wvu
bbb ) (
is the
accelerometer measurement bias again expressed in
the body frame.
v
t
w ,
x
t
w ,
1
b
t
w and
2
b
t
w are vectors of
brownian motion process with zero means and
known covariance matrixes.
dt
V
V
V
hR
hR
h
d
D
E
N
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
−
+
+
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
1 0 0
0
)cos()(
1
0
0 0
1
φ
λ
φ
λ
φ
{}
v
t
w
v
u
w
v
u
gb
E
Eie
N
DE
DNie
NE
DN
Eie
E
D
E
N
dwdt
g
b
b
b
a
a
a
R
dt
hR
V
V
hR
V
hR
VV
VV
hR
VV
hR
VV
V
hR
V
V
V
V
d
+
⎪
⎭
⎪
⎬
⎫
⎪
⎩
⎪
⎨
⎧
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
+
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
+
−−
+
−
+
+++
+
+
+−
+
−
=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
0
0
~
~
~
)cos(2
)cos(2)sin(
)tan(
)sin(2
)tan(
2
2
2
2
λφ
λφ
φλ
φω
φφω
φ
φω
φ
1
1
b
t
w
v
u
w
v
u
dwdt
b
b
b
b
b
b
b
d +
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
2
2
b
t
r
q
p
r
q
p
dwdt
b
b
b
b
b
b
b
d +
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
x
ttt
dwdtaxdx +−=
dtxd
t
=
δ
(8-13)
5 ARCHITECTURE OF THE
PROPOSED NETWORK
In the previous studies the ANFIS parameters (
β
as
step size,
I
β
as step increase rate and
D
β
as step
decrease rate) were tuned manually by trial and error
to prove the efficiency of ANFIS network for
INS/GPS integration (Wang et al., 2003). Changing
these parameters could significantly affect ANFIS
prediction capabilities and have considerable effect
in our application while changing the number of
fuzzy rules is unlikely to produce any significant
impact. Therefore, these parameters’ tuning process
should be automatized to allow system utilization in
real-time applications so it’s suggested here that
ANFIS network parameters shall be tuned
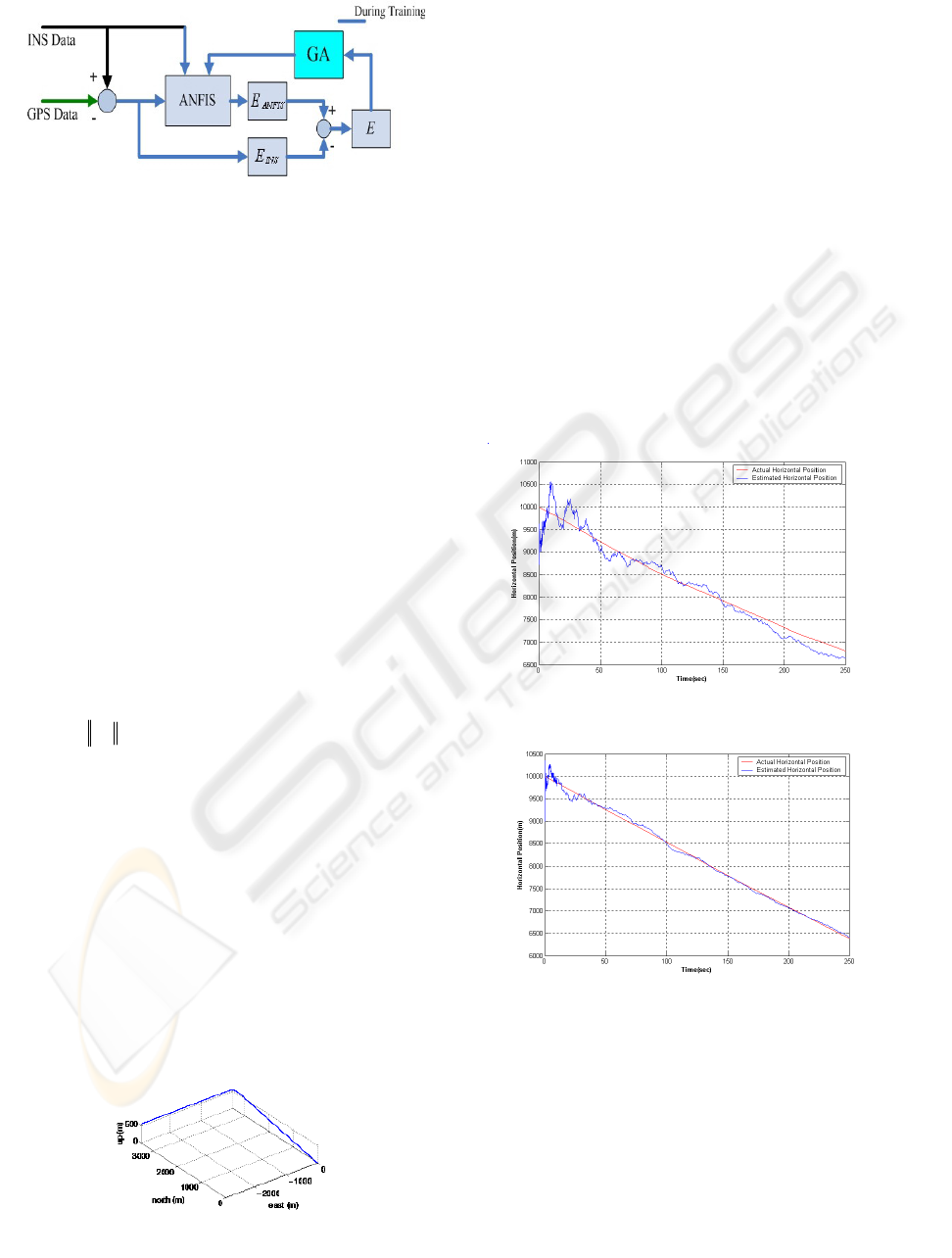
automatically by means of genetic algorithms. It’s
proposed that a GA to be used to optimize ANFIS
network parameters during the training mode with
the objective of achieving the minimum training
error. This new scheme has been illustrated in Figure
3. The proposed automatization process will cause
considerable reduction of position error than those
reported before.
GA BASED DATA FUSION APPROACH IN AN INTELLIGENT INTEGRATED GPS/INS SYSTEM
219
17 separate ANFIS networks were developed for
integrating the INS/GPS for the whole state vector
components. All the networks have similar
architecture but different parameters. During the
training process, the mentioned parameters can be
tuned for each network separately to achieve the
minimum training error for each time period and for
each state vector component. In the training mode
the network’s inputs include INS outputs and time
(T) while its desired output is
INS
E as described in
equation (14) where
P
denotes the corresponding
position. The system concept is to train the network
during the GPS availability periods and then to
predict the INS error signal once the GPS outage
occurs.
INSGPSINS
PPE −= (14)
….After training process, the ANFIS network will
produce an INS error, which can be denoted as
ANFIS
E . Then the modeling error is defined as (15) :
ANFISINS
EEE −= (15)
….Then by defining the root mean square of the
model error for n observations as (16) :
2
ERMSE = (16)
….The objective function for the GA is chosen to
minimize the RMSE by optimizing ANFIS network
parameters.
6 SIMULATION RESULTS
The simulation was made with a relatively low IMU
sample rate, 10 Hz. The GPS pseudoranges are
available with the rate of 1 Hz. The kinematic data
used in this study was generated by Satnav toolbox
created by GPSoft. In our test, the following flight
profile was used. This flight path (Figure 4)
contains one pitch manoeuver in the beginning and
one 90 degree turn in the middle of scenario
.
The numerical parameters were selected as
below. The last parameters model a typical quartz
TCXO with frequency drift rate of
secsec/10
9−
.
I
b
w
-4
10905.4
1
×=
∑
,
I
b
w
0.09
2
=
∑
,
I
v
w
-5
10=
∑
,
0015.0
21
=
=
bb
,
12
10
−
=
x
w
σ
,
002.0
=
a
.
The GA was implemented using a genetic
algorithm optimization toolbox developed in
MATLAB 7 package. The algorithm utilized a
crossover rate of
c
ρ
=0.75 and a probability of
mutation of
m
ρ
=0.001. The proposed network was
trained using the GA architecture described before.
18 generations were created by the GA algorithm to
search for the minimum RMSE. The search
converged successfully to the minimum RMSE after
18 generations. The ability of the two networks in
correct prediction is compared in Figures 5 and 6.
It’s clear that the second network’s output is a little
bit better than the first one’s.
The optimal parameters that led to the minimum
of RMSE are :
β
=0.0298,
I
β
=1.6935 and
D
β
=0.6221. After completion the training process,
then a complete GPS signal outage of 120 seconds
starting at time 450 was intentionally introduced
within the GPS data and both algorithms were used
to predict the INS dynamic during the outage period.
In order to save computational effort, in this case
GA optimization is only applied during satellites’
Figure 3: Intelligent GPS/INS integration with optimized
ANFIS with GA
Fi
g
ure 4: The fli
g
ht scenario
Figure 5 : Position tracking of the ANFIS
Figure 6: Position tracking of the optimized ANFIS
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
220
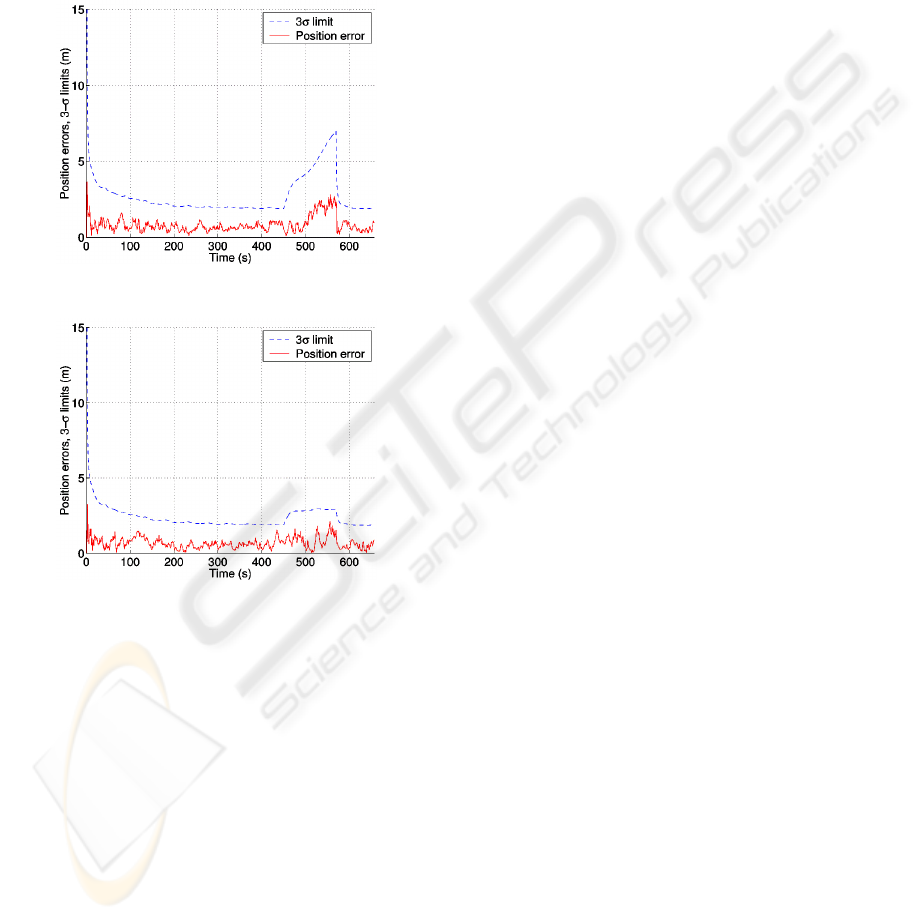
outage. The RMSE of the two networks during this
period were obtained as 2.684 for ANFIS and 1.123
for optimized ANFIS versus meters.
It is obvious that the second network has a better
performance than the alone ANFIS network as a
result of genetic optimization. In the second case an
improvement index of 58.2% in position estimation
could be achieved. This fact could also be seen in
the following figures :
7 CONCLUSION
Genetic optimization applied to the adaptive neuro-
fuzzy navigation system. It has been used as a
method to improve the estimation problem .
Obtained results demonstrated the improved
performance of this method over conventional
ANFIS network. Althought the proposed solution
needs more computation effort but it showed
outstanding performance in critical situations such
as satellites’ outages which is much likely in land
navigation. To emphasize on the above advantage,
the number of visible satellites intentionally
degraded to zero during the simulation. The figures
clearly prove the estimation improvement.
REFERENCES
Mackay, D. J. C., 2003. Information theory, inference and
learning algorithms. U.K., Cambridge University
Press.
Farrel, J. A. and Barth, M., 1999. The global positioning
system and inertial navigation. U.S.A, New York:
McGraw-Hill.
Shing, J. and Shang, R., 1993. ANFIS : Adaptive-
Network-based Fuzzy Inference System. IEEE
Transactions on Systems Man and Cybernetics, vol.
23, no. 3, pp. 665-685.
Stroud, P. D., 2001. Kalman-Extended genetic algorithm
for search in nonstationary environments with noisy
fitness evaluations. IEEE Transactions on
Evolutionary Computation, vol. 5, no. 1, pp. 66-77.
Geisler, T., and Manikas, T. W., 2002. Autonomous robot
navigation system using a novel value encoded genetic
algorithm. In Proc. 45th IEEE International Midwest
Symposium on Circuits and Systems, p. 45-48.
Loebis, D., Sutton, R. and Chudley, J., 2003. A fuzzy
kalman filter optimized using a genetic algorithm for
accurate navigation of an autonomous underwater
vehicle. In Proc. MCMC2003 Conference, Girona,
Spain, pp. 19-24.
Simske, S. J., 2003. Navigation using hybrid genetic
programming : initial conditions and state transitions.
HP intelligent enterprise Tech. Lab., Tech. Report,
Palo Alto.
Luke, S. and Spector, L., 1998. A revised comparison of
crossover and mutation in genetic programming. In
Proc. 3th Annual Genetic Programming Conference
(GP98). San Fransisco: Morgan Kaufmann, pp. 208-
213.
Hiliuta, A., Landry, R., Jr. and Gagnon, F., 2004. Fuzzy
correction in a GPS/INS hybrid navigation system.
IEEE Transactions on Aerospace and Electronic
Systems, vol. 40, no. 2, pp. 591-600.
Wang, J. H. and Gao, Y., 2003. Evaluating the accuracy of
GPS positions under severe signal-degradation using
adaptive-network-based fuzzy inference systems
(ANFIS). In the 50th CASI Annual General meeting
and Conference, Canadian Aeronautics and Space
Institute, Montréal, Quebec, Canada.
Mayhew, D. Mc. N. , 1999. Multi-rate sensor fusion for
GPS navigation using kalman filtering. M.S.
thesis,
Dept. Elect. Eng., Virginia Polytech. Institue and State
University, Virginia, USA.
He, X., Chen, Y. and Iz, H. B. , 1998. A reduced-order
model for integrated GPS/INS. IEEE AES Systems
Magazine, pp. 40-45.
Azimi-Sadjadi, B., 2001. Approximate nonlinear filtering
with applications to navigation. Ph.D. dissertation,
Dept. Elect. Eng., Maryland University, College Park.
Fi
g
ure 7: Position error of ANFIS networ
k
Fi
g
ure 8: Position error of o
p
timized ANFIS networ
k
GA BASED DATA FUSION APPROACH IN AN INTELLIGENT INTEGRATED GPS/INS SYSTEM
221
