
LOCAL PATH PLANNING IN UNKNOWN ENVIRONMENT BY
LOCAL 3D ELEVATION MAP CONSTRUCTION
A. Usai and P. Di Giamberardino
Department of Computer and System Sciences ”Antonio Ruberti”
University of Rome ”La Sapienza”
Via Eudossiana 18, 00184 Rome, Italy
Keywords:
Mobile robot, path planning, unknown environment, stereo vision, elevation map.
Abstract:
The paper deals with the problem of computing a path for an autonomous mobile robot, provided by a stere-
ovosion camera, trough obstacles in an unknown environment with rough ground. The planner makes use of a
3D map reporting the presence and the highness of obstacles together with the shape of the ground and its dis-
continuities, under the hypothesis of stationarity. A local solution, with an expanding algorithm, is proposed.
Some experimental results are reported to validate the proposed technique.
1 INTRODUCTION
The path planning problem for autonomous robot
platforms has been a widely investigate problem char-
acterized by several possible approaches depending
on the possible hypothesis on the environment and on
the robot kinematics.
In fact, starting from the simplest problem of a ro-
bot without any kinematic constraints moving in a
perfectly known and static environment, for which a
global path plan for reaching any final goal stating
form any initial position can be performed, for ex-
ample using the Voronoi diagrams approach or tech-
niques based on potential fields among the most fa-
mous approaches, the problem has been more and
more complicated adding one or more of the follow-
ing conditions: i. non stationary environment, i.e.
presence of moving obstacles (like other robots or
humans) or different conditions on some part (like a
door, that can be open or closed); ii. unknown or only
partially known environment, in which the presence
of obstacles (moving or not) or even the possibility
to reach the goal has to be autonomously discovered
by the robot itself; iii. the presence of some con-
straints on the robot motion, like nonholonomic ones
due to the kinematic characteristics of the platforms
(Voronets, 1901).
In the present work, the case of totally unknown en-
vironment and nonholonomic platform with unicycle-
like kinematics is considered. So the problem here
faced is the computation of a path (if any) between
an initial position and a final one for which only the
coordinates are known, without any initial knowledge
on the presence of obstacles or discontinuities in the
ground.
The solution of the problem involves two main as-
pects. The first is the choice of the robot sensors for
the acquisition of the necessary information on the
environment and subsequent analysis; the second is
the strategy for the construction of a feasible path for
reaching the goal.
Regarding the first aspect, the present choice for
the sensors is to use a stereo vision system only. The
hardware used in the present application is a commer-
cial device by Videre Design, the stereo head STH-
MD1. It is composed by two fixed cameras, with
parallel axes, both using CMOS sensible device with
1.3 Megapixels resolution. In the used configuration,
they have two lens whose focus length f is 7.5 mm.
The main advantages of such a choice with respect to
different ones often used, like the rangefinder (Iocchi
et al., 2000) for example, is the absence of physical
interaction with the environment and the similitude
with the human behavior.
As far as the second aspect is concerned, since a
visual system implies that only a part of the field,
the visible part, at a time can be investigated, at each
step of the learning approach only a local knowledge
can be acquired; in addition, without a motion, such
knowledge cannot be increased, since a change in the
point of view is necessary to change the area in the
visible field for investigation. Then, a local path plan-
ner for local motion, based on the construction of a
local and iteratively expanded map, is presented.
On these basis, the first step in the proposed so-
lution is the construction of a suitable map for rep-
403
Usai A. and Di Giamberardino P. (2005).
LOCAL PATH PLANNING IN UNKNOWN ENVIRONMENT BY LOCAL 3D ELEVATION MAP CONSTRUCTION.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics - Robotics and Automation, pages 403-406
DOI: 10.5220/0001167004030406
Copyright
c
SciTePress

resenting the acquired information necessary for the
computation of a feasible path. There are several kind
of maps that can be constructed starting from dis-
tance measurements, depending also from the char-
acteristics of the vision system used. Most of them
work efficiently under the hypothesis of indoor mo-
tion. Among them there are the occupation maps,
where only the position of obstacles are stored, as-
suming to be safe any other position on the ground
(Herbert et al., 1989). But in case of unknown en-
vironment exploration it is not possible to satisfy the
hypothesis of safety for unexplored areas: no regular-
ity assumptions can be posed.
The most suitable kind of maps for the present ap-
plication are the elevation maps, where the known
portion of the environment is represented by the
height of the ground and the objects present. On this
basis, an obstacle is represented by an area whose
height is significantly different from its accessible
neighborhood. Such an information is enough for the
determination of a possible safe path that the mobile
robot can follow, since it can move in all that direc-
tions where the height is equal or a little bit different
(greater or lower) according to the mechanical char-
acteristics of the rover.
The path planning technique here proposed is based
on the construction of an elevation map, according
to the procedure presented in (DiGiamberardino and
Usai, 2005), generated recursively on the basis of con-
tinuous image processing during the robot motion,
which represents the acquired knowledge of the lo-
cal environment in an increasing neighborhood of the
robot.
The paper organization is then the following one.
In section 2 a short description of the technique used
for the construction of the elevation map is given.
Section 3 is devoted to the description of the proce-
dure proposed for the determination of a new connec-
tivity map and, consequently, a local path: in 3.1 the
map construction and in 3.2 the fina path.
2 CONSTRUCTION OF THE
ELEVATION MAP
The basic algorithm adopted for the images analysis
is a disparity map computation starting from a cou-
ple of stereo images. In such an algorithm the cor-
respondence between the couples of conjugate points
in the two images is achieved by means of an area-
based correlation technique. It is well known that this
kind of solution is very efficient for its computational
aspects, but, on the other hand, it does not produce
satisfactory results in presence of discontinuities in
the distances of the objects present in the scene: it
is sufficient that one object is partially covered and
behind another one with respect to the point of view
of the cameras to produce wrong results; in fact, the
correlation of the area including parts of both the ob-
jects at different distances either associates the points
of one object to the other or produces a false object
at an intermediate distance between the two real ones.
Some pre and post elaborations are needed in order to
avoid such errors. In literature some techniques are
proposed ((Murray and Little, 2000),(Fusiello et al.,
2001)) based on a segmentation of the disparity map
in order to manipulate in a different way the sections
that potentially can produce the above described de-
formations. The result is a more clear and realistic
reconstruction with the counterpart in a slower com-
putation. In the present application we propose a dif-
ferent approach based on a standard (and pretty fast)
edge detection algorithm, making use of the addi-
tional information coming from the motion of the ro-
bot and the continuous images acquisition. The accu-
rate description of the algorithm for the construction
of the elevation map and the measures filtering tech-
nic be found in (DiGiamberardino and Usai, 2005). In
figure 4, a VRML model of an outdoor environment
reconstruction is presented.
3 THE PATH PLANNING
PROCEDURE
3.1 Chessboard construction
After the construction of the elevation map, in order to
achieve the planning of a safe path in the environment,
it is necessary to derive a new topological one, gener-
ated starting from the information stored in the eleva-
tion map and combining them with the knowledge of
the mobile robot movement capabilities. Such a map
is called the chessboard. The environment is divided
into cells, storing several informations like the coef-
ficients of the best fit plane, the obstacles presence in
the cell and the fidelity of the elevation measures in
the cell. Figure 5 shows an example of chessboard
using a color code identification with the following
meanings: light gray (green) for free cells with good
measures, dark gray (red) when obstacle are present in
the cell and the measures are good, darkest (blue) for
cells that seems free but the measures are not enough,
lightest (yellow) for apparently occupied cell associ-
ated to poor measures.
It is interesting to see how this coding is done. First
of all, the best fit plane coefficients are computed by
a least square approach. Then it is possible to say if
there is an obstacle for the rover in the cell, compar-
ing the founded fitting plane elevations with the ones
of the true ground trend. In particular, the cell is free
if the difference of the ground elevation and the fitting
ICINCO 2005 - ROBOTICS AND AUTOMATION
404

plane is always smaller than h
max
, that is the height
of the taller obstacle the rover is able to pass (figure
1). Note that a free cell has to be considered occu-
pied if its slope is to high for the rover. Lastly, the
fidelity of the elevation measures in the cell are com-
puted thresholding the veridicity value corresponding
to the measures of the cell.
Figure 1: The cell obstacle detection condition.
Figure 2: The cell connection condition.
Figure 3: Example of an outdoor environment.
3.2 Path planning
After the chessboard is builded, it is possible to derive
from it a connectivity graph, useful for the mobile ro-
bot path planning. In order to reduce the number of
nodes of the graph, grouping similar cells, a third data
structure is derived from the chessboard. Such a struc-
ture is a classical occupancy grid, where the ”pixels”
are marked occupied if:
Figure 4: Example of an outdoor environment reconstruc-
tion.
Figure 5: The Chessboard.
• The corresponding cell in the chessboard is occu-
pied;
• The corresponding cell in the chessboard has not
reliable measures;
• It corresponds to the frontier between two free cells
with a too high difference in height to be passed
by the robot (look at the connection condition in
figure 5).
After this (binary) occupancy map is builded, it
is necessary to augment the founded obstacles ac-
cording to the robot dimensions and filling the possi-
ble ”holes” left by the obstacle augmentation process
(think at those regions that cannot be reacted by any
other cells). In figure 6 it possible to see the planes
approximation concerning a chessboard computed by
the elevation map of an environment with two obsta-
cles. As just noticed, from the chessboard we want to
derive a simpler binary map. In figure 7, it is shown
an example of this data structure. Note how the num-
ber of cells here is less than the one in the chessboard
(figure 8). To divide the configuration space in ”big”
LOCAL PATH PLANNING IN UNKNOWN ENVIRONMENT BY LOCAL 3D ELEVATION MAP CONSTRUCTION
405
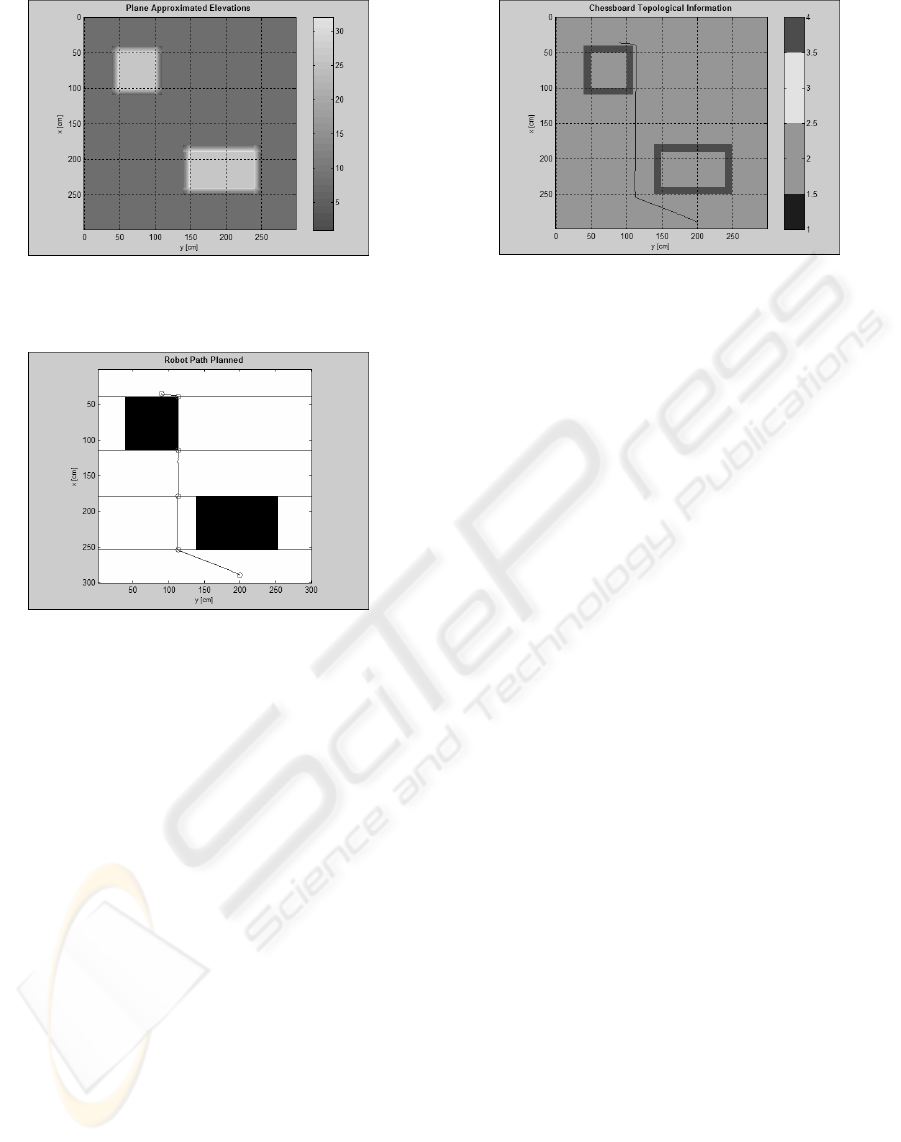
Figure 6: Example of planes approximation for an environ-
ment with two obstacles.
Figure 7: The path planned by the proposed method.
convex cells, the occupancy grid is scanned line by
line and, whenever a ”change in color” is found, a new
horizontal frontier is marked. Once the new cells are
found, a connectivity graph can be used to find which
cells are involved in a specified path from P
start
to
P
goal
. The path is then generated using splines that
connect the border points of each cell. Such points
are choose trying to minimize the distance from the
previous via-point in order to keep the path as short
as possible. In figure 7 and in figure 8, it is possi-
ble to see the planned path in the occupancy grid and
in the chessboard. Note that we are interested in the
exploration of the environment. So, in could be possi-
ble that some areas of the chessboard are unknown (or
better, the measures are not reliable). As noted before,
the not reliable cells (the ones with low veridicity rate)
in the chessboard have to be considered not feasible
for the robot motion. If a planning to a unknown area
is required, the robot will plan until an auxiliary point,
in the known area, is reached and then a new stere-
ohead acquisition is done, pointing the direction of
the desired destination point. The auxiliary point is
chosen in order to stay at the minimum sight distance
(about 50cm, in our configuration) from the frontier
of the unknown area. A new path is then planned from
the actual point to the previously desired one.
Figure 8: The path imposed over the chessboard.
4 CONCLUSION
In this paper a procedure for the determination of a
local map and a feasible path for a robot moving in
an unknown environment is presented. It consists of
two main steps. Some figures show the results of each
step and then the effectiveness of the procedure. Fu-
ture work will focus on the evolution of the proposed
technique for global path planning.
REFERENCES
DiGiamberardino, P. and Usai, A. (2005). Dynamical re-
construction of a 3d elevation map using stereovision
from a mobile robot. In 24th IASTED International
Conference on Modelling, Identification and Control,
pages 398–403.
Fusiello, A., Castellani, U., and Murrino, V. (2001). Relax-
ing symmetric multiple windows stereo using markov
random fields. In Figueiredo, M., Zerubia, J., and Jain,
A., editors, Energy Minimization Methods in Com-
puter Vision and Pattern Recognition, number 2134
in Lecture Notes in Computer Science, pages 91–104.
Spinger.
Herbert, M., Caillas, C., Krotkov, E., Kweon, I., and
Kanade, T. (1989). Terrain mapping for a roving plan-
etary explorer. In ICRA 89, IEEE International Con-
ference on Robotics and Automation, volume 2, pages
997–1002.
Iocchi, L., Konolige, K., and Bajracharya, M. (2000). Vi-
sually realistic mapping of a planar environment with
stereo. In Seventh International Symposium on Exper-
imental Robotics.
Murray, D. and Little, J. (2000). Using real-time stereo vi-
sion for mobile robot navigation. Autonomous Robots,
8(2):161–171.
Voronets, P. (1901). Equation of motion for nonholonomic
systems. Mathematicheskii Sbornik, 22:659–689.
ICINCO 2005 - ROBOTICS AND AUTOMATION
406
