
ROBUST FUZZY CONTROLLER DESIGN FOR UNCERTAIN
DESCRIPTOR MARKOVIAN JUMP SYSTEMS
Wudhichai Assawinchaichote
Department of Electronic and Telecommunication Engineering
King Mongkut’s University of Technology Thonburi, 91 Prachautits Rd., Bangkok 10140, Thailand
Sing Kiong Nguang
Department of Electrical and Computer Engineering
The University of Auckland, Private Bag 92019 Auckland, New Zealand
Keywords:
TS Fuzzy model, H
∞
control, Markovian jumps, LMI.
Abstract:
This paper examines the problem of designing a robust H
∞
state-feedback controller for a class of uncertain
nonlinear descriptor Markovian jump systems described by a Takagi-Sugeno (TS) fuzzy model with Markov-
ian jumps. Based on a linear matrix inequality (LMI) approach, LMI-based sufficient conditions for the un-
certain nonlinear descriptor Markovian jump systems to have an H
∞
performance are derived. The proposed
approach does not involve the separation of states into slow and fast ones and it can be applied not only to
standard, but also to nonstandard nonlinear descriptor systems. A numerical example is provided to illustrate
the design developed in this paper.
1 INTRODUCTION
Markovian jump systems, sometimes called hybrid
systems with a state vector, consists of two compo-
nents; i.e., the state (differential equation) and the
mode (Markov process). The Markovian jump sys-
tem changes abruptly from one mode to another mode
caused by some phenomenon such as environmental
disturbances, changing subsystem interconnections
and fast variations in the operating point of the sys-
tem plant, etc. The switching between modes is gov-
erned by a Markov process with the discrete and finite
state space. Over the past few decades, the Markovian
jump systems have been extensively studied by many
researchers; see (Kushner, 1967; Dynkin, 1965; Won-
ham, 1968; X. Feng and Chizeck, 1992; de Souza and
Fragoso, 1993; Boukas and Liu, 2001; Boukas and
Yang, 1999; Rami and Ghaoui, 1995; Shi and Boukas,
1997). This is due to the fact that jumping systems
have been a subject of the great practical importance.
For the past three decades, descriptor systems
or called singularly perturbed systems have been
intensively studied by many researchers; see (Shi
and Boukas, 1997; K. Benjelloun and Costa, 1997;
E. K. Boukas and Liu, 2001; V. Dragan and Boukas,
1999; Pan and Basar, 1993; Pan and Basar, 1994;
Fridman, 2001; Shi and Dragan, 1999; P. V. Koko-
tovic and O’Reilly, 1986). Singularly perturbed sys-
tems also known as multiple time-scale dynamic sys-
tems normally occur due to the presence of small
“parasitic” parameters, typically small time constants,
masses, etc. In state space, such systems are com-
monly modelled using the mathematical framework
of singular perturbations, with a small parameter, say
ε, determining the degree of separation between the
“slow” and “fast” modes of the system. However, it
is necessary to note that it is possible to solve the sin-
gularly perturbed systems without separating between
slow and fast mode subsystems. But the require-
ment is that the “parasitic” parameters must be large
enough. In the case of having very small “parasitic”
parameters which normally occur in the description
of various physical phenomena, a popular approach
adopted to handle these systems is based on the so-
called reduction technique. According to this tech-
nique the fast variables are replaced by their steady
states obtained with “frozen” slow variables and con-
trols, and the slow dynamics is approximated by the
corresponding reduced order system. This time-scale
is asymptotic, that is, exact in the limit, as the ratio of
the speeds of the slow versus the fast dynamics tends
to zero.
In the last few years, the research on singularly
perturbed systems in the H
∞
sense has been highly
recognized in control area due to the great practical
importance. H
∞
-optimal control of singularly per-
turbed linear systems under either perfect state mea-
surements or imperfect state measurements has been
91
Assawinchaichote W. and Kiong Nguang S. (2005).
ROBUST FUZZY CONTROLLER DESIGN FOR UNCERTAIN DESCRIPTOR MARKOVIAN JUMP SYSTEMS.
In Proceedings of the Second International Conference on Informatics in Control, Automation and Robotics, pages 91-97
DOI: 10.5220/0001156800910097
Copyright
c
SciTePress

investigated via differential game theoretics approach.
Although many researchers have studied the H
∞
con-
trol design of linear singularly perturbed systems for
many years, the H
∞
control design of nonlinear sin-
gularly perturbed systems remains as an open re-
search area. This is due to, in general, nonlinear sin-
gularly perturbed systems can not be decomposed into
slow and fast subsystems.
Recently, a great amount of effort has been made on
the design of fuzzy H
∞
for a class of nonlinear sys-
tems which can be represented by a Takagi-Sugeno
(TS) fuzzy model; see (Nguang and Shi, 2001; Han
and Feng, 1998; B. S. Chen and He, 2001; K. Tanaka
and Wang, 1996). Recent studies (Nguang and Shi,
2001; Han and Feng, 1998; B. S. Chen and He, 2001;
K. Tanaka and Wang, 1996; H. O. Wang and Griffin,
1996) show that a fuzzy model can be used to approx-
imate global behaviors of a highly complex nonlinear
system. In this fuzzy model, local dynamics in differ-
ent state space regions are represented by local linear
systems. The overall model of the system is obtained
by “blending” of these linear models through nonlin-
ear fuzzy membership functions. Unlike conventional
modelling which uses a single model to describe the
global behavior of a system, fuzzy modelling is essen-
tially a multi-model approach in which simple sub-
models (linear models) are combined to describe the
global behavior of the system. Employing the existing
fuzzy results (Nguang and Shi, 2001; Han and Feng,
1998; B. S. Chen and He, 2001; K. Tanaka and Wang,
1996; H. O. Wang and Griffin, 1996) on the singularly
perturbed system, one ends up with a family of ill-
conditioned linear matrix inequalities resulting from
the interaction of slow and fast dynamic modes. In
general, ill-conditioned linear matrix inequalities are
very difficult to solve.
What we intend to do in this paper is to design
a robust H
∞
fuzzy state-feedback controller for a
class of uncertain nonlinear singularly perturbed sys-
tems with Markovian jumps. First, we approximate
this class of uncertain nonlinear singularly perturbed
systems with Markovian jumps by a Takagi-Sugeno
fuzzy model with Markovian jumps. Then based on
an LMI approach, we develop a technique for design-
ing a robust H
∞
fuzzy state-feedback controller such
that the L
2
-gain of the mapping from the exogenous
input noise to the regulated output is less than a pre-
scribed value. To alleviate the ill-conditioned linear
matrix inequalities resulting from the interaction of
slow and fast dynamic modes, these ill-conditioned
LMIs are decomposed into ε-independent LMIs and
ε-dependent LMIs. The ε-independent LMIs are not
ill-conditioned and the ε-dependent LMIs tend to zero
when ε approaches to zero. If ε is sufficiently small,
the original ill-conditioned LMIs are solvable if and
only if the ε-independent LMIs are solvable. The
proposed approach does not involve the separation of
states into slow and fast ones, and it can be applied
not only to standard, but also to nonstandard singu-
larly perturbed systems.
This paper is organized as follows. In Section 2,
system descriptions and definition are presented. In
Section 3, based on an LMI approach, we develop
a technique for designing a robust H
∞
fuzzy state-
feedback controller such that the L
2
-gain of the map-
ping from the exogenous input noise to the regulated
output is less than a prescribed value for the system
described in Section 2. The validity of this approach
is demonstrated by an example from a literature in
Section 4. Finally, conclusions are given in Section 5.
2 SYSTEM DESCRIPTIONS AND
DEFINITIONS
The class of nonlinear uncertain singularly perturbed
system with Markovian jumps under consideration
is described by the following TS fuzzy model with
Markovian jumps:
E
ε
˙x(t) =
P
r
i=1
µ
i
(ν(t))×
h
[A
i
(η(t)) + ∆A
i
(η(t))]x(t)
+[B
1
i
(η(t)) + ∆B
1
i
(η(t))]w(t)
+[B
2
i
(η(t)) + ∆B
2
i
(η(t))]u(t)
i
,
z(t) =
P
r
i=1
µ
i
(ν(t))×
h
[C
1
i
(η(t)) + ∆C
1
i
(η(t))]x(t)
+[D
12
i
(η(t)) + ∆D
12
i
(η(t))]u(t)
i
(1)
where E
ε
=
I 0
0 εI
, ε > 0 is the singular per-
turbation parameter, ν(t) = [ν
1
(t) ··· ν
ϑ
(t)] is
the premise variable that may depend on states in
many cases, µ
i
(ν(t)) denote the normalized time-
varying fuzzy weighting functions for each rule, ϑ
is the number of fuzzy sets, x(t) ∈ ℜ
n
is the
state vector, u(t) ∈ ℜ
m
is the input, w(t) ∈
ℜ
p
is the disturbance which belongs to L
2
[0, ∞),
z(t) ∈ ℜ
s
is the controlled output, the matrix
functions A
i
(η(t)), B
1
i
(η(t)), B
2
i
(η(t)), C
1
i
(η(t)),
D
12
i
(η(t)), ∆A
i
(η(t)), ∆B
1
i
(η(t)), ∆B
2
i
(η(t)),
∆C
1
i
(η(t)) and ∆D
12
i
(η(t)) are of appropriate di-
mensions. {η(t))} is a continuous-time discrete-
state Markov process taking values in a finite set
S = {1, 2, ··· , s} with transition probability matrix
P r
∆
= {P
ık
(t)} given by
P
ık
(t) = P r(η(t + ∆) = k|η(t) = ı)
=
λ
ık
∆ + O(∆) if ı 6= k
1 + λ
ıı
∆ + O(∆) if ı = k
(2)
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
92

where ∆ > 0, and lim
∆−→0
O(∆)
∆
= 0. Here λ
ık
≥ 0
is the transition rate from mode ı (system operating
mode) to mode k (ı 6= k), and
λ
ıı
= −
s
X
k=1,k6=ı
λ
ık
. (3)
For the convenience of notations, we let µ
i
∆
=
µ
i
(ν(t)), η = η(t), and any matrix M (µ, ı)
∆
=
M(µ, η = ı). The matrix functions ∆A
i
(η),
∆B
1
i
(η), ∆B
2
i
(η), ∆C
1
i
(η) and ∆D
12
i
(η) repre-
sent the time-varying uncertainties in the system and
satisfy the following assumption.
Assumption 1
∆A
i
(η) = F (x(t), η, t)H
1
i
(η),
∆B
1
i
(η) = F (x(t), η, t)H
2
i
(η),
∆B
2
i
(η) = F (x(t), η, t)H
3
i
(η),
∆C
1
i
(η) = F (x(t), η, t)H
4
i
(η),
and ∆D
12
i
(η) = F (x(t), η, t)H
5
i
(η),
where H
j
i
(η), j = 1, 2, ··· , 5 are known matri-
ces which characterize the structure of the uncertain-
ties. Furthermore, there exists a positive function
ρ(η) such that the following inequality holds:
kF (x(t), η, t)k ≤ ρ(η). (4)
We recall the following definition.
Definition 1 Suppose γ is a given positive number. A
system of the form (1) is said to have the L
2
-gain less
than or equal to γ if
E
"
Z
T
f
0
{z
T
(t)z(t) −γ
2
w
T
(t)w (t)} dt
#
≤ 0, (5)
where x(0) = 0 and E [·] stands for the mathematical
expectation, for all T
f
and all w(t) ∈ L
2
[0, T
f
].
Note that for the symmetric block matrices, we use
(∗) as an ellipsis for terms that are induced by sym-
metry.
3 ROBUST H
∞
FUZZY
STATE-FEEDBACK CONTROL
DESIGN
This section provides the LMI-based solutions to
the problem of designing a robust H
∞
fuzzy state-
feedback controller that guarantees the L
2
-gain of the
mapping from the exogenous input noise to the regu-
lated output to be less than some prescribed value.
First, we consider the following H
∞
fuzzy state-
feedback which is inferred as the weighted average of
the local models of the form:
u(t) =
r
X
j=1
µ
j
K
j
(ı)x(t). (6)
Then, we describe the problem under our study as
follows.
Problem Formulation: Given a prescribed H
∞
per-
formance γ > 0, design a robust H
∞
fuzzy state-
feedback controller of the form (6) such that the in-
equality (5) holds.
Before presenting our first main result, we recall
the following lemma.
Lemma 1 Consider the system (1). Given a pre-
scribed H
∞
performance γ > 0, for ı = 1, 2, ··· , s,
if there exist matrices P
ε
(ı) = P
T
ε
(ı), positive con-
stants δ(ı) and matrices Y
j
(ı), j = 1, 2, ··· , r such
that the following ε-dependent linear matrix inequal-
ities hold:
P
ε
(ı) > 0 (7)
Ψ
ii
(ı, ε) < 0, i = 1, 2, ··· , r(8)
Ψ
ij
(ı, ε) + Ψ
ji
(ı, ε) < 0, i < j ≤ r (9)
where
Ψ
ij
(ı, ε) =
Φ
ij
(ı, ε) (∗)
T
(∗)
T
(∗)
T
R(ı)
˜
B
T
1
i
(ı) −γR(ı) (∗)
T
(∗)
T
Υ
ij
(ı, ε) 0 −γR(ı) (∗)
T
Z
T
(ı, ε) 0 0 −P(ı, ε)
Φ
ij
(ı, ε) = A
i
(ı)E
−1
ε
P
ε
(ı) + E
−1
ε
P
ε
(ı)A
T
i
(ı)
+B
2
i
(ı)Y
j
(ı) + Y
T
j
(ı)B
T
2
i
(ı)
+λ
ıı
E
−1
ε
P
ε
(ı),
Υ
ij
(ı, ε) =
˜
C
1
i
(ı)E
−1
ε
P
ε
(ı) +
˜
D
12
i
(ı)Y
j
(ı),
R(ı) = diag {δ(ı)I, I, δ(ı)I, I},
Z(ı, ε) =
p
λ
ı1
E
−1
ε
P
ε
(ı) ···
q
λ
ı(ı−1)
E
−1
ε
P
ε
(ı)
q
λ
ı(ı+1)
E
−1
ε
P
ε
(ı) ···
p
λ
ıs
E
−1
ε
P
ε
(ı)
,
P(ı, ε) = diag
n
E
−1
ε
P
ε
(1), ··· , E
−1
ε
P
ε
(ı − 1),
E
−1
ε
P
ε
(ı + 1), ··· , E
−1
ε
P
ε
(s)
o
,
ROBUST FUZZY CONTROLLER DESIGN FOR UNCERTAIN DESCRIPTOR MARKOVIAN JUMP SYSTEMS
93

with
˜
B
1
i
(ı) = [
I I I B
1
i
(ı)
]
˜
C
1
i
(ı) =
h
γρ(ı)H
T
1
i
(ı)
√
2ℵ(ı)ρ(ı)H
T
4
i
(ı)
0
√
2ℵ(ı)C
T
1
i
(ı)
i
T
˜
D
12
i
(ı) =
h
0
√
2ℵ(ı)ρ(ı)H
T
5
i
(ı)
γρ(ı)H
T
3
i
(ı)
√
2ℵ(ı)D
T
12
i
(ı)
i
T
ℵ(ı) =
I + ρ
2
(ı)
r
X
i=1
r
X
j=1
h
kH
T
2
i
(ı)H
2
j
(ı)k
i
1
2
then the inequality (5) holds. Furthermore, a suitable
choice of the fuzzy controller is
u(t) =
r
X
j=1
µ
j
K
ε
j
(ı)x(t) (10)
where
K
ε
j
(ı) = Y
j
(ı)(P
ε
(ı))
−1
E
ε
. (11)
Proof: The desired result can be carried out by a
similar technique used in (D. P. de Farias and Costa,
2000), (Nguang and Shi, 2003), and (Nguang and Shi,
2001). Due to limited pages, the detail of the proof is
omitted for brevity.
Remark 1 The linear matrix inequalities given in
Lemma 1 becomes ill-conditioned when ε is suffi-
ciently small, which is always the case for the sin-
gularly perturbed system. In general, these ill-
conditioned linear matrix inequalities are very diffi-
cult to solve. Thus, to alleviate these ill-conditioned
linear matrix inequalities, we have the following the-
orem which does not depend on ε.
Now we are in the position to present our first re-
sult.
Theorem 1 Consider the system (1). Given a pre-
scribed H
∞
performance γ > 0, for ı = 1, 2, ··· , s,
if there exist matrices P (ı), positive constants δ(ı)
and matrices Y
j
(ı), j = 1, 2, ··· , r such that the fol-
lowing ε-independent linear matrix inequalities hold:
EP (ı) + P (ı)D > 0 (12)
Ψ
ii
(ı) < 0, i = 1, 2, ··· , r (13)
Ψ
ij
(ı) + Ψ
ji
(ı) < 0, i < j ≤ r (14)
where EP (ı) = P
T
(ı)E, P (ı)D = DP
T
(ı), E =
I 0
0 0
, D =
0 0
0 I
,
Ψ
ij
(ı) =
Φ
ij
(ı) (∗)
T
(∗)
T
(∗)
T
R(ı)
˜
B
T
1
i
(ı) −γR(ı) (∗)
T
(∗)
T
Υ
ij
(ı) 0 −γR(ı) (∗)
T
Z
T
(ı) 0 0 −P(ı)
Φ
ij
(ı) = A
i
(ı)P (ı) + P
T
(ı)A
T
i
(ı) + B
2
i
(ı)Y
j
(ı)
+Y
T
j
(ı)B
T
2
i
(ı) + λ
ıı
˜
¯
P (ı),
Υ
ij
(ı) =
˜
C
1
i
(ı)P (ı) +
˜
D
12
i
(ı)Y
j
(ı),
R(ı) = diag{δ(ı)I, I, δ(ı)I, I},
Z(ı) =
p
λ
ı1
˜
¯
P (ı) ···
q
λ
ı(ı−1)
˜
¯
P (ı)
q
λ
ı(ı+1)
˜
¯
P (ı) ···
p
λ
ıs
˜
¯
P (ı)
,
P(ı) = diag
n
˜
¯
P (1), ··· ,
˜
¯
P (ı −1),
˜
¯
P (ı + 1), ··· ,
˜
¯
P (s)
o
,
˜
¯
P (ı) =
P (ı) + P
T
(ı)
2
with
˜
B
1
i
(ı) = [
I I I B
1
i
(ı)
]
˜
C
1
i
(ı) =
h
γρ(ı)H
T
1
i
(ı)
√
2ℵ(ı)ρ(ı)H
T
4
i
(ı)
0
√
2ℵ(ı)C
T
1
i
(ı)
i
T
˜
D
12
i
(ı) =
h
0
√
2ℵ(ı)ρ(ı)H
T
5
i
(ı)
γρ(ı)H
T
3
i
(ı)
√
2ℵ(ı)D
T
12
i
(ı)
i
T
ℵ(ı) =
I + ρ
2
(ı)
r
X
i=1
r
X
j=1
h
kH
T
2
i
(ı)H
2
j
(ı)k
i
1
2
then there exists a sufficiently small ˆε > 0 such that
the inequality (5) holds for ε ∈ (0, ˆε]. Furthermore, a
suitable choice of the fuzzy controller is
u(t) =
r
X
i=1
µ
j
K
j
(ı)x(t) (15)
where
K
j
(ı) = Y
j
(ı)(P (ı))
−1
. (16)
Proof: Due to limited pages, the detail of the proof
is omitted for brevity.
4 ILLUSTRATIVE EXAMPLE
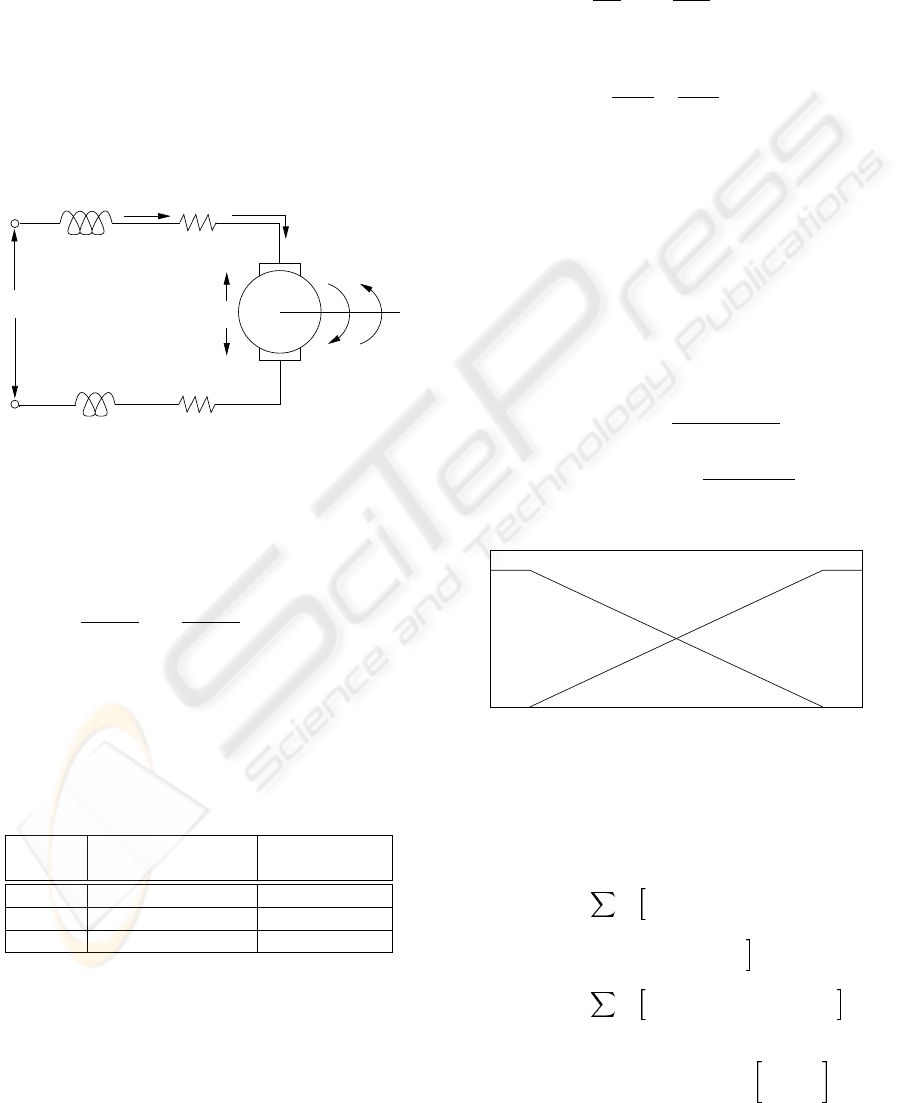
Consider a modified series dc motor model based on
(Mehta and Chiasson, 1998) as shown in Fig. 1 which
is governed by the following difference equations:
J
d˜ω(t)
dt
= K
m
L
f
˜
i
2
(t) − (D + ∆D)˜ω(t)
L
d
˜
i(t)
dt
= −R
˜
i(t) − K
m
L
f
˜
i(t)˜ω(t) +
˜
V (t)
(17)
where ˜ω(t) = ω(t) − ω
ref
(t) is the deviation of
the actual angular velocity from the desired angular
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
94
velocity,
˜
i(t) = i(t) − i
ref
(t) is the deviation of
the actual current from the desired current,
˜
V (t) =
V (t) − V
ref
(t) is the deviation of the actual input
voltage from the desired input voltage, J is the mo-
ment of inertia, K
m
is the torque/back emf constant,
D is the viscous friction coefficient, and R
a
, R
f
, L
a
and L
f
are the armature resistance, the field wind-
ing resistance, the armature inductance and the field
winding inductance, respectively, with R
∆
= R
f
+ R
a
and L
∆
= L
f
+ L
a
. Note that in a typical series-
connected dc motor, the condition L
f
≫ L
a
holds.
When one obtains a series-connected dc motor, we
have i(t) = i
a
(t) = i
f
(t). Now let us assume that
|∆J| ≤ 0.1J.
b
V
L
I
f
I
a
V
+
−
back emf
f
a
L
a
R
f
R
+
−
Dω
τ
Figure 1: A modified series dc motor equivalent circuit.
Giving x
1
(t) = ˜ω(t), x
2
(t) =
˜
i(t) and u(t) =
˜
V (t), (17) becomes
˙x
1
(t)
ε ˙x
2
(t)
=
−
D
(J+∆J)
K
m
L
f
(J+∆J)
x
2
(t)
−K
m
L
f
x
2
(t) −R
x
1
(t)
x
2
(t)
+
0
1
u(t) (18)
where ε = L represents a small parasitic parameter.
Assume that, the system is aggregated into 3 modes
as shown in Table 1:
Table 1: System Terminology.
Mode ı Moment of Inertia J(ı) ± ∆J(ı)
(kg·m
2
)
1 Small 0.0005 ±10%
2 Normal 0.005 ±10%
3 Large 0.05 ±10%
The transition probability matrix that relates the
three operation modes is given as follows:
P
ık
=
"
0.67 0.17 0.16
0.30 0.47 0.23
0.26 0.10 0.64
#
.
The parameters for the system are given as R =
10 Ω, L
f
= 0.005 H, D = 0.05 N·m/rad/s and K
m
=
1 N·m/A. Substituting the parameters into (18), we
get
˙x
1
(t)
ε ˙x
2
(t)
=
−
0.05
J(ı)
0.005
J(ı)
x
2
(t)
−0.005x
2
(t) −10
x
1
(t)
x
2
(t)
+
0 0
0.1 0
w(t) +
0
1
u(t)
+
−
0.05
∆J(ı)
0.005
∆J(ı)
x
2
(t)
0 0
x
1
(t)
x
2
(t)
z(t) =
1 0
0 1
x
1
(t)
x
2
(t)
+
0
1
u(t)
where x(t) = [x
T
1
(t) x
T
2
(t)]
T
is the state variables,
w(t) = [w
T
1
(t) w
T
2
(t)]
T
is the disturbance input,
u(t) is the controlled input and z(t) is the controlled
output.
The control objective is to control the state variable
x
2
(t) for the range x
2
(t) ∈ [N
1
N
2
]. For the sake of
simplicity, we will use as few rules as possible. Note
that Fig. 2 shows the plot of the membership function
represented by
M
1
(x
2
(t)) =
−x
2
(t) + N
2
N
2
− N
1
and M
2
(x
2
(t)) =
x
2
(t) − N
1
N
2
− N
1
.
Knowing that x
2
(t) ∈ [N
1
N
2
], the nonlinear system
1 2
1
0
M (x ) M (x )
N
2
1
N
x (t)
2
2 2
−3
3
0
Figure 2: Membership functions for the two fuzzy set.
(19) can be approximated by the following TS fuzzy
model
E
ε
˙x(t) =
r
i=1
µ
i
[A
i
(ı) + ∆A
i
(ı)]x(t)
+B
1
i
(ı)w(t) + B
2
i
(ı)u(t)
, x(0) = 0,
z(t) =
r
i=1
µ
i
C
1
i
(ı)x(t) + D
12
i
(ı)u(t)
,
where µ
i
is the normalized time-varying fuzzy weighting
functions for each rule, i = 1, 2, x(t) =
x
1
(t)
x
2
(t)
, E
ε
=
ROBUST FUZZY CONTROLLER DESIGN FOR UNCERTAIN DESCRIPTOR MARKOVIAN JUMP SYSTEMS
95

1 0
0 ε
, ∆A
1
(ı) = F (x(t), ı, t)H
1
1
(ı), ∆A
2
(ı) =
F (x(t), ı, t)H
1
2
(ı),
A
1
(1) =
−100 10N
1
−0.005N
1
−10
,
A
2
(1) =
−100 10N
2
−0.005N
2
−10
,
A
1
(2) =
−10 N
1
−0.005N
1
−10
,
A
2
(2) =
−10 N
2
−0.005N
2
−10
,
A
1
(3) =
−1 0.1N
1
−0.005N
1
−10
,
A
2
(3) =
−1 0.1N
2
−0.005N
2
−10
,
B
1
1
(ı) = B
1
2
(ı) =
0 0
0.1 0
,
B
2
1
(ı) = B
2
2
(ı) =
0
1
,
C
1
1
(ı) = C
1
2
(ı) =
1 0
0 1
,
and D
12
1
(ı) = D
12
2
(ı) =
0
1
,
with kF (x(t), ı, t)k ≤ 1. Then we have
H
1
1
(ı) =
−
0.05
J (ı)
0.05
J (ı)
N
1
0 0
and H
1
2
(ı) =
−
0.05
J (ı)
0.05
J (ı)
N
2
0 0
.
In this simulation, we select N
1
= −3 and N
2
= 3.
Using the LMI optimization algorithm and Theorem 1
with ε = 0.005, γ = 1 and δ(1) = δ(2) = δ(3) = 1,
we obtain the results given in Fig. 3 and Fig. 4.
Remark 2 Employing results given in (Nguang and
Shi, 2001; Han and Feng, 1998; B. S. Chen and He,
2001; K. Tanaka and Wang, 1996; H. O. Wang and
Griffin, 1996) and Matlab LMI solver (S. Boyd and
Balakrishnan, 1994), it is easy to realize that when
ε < 0.005 for the state-feedback control design, LMIs
become ill-conditioned and Matlab LMI solver yields
an error message, “Rank Deficient”. However, the
state-feedback fuzzy controller proposed in this paper
guarantee that the inequality (5) holds for the sys-
tem (19). Fig. 3 shows the result of the changing
between modes during the simulation with the initial
mode at mode 1 and ε = 0.005. The disturbance in-
put signal, w(t), which was used during simulation
is with magnitude 0.1 and frequency 1 Hz. The ra-
tio of the regulated output energy to the disturbance
input noise energy obtained by using the H
∞
fuzzy
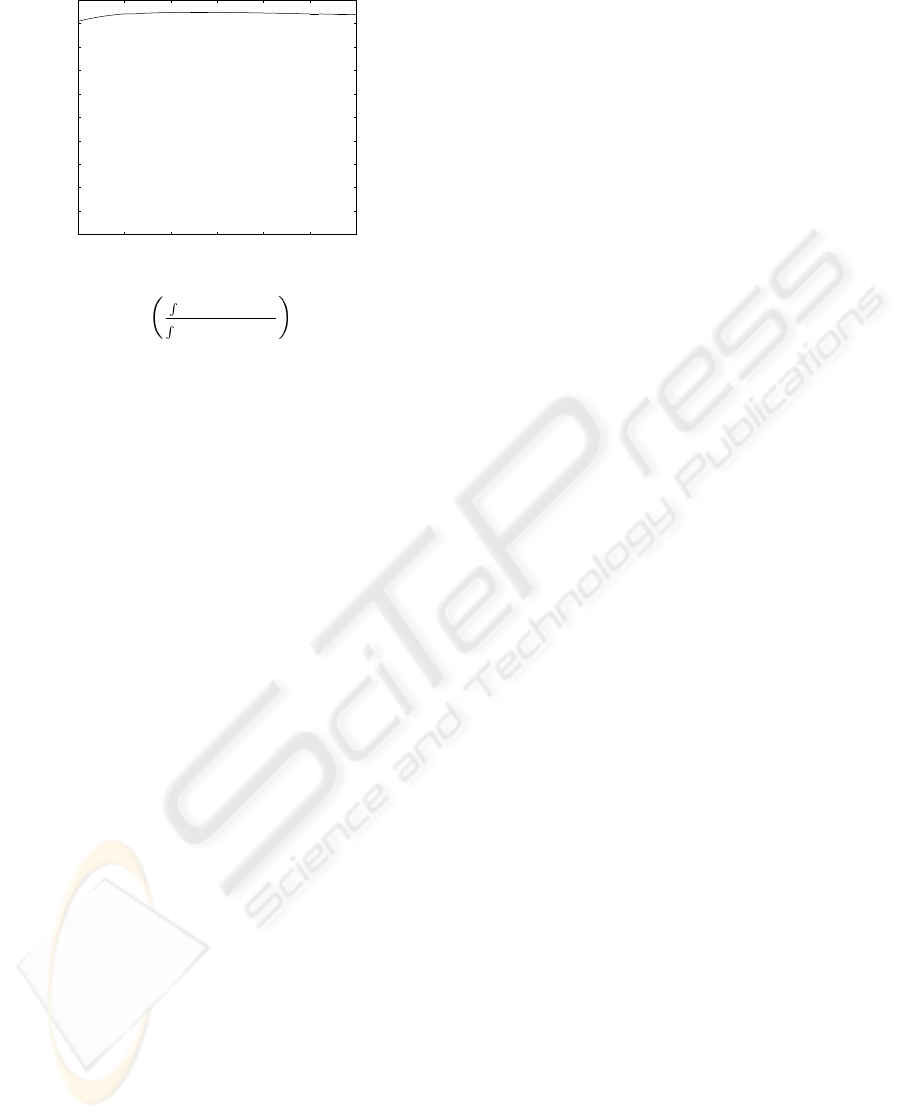
controller is depicted in Fig. 4. The ratio of the regu-
lated output energy to the disturbance input noise en-
ergy tends to a constant value which is about 0.0094.
So γ =
√
0.0094 = 0.0970 which is less than the
prescribed value 1. Finally, Table 2 shows the perfor-
mance index, γ, for different values of ε.
5 CONCLUSION
This paper has investigated the problem of design-
ing a robust H
∞
fuzzy state-feedback controller for
a class of uncertainty Markovian jump nonlinear sin-
gularly perturbed systems that guarantees the L
2
-gain
from an exogenous input to a regulated output to be
less or equal to a prescribed value. First, we approx-
imate this class of uncertain Markovian jump non-
linear singularly perturbed systems by a class of un-
certain Takagi-Sugeno fuzzy models with Markov-
ian jumps. Then, based on an LMI approach, LMI-
based sufficient conditions for the uncertain Markov-
ian jump nonlinear singularly perturbed systems to
have an H
∞
performance are derived. The proposed
approach does not involve the separation of states into
slow and fast ones and it can be applied not only to
standard, but also to nonstandard nonlinear singularly
perturbed systems. An illustrative example is used
to illustrate the effectiveness of the proposed design
techniques.
Table 2: The performance index γ for different values of ε.
The performance index γ
ε State-feedback control design
0.005 0.0970
0.10 0.4796
0.30 0.8660
0.40 0.9945
0.41 > 1
0 0.5 1 1.5 2 2.5 3
1
1.5
2
2.5
3
Mode
Time (sec)
Figure 3: The result of the changing between modes during
the simulation with the initial mode at mode 1.
ICINCO 2005 - INTELLIGENT CONTROL SYSTEMS AND OPTIMIZATION
96
0 0.5 1 1.5 2 2.5 3
0
0.001
0.002
0.003
0.004
0.005
0.006
0.007
0.008
0.009
0.01
Ratio of the regulated output energy to the disturbance energy
Time (sec)
Figure 4: The ratio of the regulated output energy to the dis-
turbance noise energy,
T
f
0
z
T
(t)z(t)dt
T
f
0
w
T
(t)w(t)dt
with ε = 0.005.
REFERENCES
B. S. Chen, C. S. T. and He, Y. Y. (2001). Mixed H
2
/H
∞
fuzzy output feedback control design for nonlinear dy-
namic systems: An lmi approach. IEEE Trans. Fuzzy
Syst., 8:249–265.
Boukas, E. K. and Liu, Z. K. (2001). Suboptimal design of
regulators for jump linear system with time-multiplied
quadratic cost. IEEE Tran. Automat. Contr., 46:944–
949.
Boukas, E. K. and Yang, H. (1999). Exponential stabiliz-
ability of stochastic systems with markovian jump pa-
rameters. Automatica, 35:1437–1441.
D. P. de Farias, J. C. Geromel, J. B. R. d. V. and Costa,
O. L. V. (2000). Output feedback control of markov
jump linear systems in continuous-time. IEEE Trans.
Automat. Contr., 45:944–949.
de Souza, C. E. and Fragoso, M. D. (1993). H
∞
control
for linear systems with markovian jumping parame-
ters. Control-Theory and Advanced Tech., 9:457–466.
Dynkin, E. B. (1965). Markov Process. Springer-Verlag,
Berlin.
E. K. Boukas, Z. K. L. and Liu, G. X. (2001). Delay-
dependent robust stability and H
∞
control of jump
linear systems with time-delay. Int. J. of Contr.
Fridman, E. (2001). State-feedback H
∞
control of nonlin-
ear singularly perturbed systems. Int. J. Robust Non-
linear Contr., 6:25–45.
H. O. Wang, K. T. and Griffin, M. F. (1996). An approach
to fuzzy control of nonlinear systems: Stability and
design issues. IEEE Trans. Fuzzy Syst., 4:14–23.
Han, Z. X. and Feng, G. (1998). State-feedback H
∞
con-
troller design of fuzzy dynamic system using lmi tech-
niques. In Fuzzy-IEEE’98, pages 538–544.
K. Benjelloun, E. K. B. and Costa, O. L. V. (1997). H
∞
control for linear time delay with markovian jumping
parameters. J. of Opt. Theory and App., 105:73–95.
K. Tanaka, T. I. and Wang, H. O. (1996). Robust stabi-
lization of a class of uncertain nonlinear systems via
fuzzy control: Quadratic stability, H
∞
control theory,
and linear martix inequality. IEEE Trans. Fuzzy Syst.,
4:1–13.
Kushner, H. J. (1967). Stochastic Stability and Control.
Academic Press, New York.
Mehta, S. and Chiasson, J. (1998). Nonlinear control of a
series dc motor: Theory and experiment. EEE Trans.
Ind. Electron., 45:134–141.
Nguang, S. K. and Shi, P. (2001). H
∞
fuzzy output feed-
back control design for nonlinear systems: An lmi
approach. In Proc. IEEE Conf. Decision and Contr.,
pages 4352–4357.
Nguang, S. K. and Shi, P. (2003). H
∞
fuzzy output feed-
back control design for nonlinear systems: An lmi ap-
proach. IEEE Trans. Fuzzy Syst., 11:331–340.
P. V. Kokotovic, H. K. K. and O’Reilly, J. (1986). Singular
Perturbation Methods in Control: Analysis and De-
sign. Academic Press, London.
Pan, Z. and Basar, T. (1993). H
∞
–optimal control for sin-
gularly perturbed systems part i: Perfect state mea-
surements. Automatica, 29:401–423.
Pan, Z. and Basar, T. (1994). H
∞
–optimal control for sin-
gularly perturbed systems part ii: Imperfect state mea-
surements. IEEE Trans. Automat. Contr., 39:280–299.
Rami, M. A. and Ghaoui, L. E. (1995). H
∞
state-feedback
control of jump linear systems. In Proc. Conf. Deci-
sion and Contr., pages 951–952.
S. Boyd, L. El Ghaoui, E. F. and Balakrishnan, V. (1994).
Linear Matrix Inequalities in Systems and Control
Theory. SIAM, Philadelphia.
Shi, P. and Boukas, E. K. (1997). H
∞
control for markovian
jumping linear system with parametric uncertainty. J.
of Opt. Theory and App., 95:75–99.
Shi, P. and Dragan, V. (1999). Asymptotic H
∞
control
of singularly perturbed system with parametric uncer-
tainties. Int. J. Robust NonlinearIEEE Trans. Automat.
Contr., 44:1738–1742.
V. Dragan, P. S. and Boukas, E. K. (1999). Control of singu-
larly perturbed system with markovian jump parame-
ters: An H
∞
approach. Automatica, 35:1369–1378.
Wonham, W. M. (1968). On a matrix riccati equation of
stochastic control. SIAM J. Contr., 6:681–697.
X. Feng, K. A. Loparo, Y. J. and Chizeck, H. J. (1992).
Stochastic stability properties of jump linear system.
IEEE Tran. Automat. Contr., 37:38–53.
ROBUST FUZZY CONTROLLER DESIGN FOR UNCERTAIN DESCRIPTOR MARKOVIAN JUMP SYSTEMS
97
